基于自抗扰控制技术开关磁阻电机转矩脉动抑制研究

李华柏，莫 坚，李建忠

(湖南铁道职业技术学院，湖南 株洲 412001)

0 引 言

开关磁阻电机(简称SR电机)结构简单、效率高、控制方式灵活多样、调速性能优良。但是SR电机的双凸极结构使得它的转矩脉动比其它类型电机更加突出，从而限制了它的应用范围与发展。大量分析和研究表明，SR电机的转矩脉动与噪音主要是作用于定子上的脉动径向力导致[1-3]。

1 SR电机转矩脉动原因分析

1.1 SR电机径向力分析

图1为气隙磁导计算结构图，将广义坐标x取作电机径向坐标g，由文献[1]可知，则fem就是电机的径向力fr[2-3]

(1)

(2)

(3)

气隙磁导为

λ=lefpμ0

(4)

式中，φ为气隙磁通，Um为气隙磁动势，λ为气隙磁导，lef为气隙轴向有效长度，p为气隙比磁导，μ0为空气磁导率。

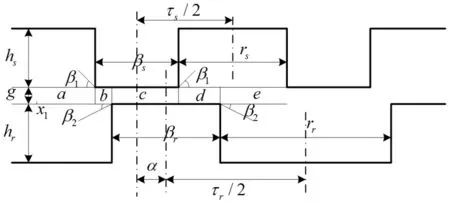
图1 气隙磁导计算图

βs、βr为定、转子极弧，g为气隙长度，N为匝数。β1与β2分别为定子磁极、转子磁极两侧倾角；α为定子极轴、转子极轴夹角[1-2]。

β1和β2与极弧的关系为

(5)

(6)

(7)

可求得径向力：

(8)

式(8)表明，SR电机的径向力受多个参数的综合影响，与绕组匝数、相电流、铁心轴向长度成正比，与气隙长度的平方近似成反比，且与电机定、转子极弧等都有一定的关系[1]。

1.2 SR电机转矩脉动分析

SR电机运行时，定子q相绕组轮流导通一次后，平均电磁转矩可表示为

(9)

(10)

SR电机的电磁转矩与电磁力与磁通密度直接相关。图2是基于Ansoft 分析得到的SR电机磁通密度矢量分布图，可见SR电机通电磁极下定子极和转子极相对的气隙单元磁通畸变较为严重；磁通密度分布明显不均匀[1,4]。磁通的畸变与密度分布不均会影响转矩的脉动。

图2 12/8极 SR电机磁通密度矢量分布图

图3为采用Ansoft 计算而得到的力矩与转矩波形。可见瞬时转矩随电磁力的增大而增大。

图3 12/8极SR电机力矩和转矩波形

由上述分析可知：SR电机的转矩脉动可以从优化电机结构尺寸参数及采用适当的控制策略两方面进行控制。

2 SR电机自抗扰控制系统设计

2.1 SR电机直接转矩控制原理

忽略绕组电阻，SR电机电磁转矩也可表达为

(11)

式中，θ为转子位置角，i为相电流。由式(11)可知，保持定子磁链幅值不变，当ψ超前于θ时，Te增加；当ψ滞后于θ时，Te减小。SR电机直接转矩控制就是通过控制定子磁链超前或滞后于转子位置角，使转矩脉动最小化[3]。

ψ(k)=ψ(k-1)+U(k)Ts

(12)

式中，Ts为采样周期，其矢量关系如图2所示。

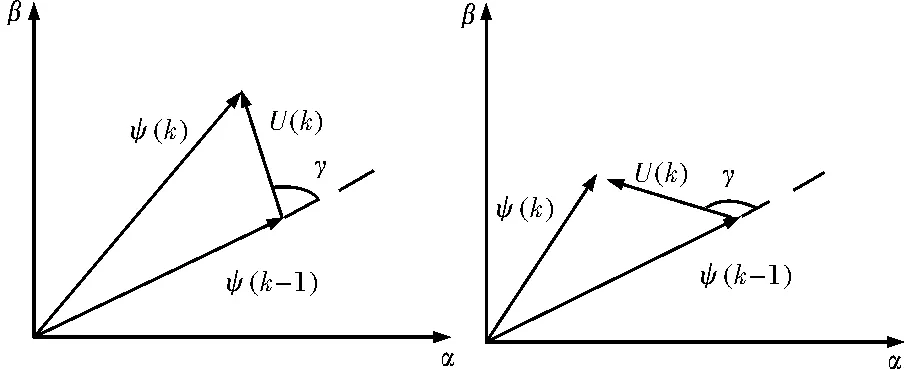
图4 定子磁链与电压矢量的关系

图中，U(k)为电压矢量，γ为U(k)与ψ(k)之间夹角。当|γ|<90°时，电压矢量施加使磁链幅值增加。当|γ|>90°时，电压矢量施加后使磁链幅值减小。

基于直接转矩控制的SR电机控制如图5所示。瞬时电磁转矩T、瞬时磁链ψ将分别与给定值T*、ψ*进行比较，滞环比较器根据转矩和磁链的变化要求调节开关角，将转矩脉动限制在一定的范围内，降低转矩脉动[3]。

图5 基于直接转矩控制的SR电机控制框图

2.2 自抗扰控制器结构

直接转矩控制虽然能较好地抑制转矩脉动，但由于SR电机的非线性、较强的时变性，直接转矩的PID控制方式就无法达到高性能指标。因此本文采用自抗扰控制技术对转速与转矩脉动进行精确控制。

基于自抗扰控制的转矩控制技术(简称ADRC)通过实时估计出系统所受的总扰动，并及时予以补偿来抑制电机的转矩脉动。自抗扰控制器由跟踪微分器TD 、扩张状态观测器ESO、非线性状态误差反馈NLSEF和扰动补偿组成[5-7]。二阶ADRC控制系统如图6所示。

图6中，v为控制量的给定值，v1是v的跟踪信号，v2是v的近似微分信号，u是控制量。y为输出实际值，z1为y的观测值，z2为总扰动z3的估计值，z3为总扰动的观测值，b0为控制量增益b的估计值，e1、e2分别为系统的状态误差。

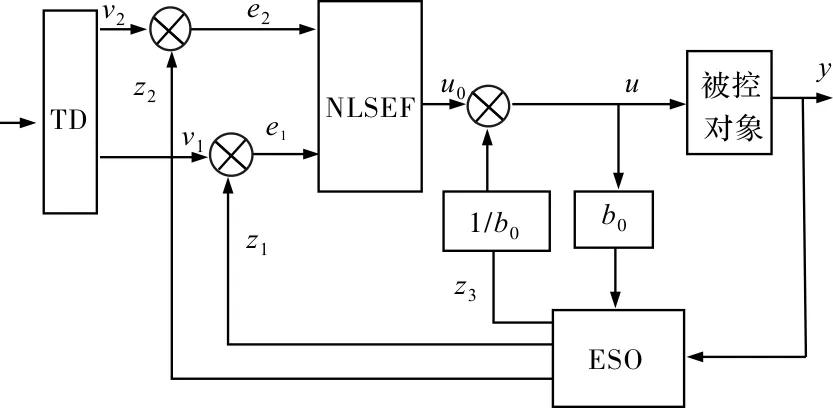
图6 二阶自抗扰控制器结构

2.3 基于ADRC的SR电机转速控制器设计

SR电机ADRC转速、转矩控制系统结构如图7所示。

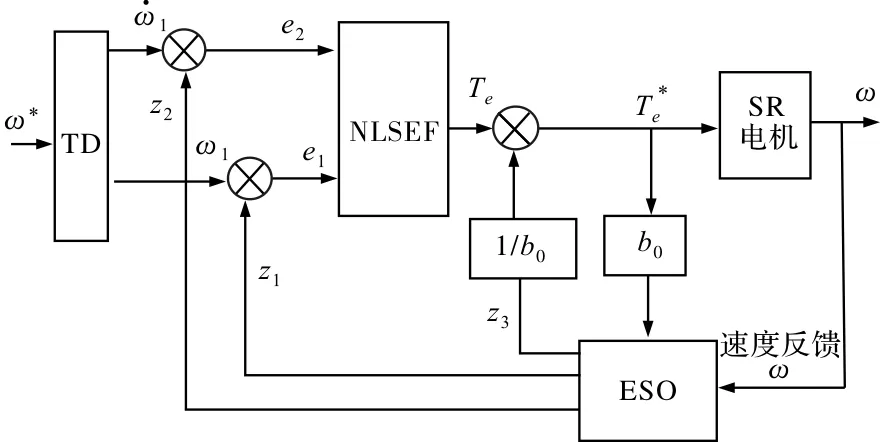
图7 SR电机ADRC自抗扰控制系统

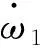
SR电机的机械运动方程为

(13)

式中,J为SR电机的转动惯量，ω为转子角速度，Te为电磁转矩，TL为负载转矩，D为阻尼系数。

(14)

式(14)表明，SR电机的转速受转动惯量、负载转矩与阻尼系数的影响。系统所受内外扰动总和z3(t)包括转动惯量的变化(内部扰动)与将负载转矩与阻尼系数变化(外部扰动)[8]。故式(14)可以表示为

(15)

一阶跟踪微分器数学模型设计如下：

(16)

以电机的实际转速ω为输入信号，通过二阶ESO处理后，得到实际转速的观测值z1和总扰动估计值z2[8]。扩张状态观测器ESO的方程为

(17)

式中，η1与η2为反馈增益，b0为补偿因子。fal为非线性函数，u为控制量。e为输入误差信号，ε为滤波因数，取0.5，δ表示线性区间的宽度。

(18)

TD方程为

(19)

其中，sgn为符号函数。

NLSEF方程为

(20)

式中，k1,k2为可调参数。

再由ESO实时估计出的扰动z3进行补偿，得到转矩扰动观测值，即输出控制量为

(21)

3 仿真分析

SR电机ADRC控制系统仿真流程如图8所示。

图8 基于ADRC速度调节器流程图

当SR电机空载起动，给定转速为1500 r/min，负载转矩0.5s时突加至12 Nm，1.5s时突卸至6Nm。分别采用PI控制、滑模变结构控制和自抗扰控制时，转速波形如图9所示，转矩波形如图10所示。

图9 转速跟踪波形

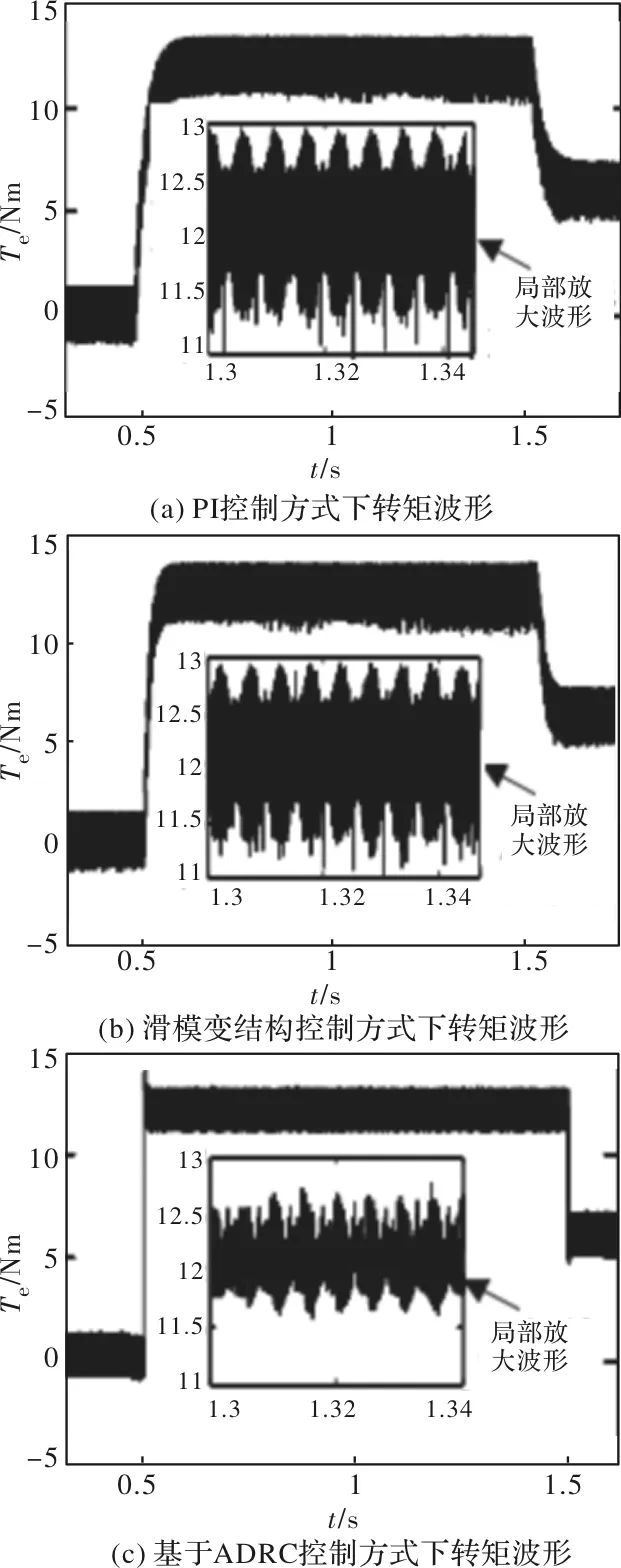
图10 负载变化时转矩波形

图9表明，三种控制方式下，SR电机空载起动时经过约0.1s左右就达到了给定转速，响应均较快。在0.5s负载转矩突然增加时，PI调节方式下转速下降了40%左右，经过1.2s左右恢复到给定转速；滑模变结构调节方式下转速下降了20%左右，经过1.1s左右恢复到给定转速。而采用ADRC调节，转速仅略有下降，经过0.02s迅速回到稳态。突卸负载时的转速的情况与突加负载类似[5]。

因此，三种控制方式下，ADRC相比于PI调节和滑模变结构控制，动态响应最快、抗干扰能力最强。

对比图10(a), 图10(b),图10(c)可知，在突加负载和突减负载的情况下，三种控制方式下，采用自抗扰控制时转矩响应最快，但是在负载突变时，转矩波形出现了尖峰。滑模变结构控制和PI控制，转矩响应较慢，但是是转矩波形相对比较平稳。

从图10 局部放大波形中可以看出，给定负载转矩为12 Nm时，采用ADRC控制方案时转矩脉动范围是11.7～2.5 Nm，转矩脉动保持在士0.5 Nm范围以内，PI控制时，转矩脉动在士 0.9左右，滑模变结构控制时，转矩脉动在0.7左右。可见在抑制转矩脉动方面，自抗扰控制比其他两种控制方式效果更明显。

为了验证ADRC控制方式下SR电机的转速响应情况，给定转速500r/min，进行了转速响应测试实验，在空载运行与带负载运行情况下转速实测波形如图11所示。从图11可看出，两种情况下，SR电机转速都能快速响应，动态调节过程短，很快达到给定转速进入稳态运行。

图11 ADRC控制转速响应曲线

4 结 论

自抗扰控制通过实时估计出SR电机所受的总扰动，并及时予以前馈补偿，增强了SR电机对各种扰动的鲁棒性，有效地抑制了转矩脉动，仿真结果验证了控制策略的正确性与有效性。