侧围裙边梁烘烤变形原因分析及防止再发方案

高满银

（北京汽车股份有限公司 生技中心，北京 101300）

0 引 言

白车身由焊装车间进入涂装车间进行面漆喷涂，涂装工艺顺序为：电泳前处理、阴极电泳、电泳后处理、面漆喷涂等。电泳后处理工序包括流动冷水冲洗和高温烘干2个过程。某车型侧围外板材质为DX56D+Z，板料厚度为0.7 mm。在样车试制阶段，白车身进入涂装车间进行电泳后处理的烘烤过程中出现侧围裙边发生凹坑变形的问题，如图1 所示，发生频率在95%以上。通过各种渠道了解，虽然此类问题在汽车制造业内并不常见，但也并非偶然发生，存在一定的发生比率，只是变形的严重程度稍有区别。在解决此问题的过程中，从冲压工艺、车身工艺、涂装工艺3个环节逐一进行排查和验证，发现此问题发生的原因复杂，且难以进行定量分析。

1 冲压残余应力分析

图1 侧围裙边烘烤变形问题

冲压拉深成形过程是先发生弹性变形，再发生塑性变形。由于汽车外覆盖件形状复杂，在拉深成形过程中各部位发生的塑性变形不均匀，当拉深载荷消失时，冲压件要恢复弹性变形，会发生回弹现象，当释放拉深载荷时，仍有部分应力残留，当没有外部因素作用时，此部分应力可在冲压件内部保持平衡，为残余应力[1]，但不会造成零件变形。由于零件形状的原因，不同的部位强度不同，造成不同部位的弹性变形恢复程度不一样。弹性变形恢复程度高的部位，产生的回弹应力小，弹性变形恢复的程度低，产生的回弹应力大。实践证明，回弹应力能使冲压件产生变形，只是变形程度会随应力大小及零件的强度有所不同。

利用CAE 分析软件AutoForm 对此侧围裙边回弹后的应力进行分析，如图2 所示，回弹残余应力在-12.3～6.4 MPa，此应力大小不足以使侧围裙边产生能观测到的变形，且冲压件实物也不存在变形。理论上，此应力在冲压件焊接后会恢复到回弹前的状态，有利于提升冲压件的强度，能提高零件抗变形的能力。

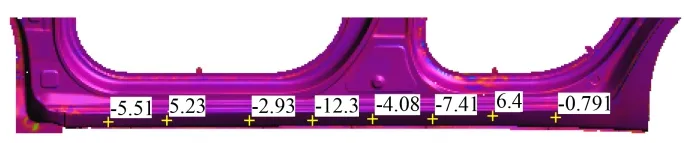
图2 冲压回弹残余应力分析结果

2 焊接应力分析

焊接过程中，由于零件精度误差及焊接工装夹具制作精度误差的存在，焊接后，钣金件会脱离理论状态发生微量弹性变形，严重的会发生塑性变形。此案例中，焊接后并未发现可观测到的变形。有变形就会产生应变，发生应变会随之产生应力，即焊接应力[2]。

通过零件的实测精度数据即白车身三坐标监测数据建立数学模型，用AutoForm 模拟考虑实际精度误差的焊接工况，对其焊接应力进行分析，结果显示发生变形位置的焊接应力为-1.55～3.29 MPa，如图3 所示，此应力不足以使侧围裙边产生能观测到的变形，且白车身焊接完也未产生裙边变形的问题。此应力有可能对白车身进入涂装车间电泳后烘烤过程中裙边产生变形有一定的影响，但具体比率还需要与后续分析结果进行比较。

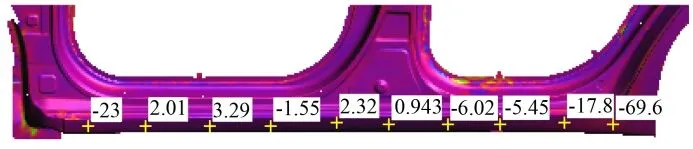
图3 焊接应力模拟分析结果

3 烘烤受热膨胀应力分析

白车身电泳完成后，进入烘烤工位，由车身两侧的烘烤炉向车身喷洒经过加热的空气，最高温度为200 ℃。由于白车身是由许多钣金件焊接而成，车身内部存在大小不同的腔体，导致在整个车身升温的过程中，内外钣金件的升温速度不一致，导致在同一时刻，内外钣金件产生温差。为了获得温差数据，在发生变形部位腔体内外设置了温度传感器，通过传感器采集温度数据形成了不同部位的升温曲线，通过比较发现在侧围下裙边位置，内外钣件的最大温差达到58 ℃，如图4所示。

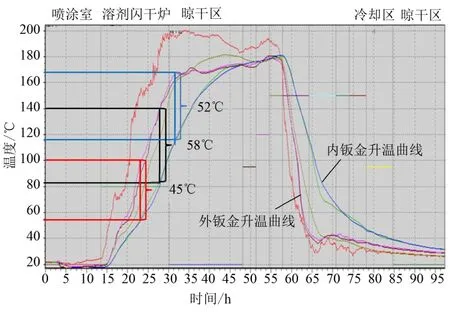
图4 烘烤升温曲线

由于内外钣金材质均为冷轧钢板，虽然牌号有所不同，但主要成分区别不大，内外钣金件具有相同的膨胀系数，该温差会导致内外钣金在同一时刻的热膨胀量不一致。经过测量，侧围裙边的长度为2 014 mm，如图5中所示的常温状态。

根据升温曲线，在外钣金处于150 ℃的时刻，内钣金温度为92 ℃，假定内外钣金相互独立、互不制约，根据热膨胀量计算公式ΔL=ΔT×α×L，其中膨胀系数α=12.8×10-6，内外钣金的膨胀量分别为约3 mm和1.5 mm，如图5所示的独立升温状态，此刻内外钣金热膨胀差为1.5 mm。由于内外钣金焊接在一起，且内钣金强度远高于外钣金强度，如图5 所示的焊接升温状态，内外钣金热膨胀量差导致外钣金受到来自内钣金的1.5 mm压缩应变。

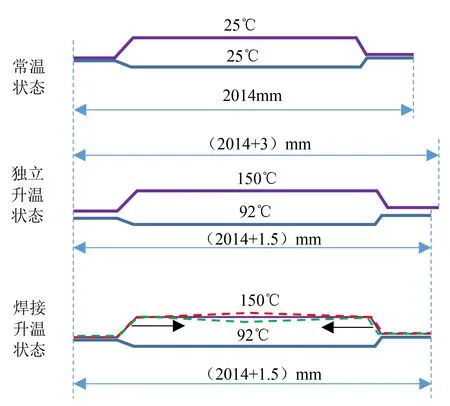
图5 内外钣金温差及热膨胀量差示意图

根据应力应变计算公式ε=ΔL/L，σ=Eε=E×ΔL/L（弹 性 模 量E=220 000 N/mm²）计 算：ε=ΔL/L=1.5/2 014= 0.000 74，σ=Eε=220 000×0.000 74=164 MPa，外钣金件此刻受到的压应力约为164 MPa。

根据某钢企选取5 个0.7 mm 厚的CX56D+Z 材料试样进行试验的平均数据显示，随着温度的升高，金属的屈服强度会降低，如图6所示。结合外钣金随着温度受到的压应力曲线可以看出，在烘烤过程中，当外钣金温度超过100 ℃时，外钣金所承受的压应力已超出其在此温度时的屈服强度，从这点可以解释为什么烘烤之后侧围裙边产生了变形。

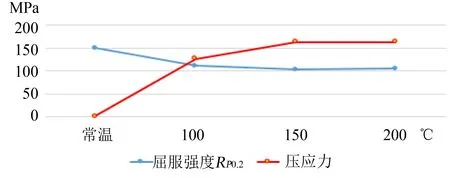
图6 CX56D+Z材料屈服强度和外钣金所承受的压应力与温度的关系

但此时的外钣金已拉深成形，经过塑性变形后，由于加工硬化的原因，常温下侧围零件的屈服强度已不同于原材料的初始屈服强度，侧围零件的屈服强度会高于原材料的初始屈服强度。

加工硬化是指在冷变形时，随着变形程度的增加，金属材料的所有轻度指标和硬度指标都有所提高，弹塑性和韧性有所下降[3]。经过CAE 分析及实际测量，侧围拉深的应变为0.015，根据硬化曲线公式：

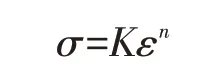
其中，硬化系数K=519.7，硬化指数n=0.222，σ=Kεn=519.7×0.0150.222=205 MPa，经过计算，此时在常温下侧围外板裙边位置加工硬化后的屈服强度提升到290 MPa，根据原材料的屈服强度随温度升高而降低的规律推算，150 ℃时加工硬化后的屈服强度降低到150 MPa 左右，但仍小于此时侧围裙边承受的压应力164 MPa，如图7 所示，理论上会产生压缩塑性变形。

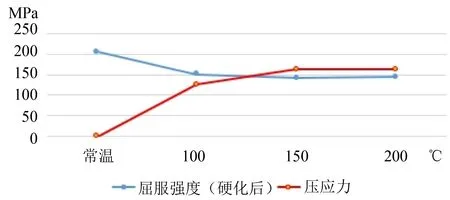
图7 侧围裙边硬化后屈服强度和外钣金所承受的压应力与温度的关系

侧围采用厚度分别为0.7、0.8 mm 的板料，根据应力应变的计算公式，外钣金承受的压应力和屈服强度相同，所以烘烤时2 种厚度的侧围发生的变形程度应该一样。但经过实践验证，更换为0.8 mm 厚的同材质板料，变形发生率为0，其结果完全不同于采用0.7 mm 厚的板料的结果，实践验证结果与上述理论分析结果不相符。

上述提到的应力应变理论的前提是承受压应力的物体只发生受力方向的压缩变形，没有发生垂直于受力方向的弯曲变形，解释的是上述前提下样件在受到压应力的时候，压应力与压应变的关系。如果压应力超出屈服强度，会发生压缩塑性应变[4]，如图8所示。

白车身进入涂装车间电泳后烘烤时侧围裙边产生凹坑变形的破坏形式是垂直于受力方向的变形，不同于压缩应变的形式。

4 压杆失稳理论

压杆失稳是指细长杆在受到轴向压力作用下，当压力超出细长杆所能承受临界载荷时，不只产生轴向压缩变形，还在横向产生弯曲变形，导致破坏。失稳一是与所承受的压力大小有关；二是与压杆的长度有关；三是与压杆截面几何形状（惯性矩）有关；四是与杆件的材料力学性质（弹性模量）有关[5]。压杆失稳理论如图9所示。

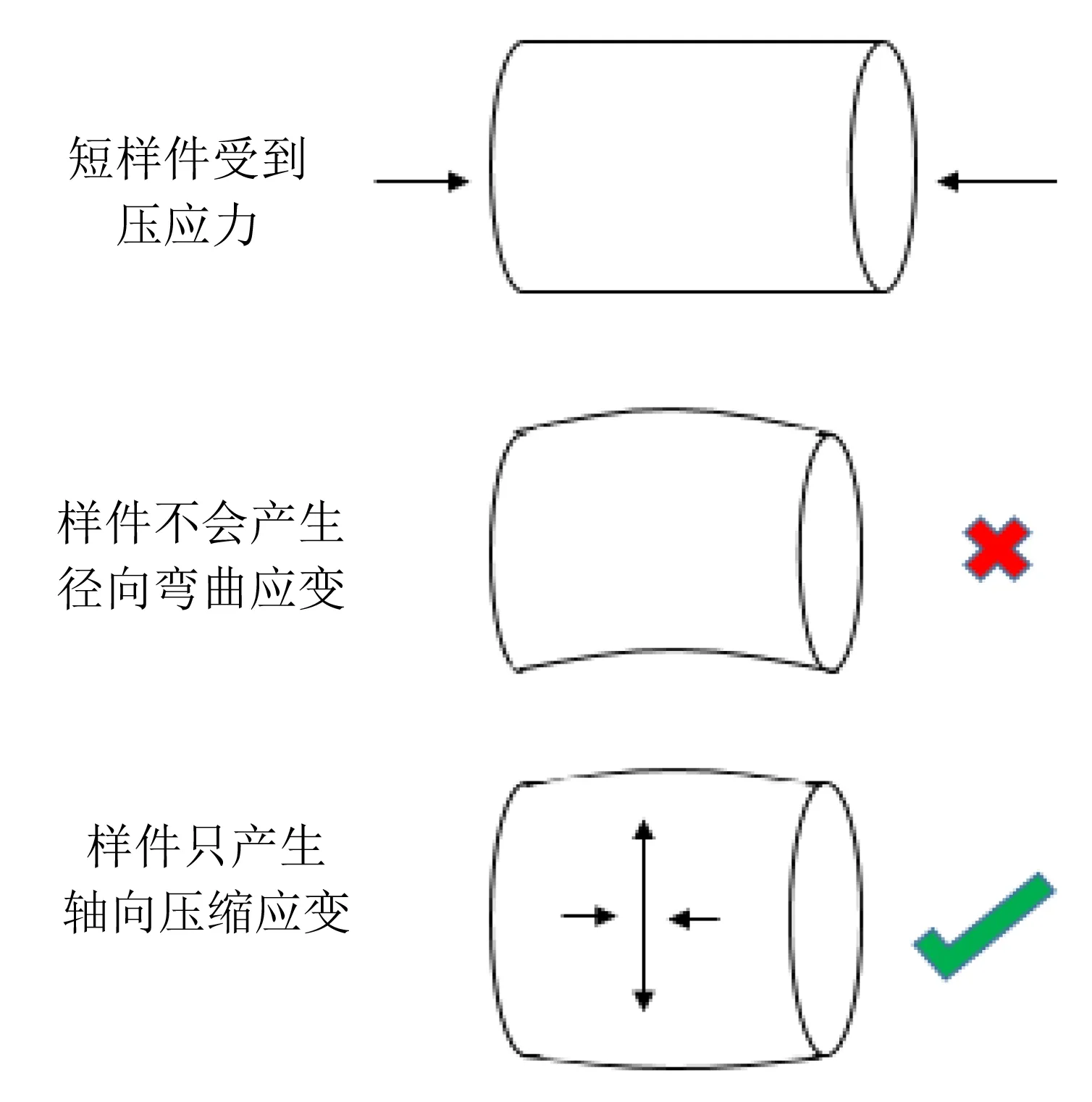
图8 压应力应变

临界载荷计算公式为：

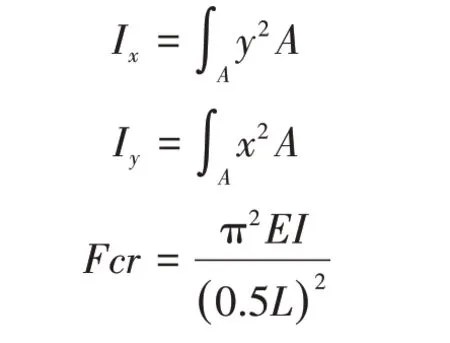
其中，E 表示钢材弹性模量；I 表示零件的最小惯性矩，N·m；L 表示零件的长度，mm；Fp 表示所承受的压力，MPa；Fcr 表示细长杆的失稳临界载荷，MPa。

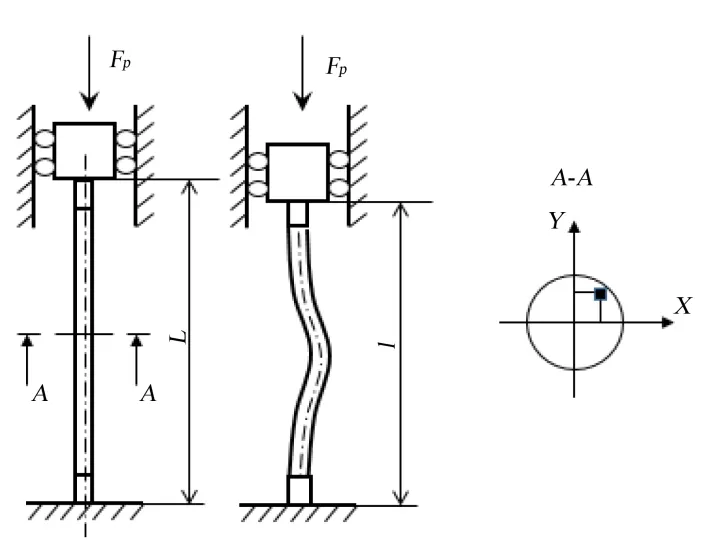
图9 压杆失稳理论示意图

杆件的失稳临界载荷反映了零件的抗失稳变形的能力，临界载荷越大，零件的抗失稳变形能力越强。从临界载荷的计算公式看，当零件的长度及材质（材质决定弹性模量E）确定后，决定零件抗失稳变形能力的关键因素就是零件横截面的几何形状，即横截面的惯性矩I。

规则截面的惯性矩可通过查询标准公式进行计算，但非规则截面的惯性矩难以用公式进行计算，可通过绘图软件AutoCAD 里的MASSPROP 命令计算非规则截面的惯性矩。

5 烘烤变形根本原因分析

侧围裙边平缓的特征曲面宽度约为50 mm，烘烤后变形的位置也位于此平缓的特征曲面上，因此截取悬长为50 mm 的曲面进行分析，并截取5 个位置的截面分别计算0.7、0.8 mm 厚板料的惯性矩，位置选取如图10所示，计算结果如表1所示。

通过计算结果发现厚度为0.7 mm 的侧围在位置②和位置③的惯性矩最小，而这2 个位置正是实际烘烤变形最严重的位置。厚度为0.8 mm 的侧围相应位置的惯性矩比0.7 mm 的侧围高出约13%，说明0.8 mm 的侧围比0.7 mm 侧围的抗失稳变形能力提升了13%。

经过验证，更换为0.8 mm 厚的板料后，解决了烘烤变形的问题，验证结果符合理论分析的结果，说明是因为侧围裙边的截面惯性小导致其抗变形能力低，而烘烤时内外钣金的温差导致外钣金受到的压应力超出其失稳临界载荷应力，因此发生了凹坑变形。

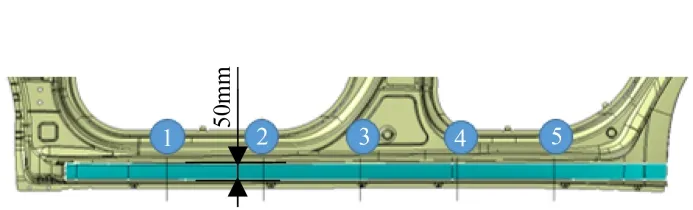
图10 发生烘烤变形的侧围裙边位置悬长50 mm截面

表1 侧围裙边不同位置的最小惯性矩

为了验证该分析结果，对此侧围裙边进行了校核，目前还没有相应的CAE 软件可以进行全方位的辅助模拟计算，只能基于假设的理想条件进行手工核算。本案例中侧围裙边实际变形区域大约50 mm×50 mm，因此在此位置截取了长度为50 mm ×（80～100）mm 的片段进行独立校核分析，如图11所示。

理想条件下将截取的片段长度和最小惯性矩值代入临界载荷计算公式计算该片段的抗失稳临界载荷。

临界 载 荷压力：Fcr=（π²EI）/（0.5L）²=（3 010～4 704）N，位置②和位置③悬长为50 mm的截面积约为32.5 mm²，可计算其抗失稳临界压应力为：临界载荷 压 应 力Rq=Fcr/S=（3 010～4 704）/32.5=92～144 MPa。

根据不同温度点侧围外钣金所承受的压应力（见图7），发现在侧围外钣金温度达到150 ℃时，所承受的压应力为163 MPa，已超出位置②和位置③的临界载荷压应力上限144 MPa，如图12所示，因此在位置②和位置③发生了失稳变形。

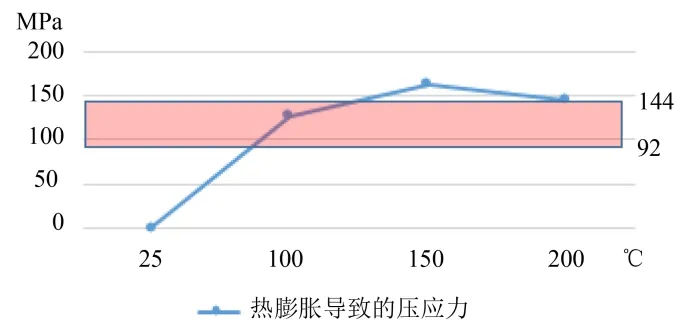
图12 侧围外板承受的压应力与临界载荷压应力的对比

从理论分析到理论校核再到实践验证，可以得出以下结论：烘烤过程内外钣金升温速度不一致导致同一时刻内外钣金热膨胀量不一样，导致外钣金承受的来自内钣金施加的压应力超出零件的抗失稳能力的临界载荷，最终导致侧围外板在截面惯性矩相对较小的位置产生永久的破坏性变形，这是导致发生此问题的根本原因[6]。

6 防止再发生对策

从分析过程来看，虽然可以断定烘烤时内外钣金的升温速度不一致，导致的外钣金承受的压应力超出侧围裙边的抗失稳能力是导致此问题发生的根本原因，但并不是唯一的原因，温度升高导致钣金强度降低也产生了一定的影响。通过增加侧围外板板料厚度（由0.7 mm 改为0.8 mm）提升了截面最小惯性矩，从而提高侧围钣金抗失稳变形能力的办法解决了烘烤裙边变形的问题。但以上理论分析是基于截取片段在假设理想条件下进行的独立分析，实际上选取分析的片段并非对立存在，其边界与周围钣金是有耦合作用的，且焊接应力也会对实际结果产生一定的影响，所以此问题的发生是各种原因综合作用的结果。因此在假设理想条件下的分析结果虽然反应了问题的根本原因，可为问题定性，但还需更多的试验数据支撑为其定量。

为了得到更可靠的数据支撑，对8 款车型进行了对标分析，如表2 所示，从对标分析统计结果看，侧围裙边悬长为50 mm 的截面最小惯性矩设计值I＞3.5 比较安全，8 个对标样本里截面最小惯性矩设计值I＞3.5 的车型均未发生变形。但仔细观察会发现第3个侧围相应惯性矩I=3.3＜3.5，实际上并没有发生类似的变形问题，说明实际情况比理论分析要复杂，此处只是对局部强度进行了分析，分析维度过于单一，不能覆盖所有情况，不足以说明全部问题。

为了更全面地反应真实情况，增加了分析维度，增加下半段截面及全截面的最小惯性矩对标分析。由于后4 个车型的50 mm 悬长惯性矩远大于前4 个车型，且没有发生变形的问题，只对前4 个车型增加了分析维度的对标分析，如表3 所示。从对标分析结果看，第3 个车型的悬长50 mm 截面最小惯性矩虽然小于其他车型，但下半部分截面惯性矩和整体截面惯性矩远大于其他车型，也就是说其整体的抗失稳变形能力远大于其他车型，这是该车型没有发生烘烤变形的主要原因。

根据以上理论及对标数据分析，可初步确定侧围裙边截面最小惯性矩的设计标准，因对标数据有限，可适当加大安全量，如图13所示。

7 结束语

在汽车车身制造过程中，冲压回弹残余应力、焊接应力及烘烤热膨胀产生的应力无法避免，当应力超出零件抵抗变形的能力时，就会发生破坏性的变形[7]。解决此类问题最有效的办法是提高零件的抗变形能力，在产品设计阶段，充分考虑零件的抗变形能力。而最能反映零件设计抗变形能力的指标就是零件截面的惯性矩，提高截面惯性矩的办法有2 种：增加截面面积和改变截面的形状。增加截面面积就是增加冲压件的厚度，会导致成本增加，因此建议在不影响零件功能设计的前提下采用优化产品截面形状的方法来提升截面惯性矩，以此提升零件的抗变形能力。

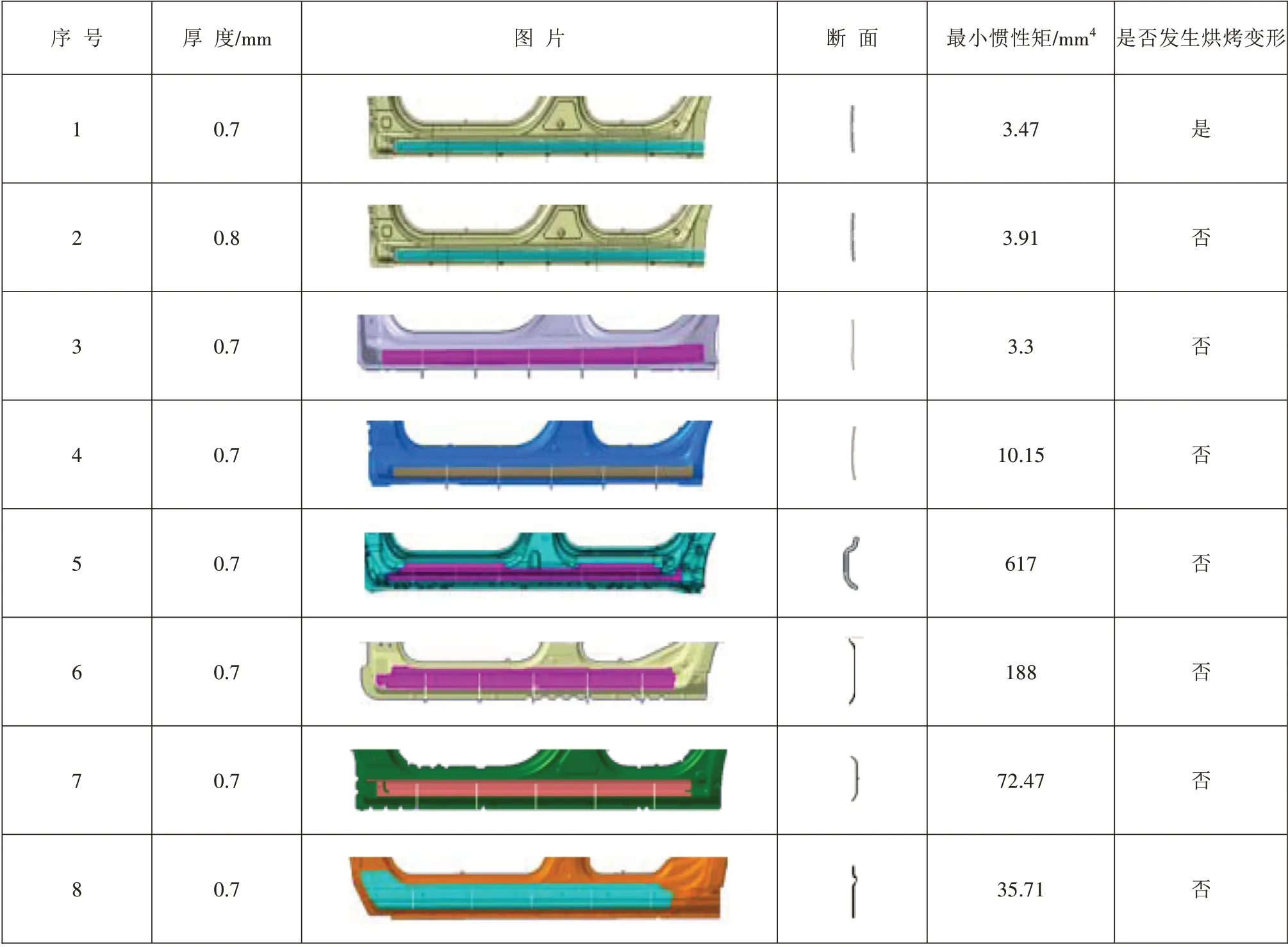
表2 不同车型侧围裙边悬长50 mm截面惯性矩对标

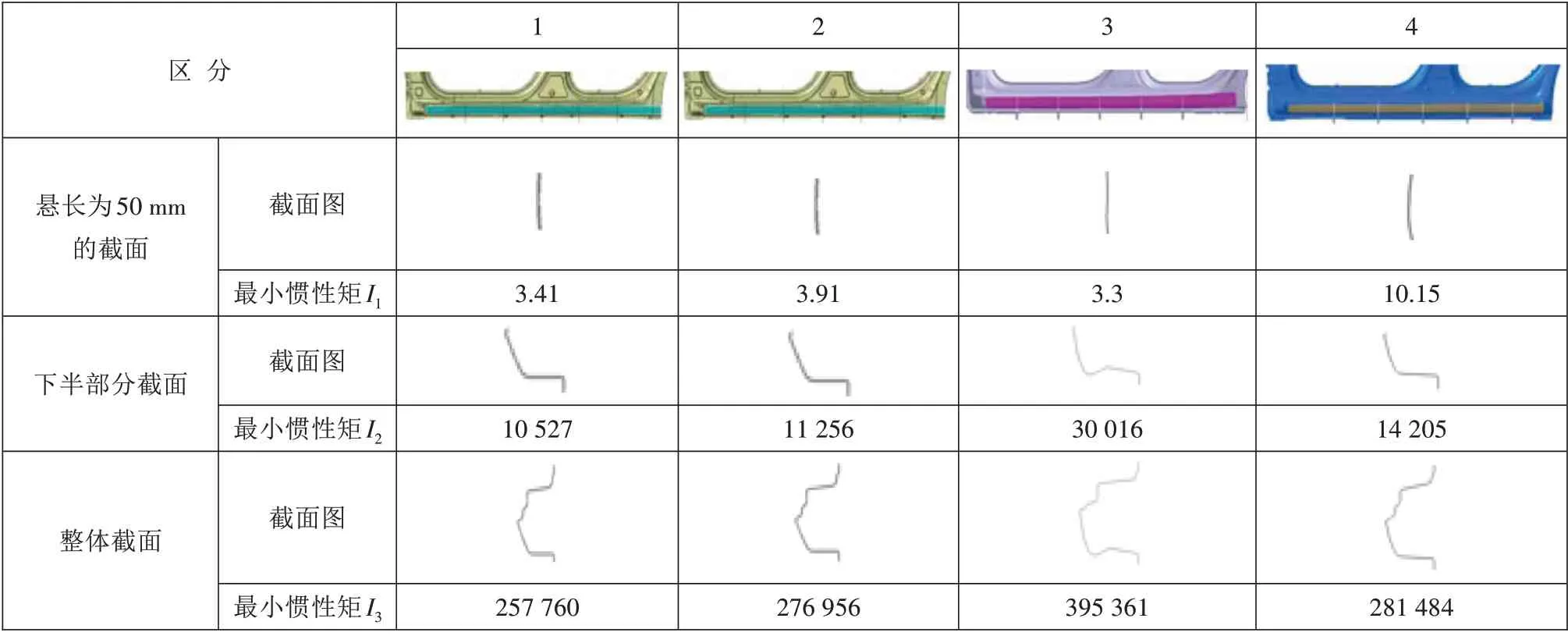
表3 3种截面最小惯性矩对标分析

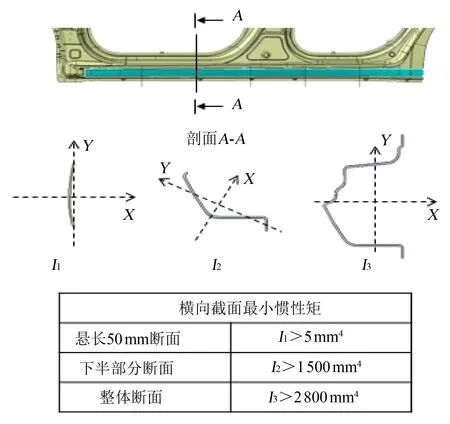
图13 侧围裙边截面最小惯性矩设计标准