中低压配电网接地故障识别模型设计 ①

李鹏飞

(延安大学物理与电子信息学院，陕西 延安 716000)

0 引 言

进入二十一世纪以来，我国在电力行业取得了日新月异的发展，配电网建设工程日渐完备，为居民与企业等均提供了高质量的电力服务，满足其不同的用电需求[1]。然而随着用电需求的不断攀升，配电网在电力系统中的重要性也愈加凸显，其对故障的识别能力与运行的可靠性，与能否进行正常稳定的供电工作息息相关。传统的配电网建设手段与其故障识别模型，已然不能满足当前的供电需求[2]。有鉴于此，此次研究将中低压配电网中的接地故障作为探究的重点对象，应用小波变换的方式来构建相应的故障识别模型，以期能够解决电力发展中的核心问题，保障故障识别的高效性与精确性。

1 小波变换在配电网接地故障识别中的模型构建

1.1 小波变换算法研究及优化处理

小波变换是一种能够有效提取出信号局部化特征的方法，具有较强的分析提取能力，在时域与频域中分别分解原始信号，得到细节分量，且该细节分量具有不同的分辨率，以显著突出原始信号的局部化特征[3]。小波变换的应用范围极其广泛，这归功于其时频窗口的灵活性，小波变换的基本公式如式(1)所示。

(1)

对式(1)进行频率域的变换，令平方可积函数ψ(t)∈L2(R)，当其满足傅立叶变换时，则有式(2)。

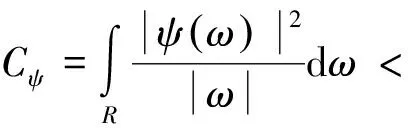
(2)

根据式(2)可知ψ(t)为小波母函数，对其再次进行相应的平移变换与伸缩变换，即可获取到一组函数，其定义公式见式(3)。

(3)

在式(3)中，a代表着进行伸缩变换时的尺度伸缩因子，而进行平移变换时所需的位置平移因子则以τ来表示。针对在空间中的任何一个函数f(t)，若该函数满足f(t)∈L2(R)，即可选择恰当的小波母函数并对其进行展开处理，则可得到连续小波变换的表达式，如式(4)所示。

(4)

同理可知，可以根据连续小波变换进行再重构处理，进而得到变换前原始信号的函数f(t)，在小波变换的过程中，存在部分多余的信息，故而应对τ应用均匀离散的手段，对a则进行幂级数离散化处理，该种处理过程被称为离散小波变换[4]。当位置平移因子τ的取值设置为1，且a0=2时，离散小波变换可进一步转换为二进小波变换，其转换形式见式(5)。

(5)

在式(5)中，尺度因子a发生了变化，需要将对应尺度的轴进行频率划分，以实现对整个频率轴的完全覆盖。位于时间轴中的平移因子可表示为b，且b满足二进制的取值要求，存在b=n/2m。小波变换的时频窗口如图1所示。

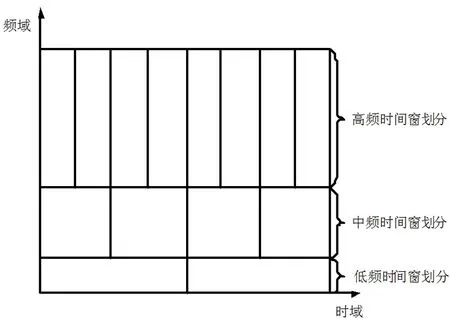
图1 小波变换过程中的时频窗口

根据图1可知，小波变换具有一个极其显著的优势，当其位于不同的频率环境下时，其时域中的窗口长度具有可调节性，可依据变换的各种需求来改变长度。在配电网故障识别与分析过程中，信号的频率与窗口的宽度呈负相关关系，该频率与窗口的高度却呈正相关。

1.2 基于优化后小波变换的配电网故障快速识别

配电网故障指的是在对电力资源进行分配时，相与相(地)之间的不正常连接情况[5]。配电网故障通常按照接地或连接方式的不同来进行分类，包括单相接地故障、两相短路故障、两相接地短路故障，以及三项短路故障共四种类型；单相接地故障一种最为常见的配电网故障类型，且危害性较大，往往表现为配电网中绝性能较弱的地方被击穿等，若在该种故障发生后不及时停止系统的运行，则会发生故障扩散；两相短路故障，其发生的概率小于前者，但其严重性更强，因为会产生巨大的故障电流，对系统造成更大的危害。两相接地短路故障蕴含零序电流；三相短路故障发生概率最小，严重性最强，且是四种故障类型中唯一的对称性故障。在配电网中，所有线路通常均由A、B、C三相构成，发生单相接地故障时的电流分布如图3所示。

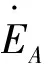
(6)

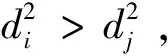
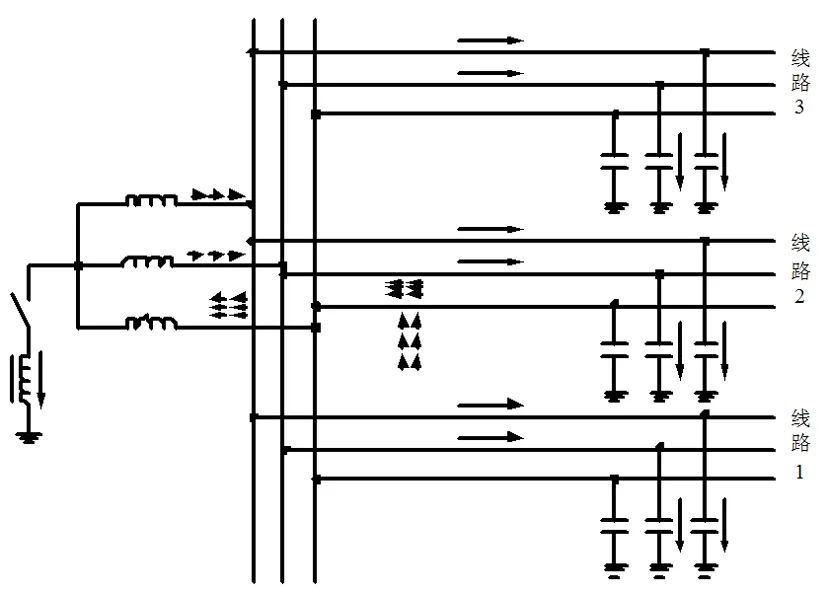
图2 A相发生单相接地故障时的电流分布示意图

2 小波变换在中低压配电网故障识别的仿真分析

以小波变换为核心技术，将其应用到对配电网中性点电压的分解与重构处理当中，可以准确判断出接地故障出现的时间；随后对暂态零序电流进行处理，获取接地相线路；最终对所有信息进行整合处理，即可实现配电网故障类型的准确识别。对中性点经消弧线圈接地系统进行仿真分析，如图4所示。

图3中的仿真参数需要预先进行设置，以确保仿真分析的准确度。其中包括仿真分析的初始时间、相对容差、绝对容差，以及步长等。在配电网接地系统中，各个出现的首部均具有相应的三相电流与电压的测量模块，其输出值为零序电流与零序电压的三倍。当故障相电压为最大值时，该电压的波形及其分解重构图见下。

图3 中性点经消弧线圈接地系统仿真模型

图4 最大故障相电压值的波形及其分解重构图

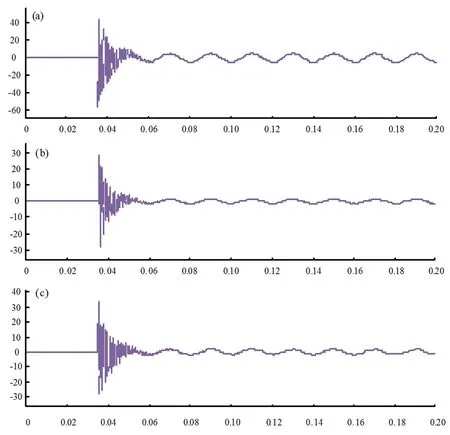
图5 最大故障相电压值的三条不同线路零序电流波形图

图4(a)为故障相电压为最大值时的中性点电压波形图，图5(b)则展现出该状态下的小波分解重构图。根据图4可对中性点的电压波形有一个较为清晰的认识，可知该配电网系统中故障发生的时间点为0.035s，而对故障点所在波形峰值处的横坐标进行放大处理后，得到的值为0.0351s。将获取到的两项数据进行对比可知，利用小波变换得到的故障时刻值误差极小，仅为万分之一秒。在相同的仿真条件与环境下，对各个线路的零序电流进行仿真分析，其结果如图5所示。

图5中的三个小图(a)、(b)、(c)，分别表示着配电网中三条不同线路的零序电流波形，对其进行对比分析可知，上述三条线路中的零序电流波形走势基本保持一致，但具体的数值略有不同。为了得到更为精确的结果，研究中对此零序电流波形进行相应的分解处理，采用一维离散四尺度来进行该操作，进而获取分解结果；随后再对该其中的高频细节进行小波重构处理，得到如图6所示的重构波形结果。

图6 最大故障相电压值的三条不同线路零序电流分解重构图

通过对图6进行分析可知，当处于相同的时间点时，线路L2与线路L3的零序电流重构波形走势基本保持一致，显示出其极性的同一性。而线路L1则与上述二者不同，其中突变量的峰值显著高于二者，且极性不一致，方向相反。综上所述，可以准确地对故障点位置进行判断，即L1为该配电网中的故障线路。当故障相电压值为0时，中性点电压波形及其小波重构图见图8所示。

图7 故障相电压值为0时的波形及其分解重构图

图7(a)呈现出故障相电压取值为0时的中性点电压波形图，图7(b)则展现出该状态下的小波分解重构图。配电网系统中的故障发生于0.06s之时，对该横坐标同样进行放大处理，可获取到与该波形峰值相匹配的横坐标值为0.061s，二者之间差值为千分之一秒，误差仍小至可忽略不计。故而表明利用小波变换来对配电网线路进行故障识别，其识别精度较高，效果较优。

3 结 论

当前社会经济水平不断提升，城市现代化进程也不断加快，与此同时，人们各方面的用电需求持续增大。在电力系统运行的过程中，配电网起着不言而喻的重要作用，配电网的稳定运行直接影响着人们的正常用电与安全用电。为了使配电网中的故障无所遁形，使其供电可靠性有所保障，此次研究应用小波变换来构建配电网故障识别模型，并详尽分析了配电网常见的故障类型与表现形式。结果表明，当故障相电压值取最大值时，故障发生的时间点为0.035s，而利用小波变换得到的故障时刻值误差极小，仅为0.0001s。尽管本次研究有幸取得了一定的成果，发现小波变换在配电网故障识别中的可靠性与高性能，但仍然存在部分不足之处，如进行的仿真分析不够全面等，望在未来的研究中能够多加改进。