明挖地铁车站对邻近管线安全性分析及控制措施研究 ①

王余鹏， 韩 伟

(福建林业职业技术学院,福建 南平 353000)

0 引 言

随着都市延伸，地铁建设成为解决道路堵塞的一剂良药，在复杂多变的地质状况下，需要保证地铁明挖施工及邻近构造物的稳定。本文以目标管线沉降的实地监测值为基础，结合整体数值分析法对比评价，研究地铁明挖施工对邻近管线安全状况作评价是有重要含义的。

1 工程概况

排下车站位于螺州路以北的福峡路下方，沿福峡路西北～东南向布置。主体为地下两层岛式月台车站，长为262.608m，宽为17.8m，采用明挖顺筑法施工[1]。周边遍布居民住宅，沿线燃气、雨水、污水、电力、军用电缆等地下管道线路众多，且工程地质条件复杂，土质软硬不均、地下水丰富，对地铁明挖的稳定性控制非常重要。

2 基坑安全等级及围护设计方案

2.1 工程地质概况

根据地质勘察资料，基坑底面南侧为残坡积层及风化岩层[2]，地层变化较大，个别部位存在强度较高的孤石，土层物理力学性质指标见表1。

(1)潜水

孔隙潜水主要赋存于①填土中[3]。潜水的埋深深度为0.70～1.50m，水位标高约为3.52～4.33m。

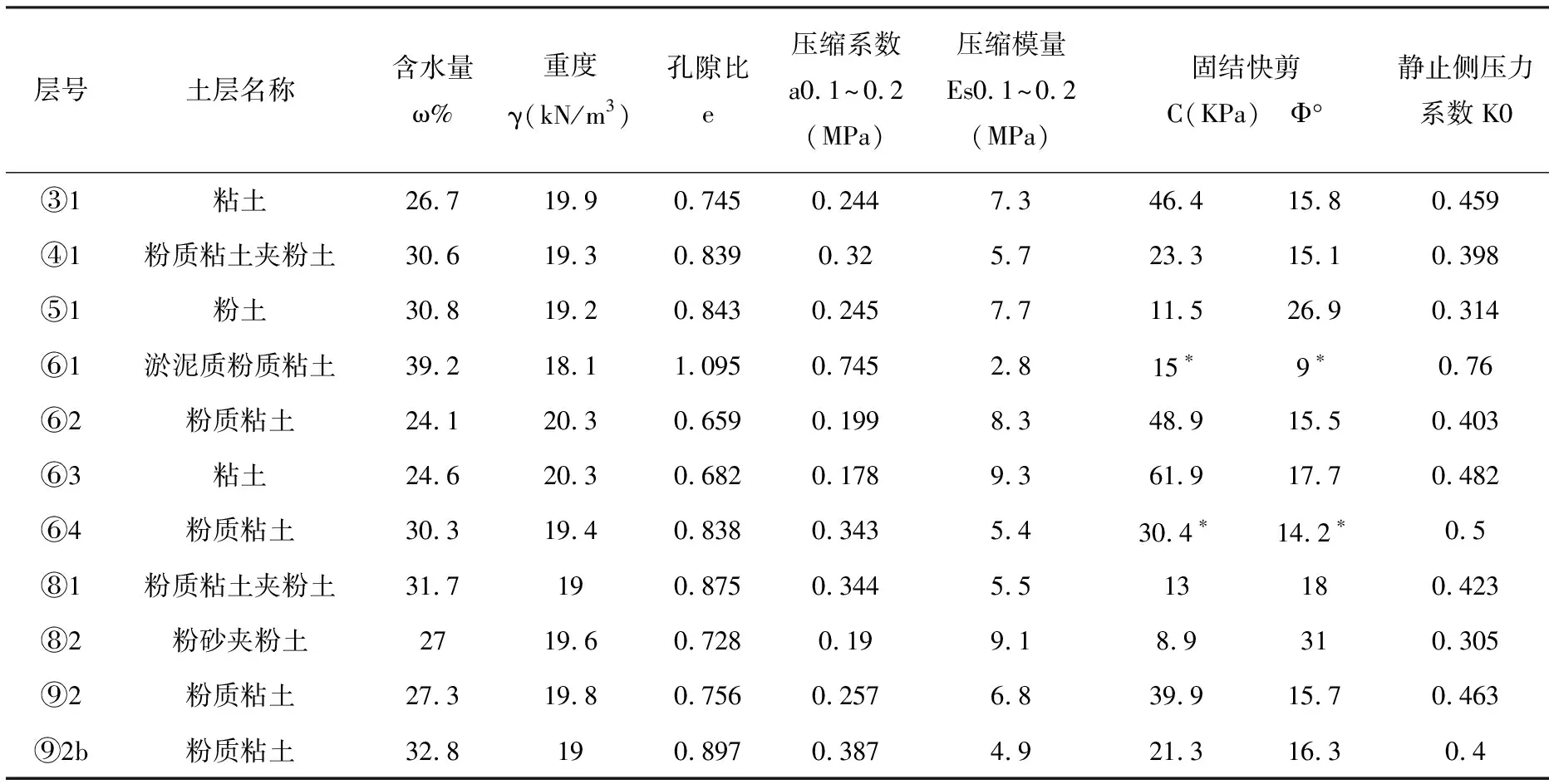
表1 土层物理力学性质指标

图1 排下站地理位置

(2)承压水

承压水分为第Ⅰ层承压水和第Ⅱ层承压水。第Ⅰ层承压水埋深为地面下2.82～3.32m，标高为1.71～2.10m，第Ⅱ层承压水埋深为地面下 9.69～9.73m，标高为-4.64～-4.72m。

2.2 基坑安全等级及环境保护标准

车站周边两侧地下管线密集，主要管线为雨水、煤气、污水等市政管路，管底埋深约在2.8-4.3m左右。管线情况较为复杂，施工时要注意各管线的情况，避免发生管辖的破坏，采用探地雷达对车站四周及地面进行管线位置探测(图2)。

图2 明挖范围内管线探测图

(1)污水管(砼、DN700、埋深2.45m)，位于明挖西侧，距离明挖施工区域距离11.8m。

(2)煤气管(铸铁、DN600、埋深1.67m)，位于基坑西侧，距离基坑边距离9.7m。

(3)雨水管(砼、DN700、埋深3.1m)，位于基坑东侧，距离基坑边距离6.7m。

综合车站明挖施工环境，将距离明挖坑边缘最近的雨水管道安全保护等级定为二级，即坑外地表最大沉降量≤0.2%H，H为基坑深度。

2.3 基坑围护设计方案

本站主体围护横剖面图如图3：

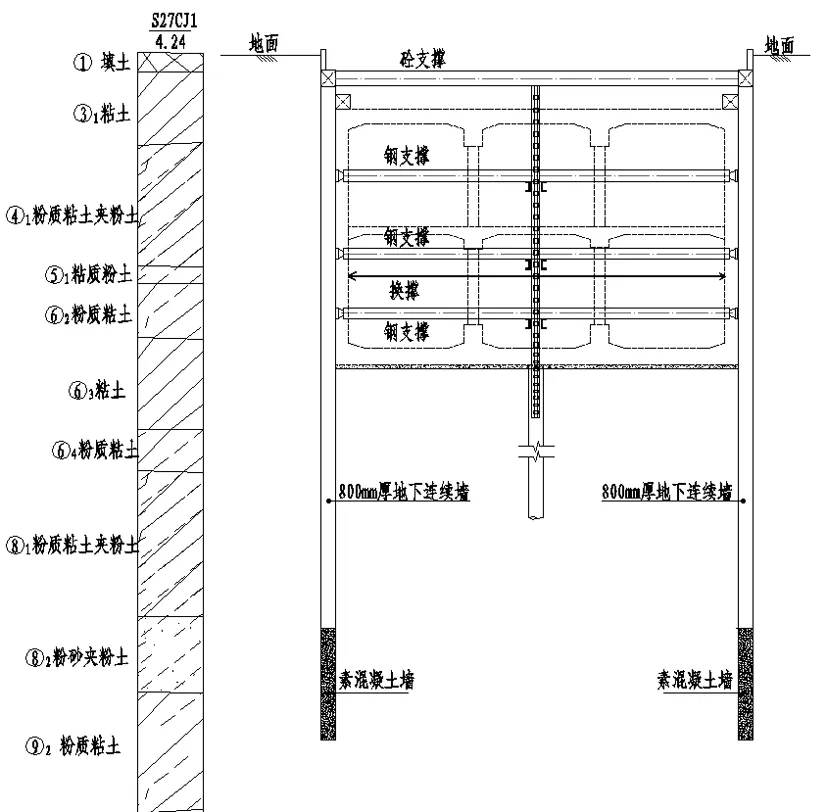
图3 标准段围护结构横剖面图

明挖施工纵深约17.3m，从围护结构横剖图可知，车站坑底基本位于⑥3层粘土层。标准段土层物理力学性质指标见表2：

明挖基坑标准段的第一道混凝土支撑截面为800mm×800mm，水平距离为7m～9m，顶圈梁截面尺寸为900mm×800mm，系杆截面尺寸为400mm×600mm[4]，其余钢管支撑为Φ609×16，间距3m左右。支撑下采用4L140×14型钢格构柱加Φ800钻孔灌注桩作立柱桩，立柱截面尺寸为420mm×420mm。

施工顺序：

(1)沿车站向下施工至第一道混凝土支撑位置[5]，进行冠梁及挡土墙施作(第一道支撑以下500mm)；

(2)架构第一道支撑后，继续明挖施工至钢架构位置(第二道支撑以下500mm)；

(3)开挖至基底，并施作垫层、防水层[6]、底板、结构柱，拆卸降水井，设置泄水孔；

(4)将第三道支撑向下移作为换撑支在侧墙上，继续同时向上施工侧墙防水层，侧墙和柱，浇筑中板；

(5)需等到中板混凝土强度满足规定值，拆卸钢架构支撑，同时施工侧墙防水层[7]，浇筑顶板；

(6)待顶板混凝土强度满足规定值，拆卸顶端混凝土架构，并施工顶板防水层，及时恢复道路通车。

表2 土层物理力学性质指标

3 分析方法

由于车站明挖施工会引起的土层运动，造成邻近管线的附加受力和变形。如果变形过大，则会使管线破裂或损坏，引起安全事故。基坑开挖影响方法：(1)两阶段分析法；(2)整体数值分析法。整体数值方法是从整体上分析车站明挖与邻近管道施工过程的彼此影响。它借助大型的商业有限元软件来分析基坑开挖各个阶段相邻管道的情况，并采用整体数值方法进行分析和计算，可以合理模拟基坑明挖的复杂施工过程[8]。

3.1 两阶段分析方法

基于Winkler弹性地基梁模型的两阶段位移法，是把基坑周边的管线模拟为弹性地基梁，将车站明挖施工的岩体位移作为边界前提施加于地基梁上，得到管线和岩体的相互作用的位移方程，采用有限差分法对管线的附加变形和受力分析。

(1)建立弹性地基梁隔离体平衡方程

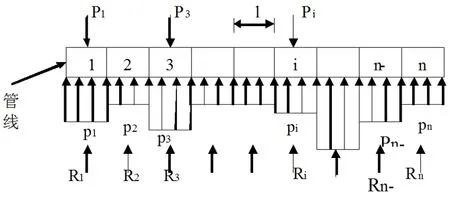
图4 管线受力示意图

如图4所示，将管线视作弹性地基梁，均分为n个单元，单元长度l，管线总长L=nl。作用在单元i的均布外力Pi，地基反力合力Ri

弹性地基梁的微分方程为：

(1)

不考虑管线与土体的滑移，则弹性地基梁的位移w与土体位移s相等，即w=s，则：

(2)

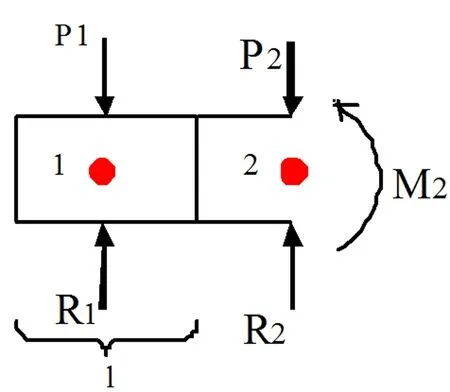
图5 管线取隔离体示意图

如图5，将地基梁在节点2处切开，节点2处弯矩M2

M2=R1l+M2p

(3)

I2为单元2的截面惯性矩；E2为单元2的弹性模量；M2p为节点2左侧外荷载对该点的力矩，另顺时针为正则M2p=-P1l。

联立式(2)和式(3)，表示为差分形式：

(4)

依次从节点2至节点(n-1)将单元切开，求得各断面处的弯矩，将微分方程表示为差分形式，获得以下(n-2)个平衡方程：

(5)

其中

(6)

将上述(n-2)个方程写成矩阵形式为：

(7)

(2)边界条件——静力平衡条件

因弹性地基梁纵向尺寸较大，近似认为距离基坑较远处的管线不受约束，为自由边界条件，端点处的弯矩与剪力均为0。对整个弹性地基梁建立静力平衡得到：

(8)

其中

(9)

联系式(8)、式(9)将地基反力Ri=kilDsi代入，得到n×n阶矩阵方程(10)。已知管线的外力{P}，由方程(10)便可得到弹性地基梁的位移{s}。

(10)

(3)Pi的确定——岩体位移

单元i对应的自由岩体位移Ui，地基基床系数ki，该单元受土体位移作用为Pi=DlkiUi，代入上式得到：

(11)

(12)

3.2 数值分析

选取距明挖边缘6.7m的雨水管(砼、DN700、埋深3.1m)进行模拟，管线采用壳单元模拟，管线和岩体之间设置面单元[9]，并考虑管线与岩体的共同作用。初始应力场云图如下：

图6 初始应力场云图

图7 基坑水平变形云图

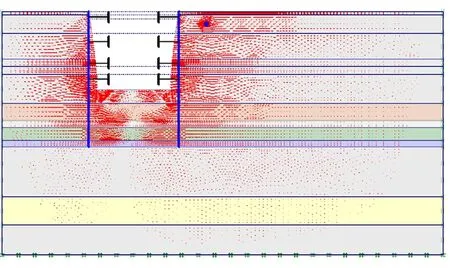
图8 基坑水平变形矢量

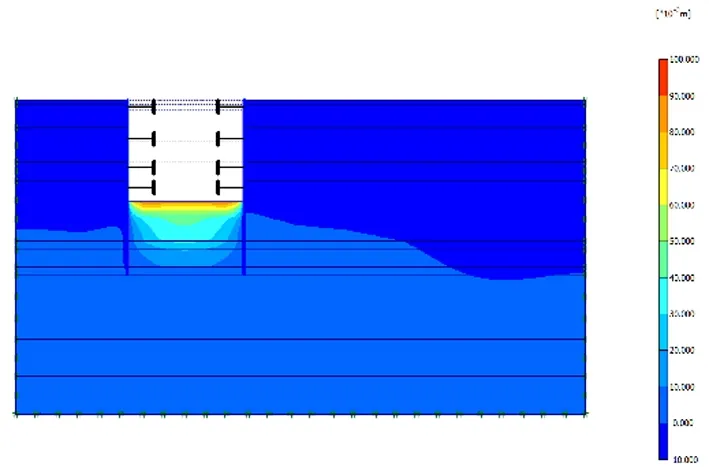
图9 基坑竖向变形云图

图10 基坑竖向变形矢量图

图11 围护结构水平变形图

从图7、图8水平变形矢量图可得，地铁基坑开挖影响最大沉降变形位置处于边缘8-10m处；其横向变形影响范围约35m左右，大约是地铁施工深度的2倍。从图10明挖围护支撑变形结果分析，从地铁车站明挖施工分析，中间层的围护支撑体系的水平位移最大，其最大变形为11.01mm，管线总位移为6.34mm，最大沉降为5.25mm。

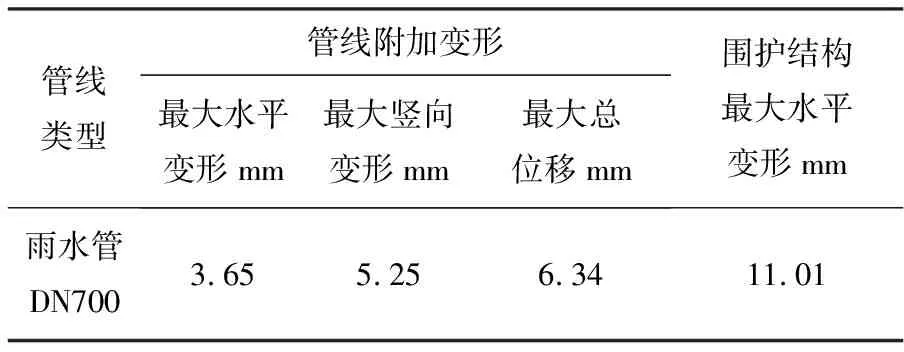
表3 有限元计算结果汇总

表4 邻近管线地表沉降监测结果

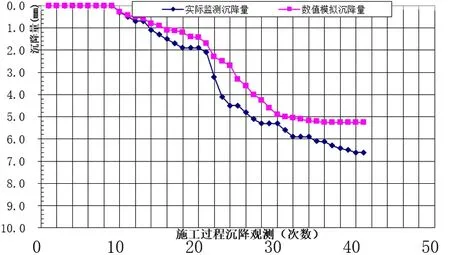
图12 明挖施工对邻近管线地表沉降监测结果对比图

从图12可分析，管线的变形与其埋深、距基坑边缘的远近、基坑的变形模式有密切的关系；参考福州地铁施工中规定，最大沉降控制标准是30mm，本车站主体基坑开挖引起的管线变形满足要求。

4 保护措施

地铁明挖施工中应加强监测，施工中监测数据突变时应采取加固措施，保证变形沉降、倾斜和裂缝降在可控范围之内。当位移值接近该管线允许值时，立即停止基坑开挖，如加大基坑支护刚度，辅以地基跟踪注浆等措施。具体措施为：

(1)对车站周围的地下水位加强监测，如有较大漏水应立刻停止降水，需立即对基坑外进行注水[10]，严禁长时间暴露开挖面。

(2)加强监测，并以监测数据的结果为依据，及时调整支护参数辅助施工。如周边邻近的管线变形超过规定的报警值，应立即采取有效的加固措施[11]。

(3)在基坑开挖过程中，遵循“先撑后挖，对称开挖”原则[12]，严禁超挖，如有超挖马上回填。

5 结 论

本文以福州某地铁项目明挖施工为实例，运用两阶段法及整体数值分析法分析了车站开挖过程中对邻近管线的安全稳定性影响，根据项目实施期间的实测数据相应分析，模型分析结果具有较高可信度，可用于类似项目基坑进行指导性施工，结论如下：

(1)根据两阶段分析法及整体数值分析法得出，随着地铁基坑开挖，基坑周边地表呈现为“凹槽型”变形，距其周边变形约8-10m位置出现较大沉降;直至明挖边缘35m左右逐渐消失，其横向变形影响规模约地铁施工纵深的2倍左右。

(2)本文基于两阶段分析法把基坑周边的管线模拟为弹性地基梁，将基坑开挖引起的土体自由场位移作为边界条件施加于地基梁上，取得管线和岩体的彼此作用的位移控制的简易公式，推导出地铁基坑开挖变形和管线变形的的数学计算模型，可用于施工过程中采取两阶段分析法的数学模型对管线沉降简单预测。

(3)本文依托福州地铁某车站基坑施工对邻近管线安全性影响，通过两阶段分析法、整体数值分析法结合实际监测数值对比，分析出明挖车站支撑体系结构变形呈现为中间大、两端小的“凸起型”，且最大位移量处于第二道支撑附近，为此在开挖过程中此处需加强处理。

(4)由数据分析出地铁基坑开挖施工引起的管线沉降规律及影响范围，为避免因基坑施工而导致安全事故，本文提出相应的加固措施，为地铁车站明挖施工控制提供理论支撑。