LBS中外包空间数据的kNN安全查询方法

梁丽莎 卢 来* 吴卫祖

1(广东海洋大学寸金学院 广东 湛江 524094) 2(广东海洋大学数学与计算机学院 广东 湛江 524088)

0 引 言

数据库外包是常见的云计算服务范例，数据所有者可以充分利用其存储和计算资源。为了减少成本，资源受限的公司可以将他们大量的数据外包给具有动态存储和计算能力的第三方服务提供商。云计算由于其方便性引起了较高的关注度，但是大量数据被不受信任的第三方控制会引起机密性和隐私性的安全问题。

移动设备和导航系统普遍使用基于位置服务(Location Based Service,LBS)，导致需要妥善管理的空间数据增加。日常生活中有大量用户使用LBS，他们以匿名的方式发起空间查询并在有效时间内收到响应。同样，数据所有者为了保护数据隐私性，不想将其透露给服务提供商(Service Provider,SP)，因此将数据外包给云服务提供商(例如：百度地图)。认证用户向SP发送信息查询请求时，数据所有者和用户都不想把真实数据透露给服务提供商。

在把空间数据库外包到云平台上时，必须考虑以下几点情况。对于恶意攻击者和服务提供商来说，数据库内容必须保持隐藏。通过数据加密可以简单地保护用户数据隐私，即数据所有者加密整个数据库，并且将加密数据(不带任何其他信息)发送给SP。在查询期间，认证用户从SP处获取所有的加密数据，然后解密并搜索需要的数据点。这样虽能保证安全，但是由于其产生的通信开销极高，尤其是当用户只需要一小部分数据点时，在实时应用中并不可用。

现有的保护外包数据的方法大部分采用空间变换机制[1-3]或者密码学技术[4-6]。然而大多数的保护机制都会在数据机密性和查询过程有效性之间权衡。为了解决这些问题，本文提出一种两层编码方法，先转换数据，然后对转换空间加密。此外，查询过程只需要在用户和云服务提供商之间通信一次就可实现。采用Hilbert空间填充曲线(用户定义曲线参数)来变换空间数据点。由Hilbert索引范围定义数据包列表，然后用顺序保留加密(Order-Preserving Encryption, OPE)技术[7]对列表加密，OPE支持在服务器处执行空间kNN查询。采用OPE的优势在于其将原始距离值隐藏，在SP处通过简单的对比来正确评估。另外，数据所有者向认证用户提供密钥，用转换密钥和加密密钥向SP发送编码查询，最后用OPE密钥解密查询响应。

云架构模型主要由三类实体构成，分别为：数据所有者(Data Owner,DO)，服务提供商(Service Provide,SP)和认证用户(Authorized User,AU)，如图1所示。DO外包其空间数据点，在外包给SP之前通过变换和加密数据库确保数据的安全性。AU利用变换密钥向SP发起加密的kNN查询。该查询在SP处在加密数据库上处理并将结果返回给用户。AU利用密钥解密查询响应来获取真实的查询结果。

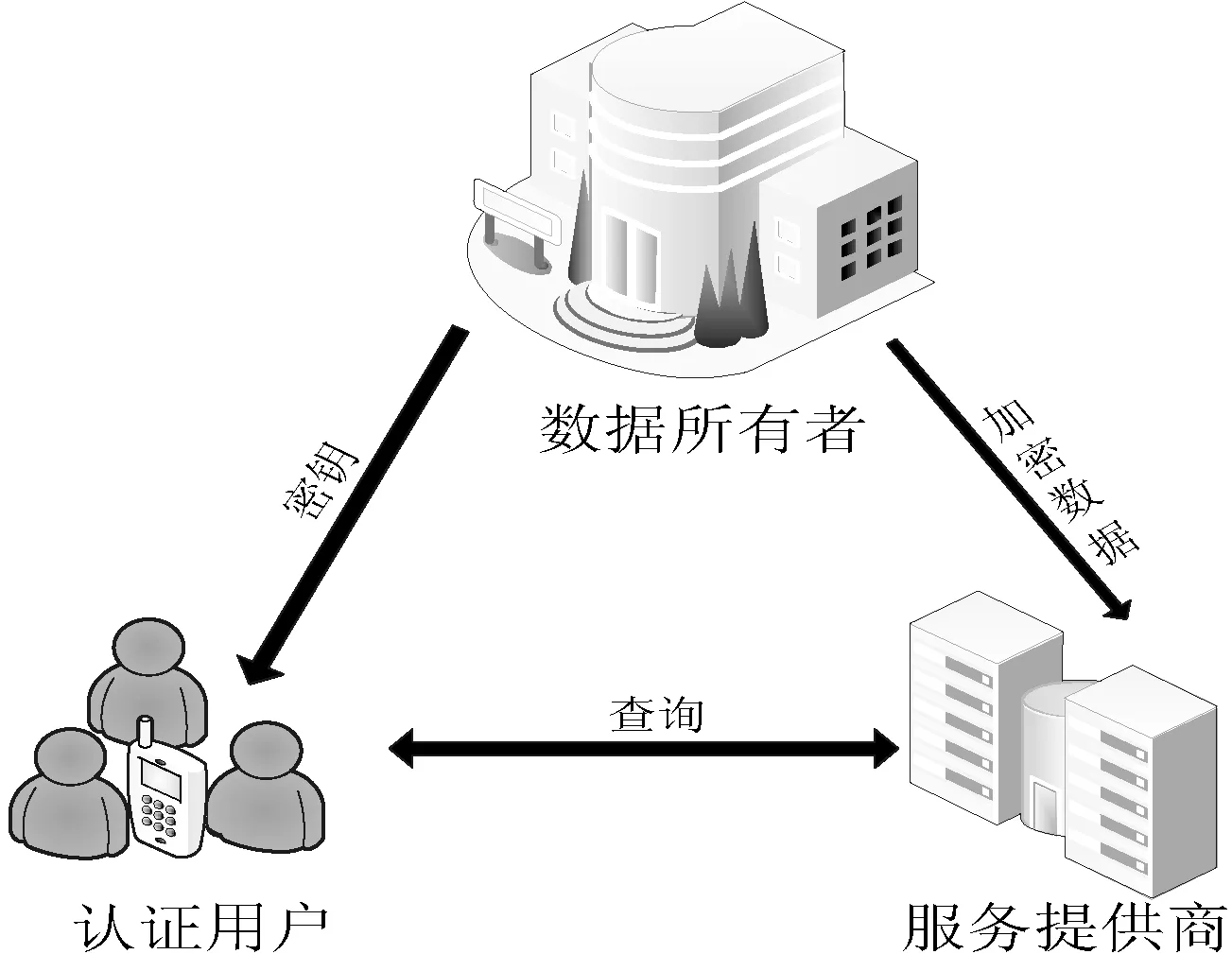
图1 云架构模型图

1 相关研究

移动设备和导航系统的大量应用使LBS迅速发展起来。文献[8-9]提出通过在SP处增加一个中间设备或者防干扰设备来确保安全性。该设备通过对传送的消息加密和解密来协助处理查询。假设在服务器端存在一个可信设备，文献[9]提出一种快速查找加密技术用于非顺序保留AES加密。数据库所有者先基于一维值建立一个B树，然后加密每一个节点级的记录来防御非受信任SP攻击数据。

然而，在用户数量越来越多的情况下，SP处单台设备服务每一个 AU已经不现实。为了解决这个问题，文献[4]提出一种基于密码的转换机制来确保二维数据的安全性：DO采用R*树架构来索引数据库并采用AES加密算法加密每一个节点；根据R*树服务器与用户之间的深度大小，查询过程需要多个回合，导致通信开销的增加；SP向AU发送加密的根节点，AU利用密钥解密节点，然后请求子节点与查询区域重叠，直到找到相应数据点的叶节点。

类似地，文献[5]提出一种基于Hilbert曲线转换的密码机制来平衡数据安全性和查询效率之间的关系。采用Hilbert曲线将数据局部聚类，并用AES加密转换数据。加密文件安全地存放在SP处。查询过程首先将整个加密文件发送至AU，解密之后搜索与查询内容相关的记录。但该方法后来被证明需要消耗大量的时间。

除上面提到的密码技术以外，学者还提出了基于空间位置分割和再分配的空间变换方法，如：空间层次划分(Hierarchical Space Division,HSD)、基于误差变换(Error-Based Transformation,ERB)和HSD/ERB混合变换[4]。文献[10]提出另一种空间变换机制，通过切边变换和路由变换提供数据安全性。然而，这些技术均需要保留原始空间点的坐标，并且假设攻击者能够获取原始点和变换空间中原始点坐标的背景信息，暴露了数据点附近的信息。

对用户而言，保证查询过程的即时性是LBS的关键，因此数据库外包必须使用低通信开销技术，需要对空间数据和查询区域进行编码。大多数现有的研究成果并没有利用SP的计算能力，基于此本文提出一种服务器端针对加密数据的安全有效的kNN查询方法来解决这一问题。

2 加密空间变换

为了保证空间数据的机密性，原始空间的二维数据点以两种方式隐藏：(1) 利用Hilbert空间填充曲线将空间中的二维点转换成一维点；(2) 利用OPE[11]加密生成的Hilbert单元值，然后用AES加密产生的数据点。变换密钥和加密密钥都通过SSL协议由DO直接发送至AU。

2.1 Hilbert数据包列表设计

首先将静态空间数据点分配到网格中，网格由Hilbert空间密钥[2](Hilbert Space Key,HSK)根据曲线生成。HSK={x0,y0,θ,n}，其中:(x0,y0)是曲线起始点，θ为曲线方向，n为曲线顺序。HSK支持单向转换，有可能出现两个或者多个点在曲线中有相同的单元索引。

DO创建Hilbert数据包列表(Hilbert Packet List,HPL)过程如下：首先，为空间中的每个数据点在网格中分配一个Hilbert单元值。其次，基于单元值将数据点存储到数据包中，每个数据包包括：Ps(数据包起始Hilbert索引)，Pe(数据包结束Hilbert索引)和Pc(数据包原始空间点固定值)。Ps、Pe分别代表数据包中起始和结束数据点的位置，Pc由每个数据包存储的数据点的数量c决定。

当曲线顺序n为3，c为4时，HLP示意图如图2所示。第一个数据包Ps=0，以c个数据点填充Pc，Pe是数据包中第c个目标的单元索引。空Hilbert索引值表示没有分配空间点，其一般不会在HPL中出现，除非索引在数据包填充完成之前发生冲突。

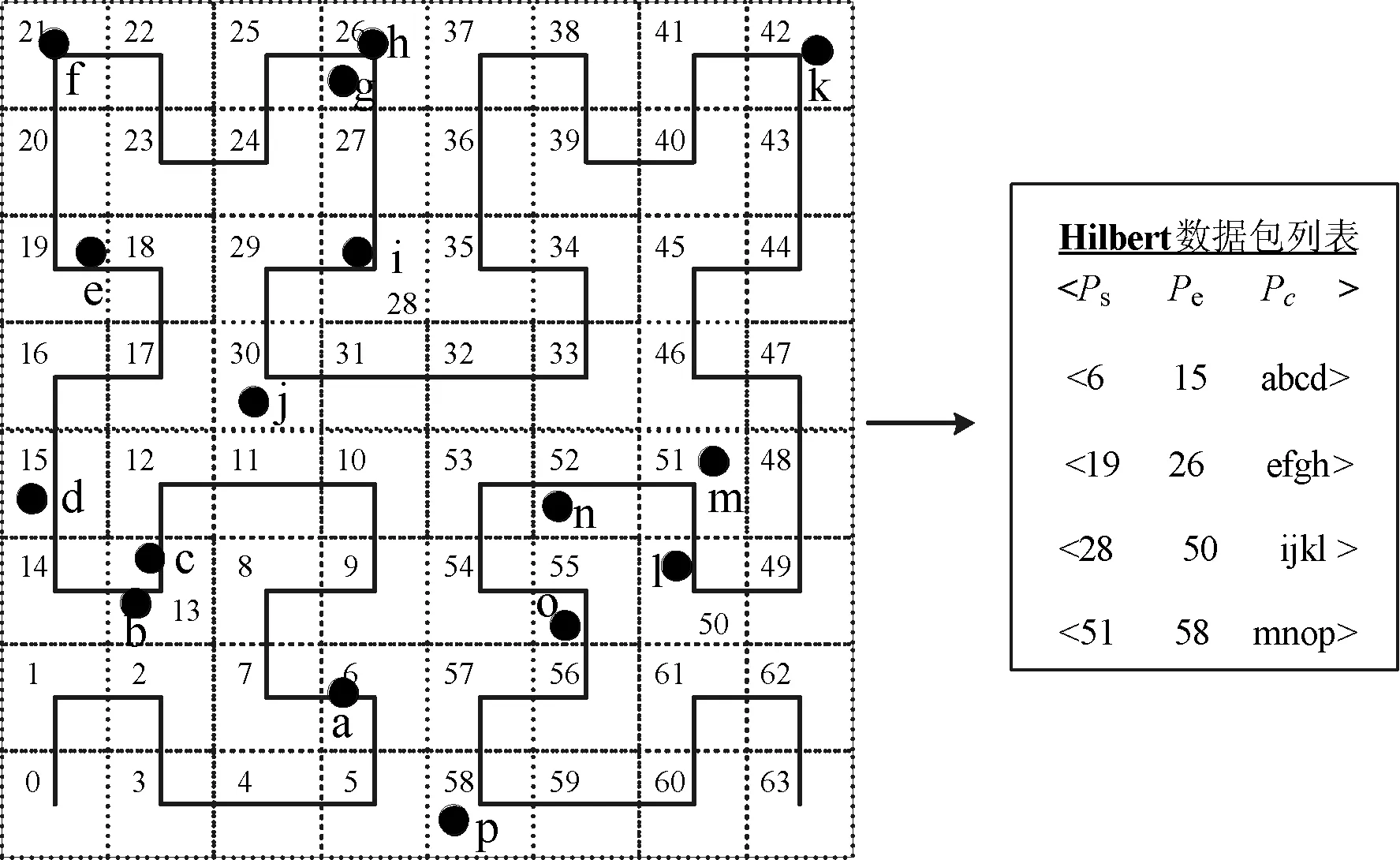
图2 Hilbert空间变换和Hilbert数据列表

2.2 OPE

为了进一步对空间数据进行编码，在将HLP发送至SP之前，DO采用OPE技术对其加密。这保证了数据不会被SP泄露给第三方中介。此外，为了阻止数据的非认证访问，SP在使用数据之前没有能力解密数据。因此，采用OPE机制确保明文数据的顺序以加密的方式保存，并可以在加密数据上评估查询。最后，DO向AU发送OPE密钥来加密查询Hilbert单元，并将SP返回的查询结果解密。

3 kNN查询过程

本文主要关注LBS中应用最为广泛的二维空间kNN查询。评估期间，将kNN查询转换成一组一维Hilbert单元值(部分或者全部与周围区域重叠)。SP和AU均参与处理查询过程。数据点及其Hilbert单元值放入HPL，经加密之后存放在SP。AU通过定义查询点发起kNN查询。通过定义圆形区域(Circular Region,CR)可以发现查询点周围的k个邻近点。AU将查询转换成一组落入该区域的加密Hilbert单元值。利用OPE密钥加密查询请求然后将其发送至SP。SP通过比较加密的Hilbert起始和结束单元值范围，将相关的加密返回给AU。AU利用密钥解密返回的结果数据点，通过寻找查询点的k个临近点生成真实的查询结果。

kNN查询过程如图3所示。查询请求由Hilbert值重叠的CR组成。发送的Hilbert值相当于HPL的起始和结束元组。两个元组中包含的加密数据点集返回AU，用户从中取出需要的k个点。

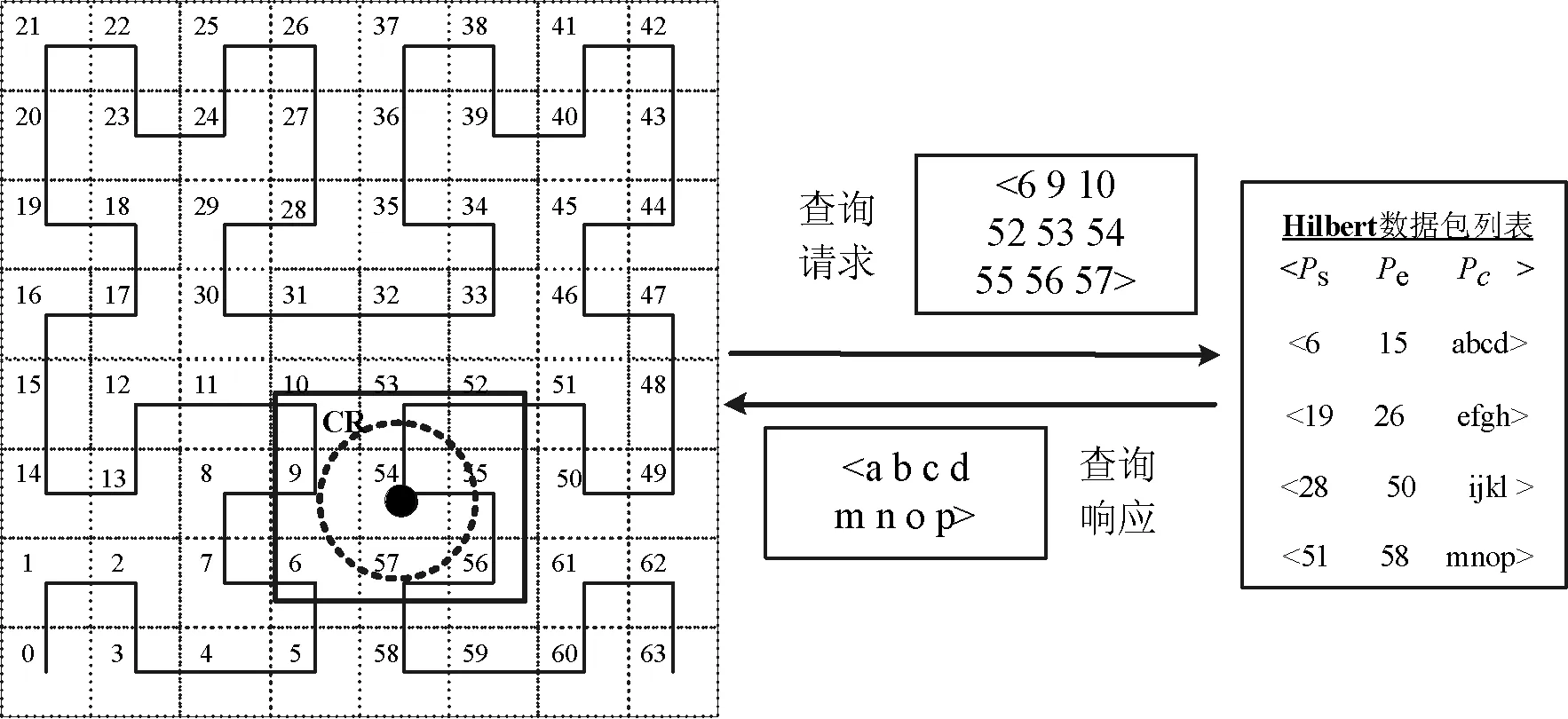
图3 kNN查询交换过程

算法1列出了空间kNN查询的处理过程。已知查询点Q和点Q周围的圆形区域CR。步骤2)中Hilbert单元与CR重叠生成查询区域；步骤3)-步骤5)中加密查询Hilbert单元并发送至SP；步骤6)-步骤12)、步骤15)在SP处完成。与查询Hilbert单元值匹配的元组返回至AU。如果返回数据点的数量小于k，则重新定义个更大范围的CR并另外发送Hilbert单元值给SP，之后的处理方法同上。此外，步骤16)-步骤20)中，空间数据点在AU处加密，获得Q周围的k个最近的数据点。

算法1空间kNN查询

输入：查询点Q。

输出：kNN结果为k个空间数据点。

1) while (k>size(Result))

2) QueryCells=cells contained in CR around Q

3) for all (c∈QC)

4) HilbertCells=HilbertCells∪(encrypt) Hilbert(c)

5) end for

6) for all (p∈HPL)

7) while (HilbertCells≤Psi)

8) if (HilbertCells∈[Psi,Pei])

9) Result=Result∪Pci

10) end if

11) end while

12) end for

13) Increase the radius of circular region, CR

14) end while

15) Return Result to AU

16) for all (r∈Result)

17) rD=Decrypt r

18) distNN=Compute distance between Q and rD

19) end for

20) kNNResult=FindkNN(distNN)

4 实 验

通过实验对该方法进行有效性评估，采用多个参数来衡量Hilbert变换效果，均展示出快速的系统响应。实际环境为Intel Core i7-3770 CPU @ 3.40 GHz。以两个不同大小的真实空间数据集[12]为例：(1) 奥尔登堡市(Oldenburg City,OC)道路网，包含1 104个点；(2) 美国东北部(North East,NE)，包含123 593个点。

4.1 Hilbert空间密钥

Hilbert空间变换利用HSK对空间数据库进行编码。为了突出HSK的全面性，通过改变Hilbert曲线顺序来分配数据点。n值越大表示网格粒度越大，安全性越高。分配给每个Hilbert索引值的平均点数量如图4所示。随着n的增加，每个Hilbert索引值的平均点数量急剧减少。对于数据集OC和NE，当n=5和n=8时，平均点数量小于2。

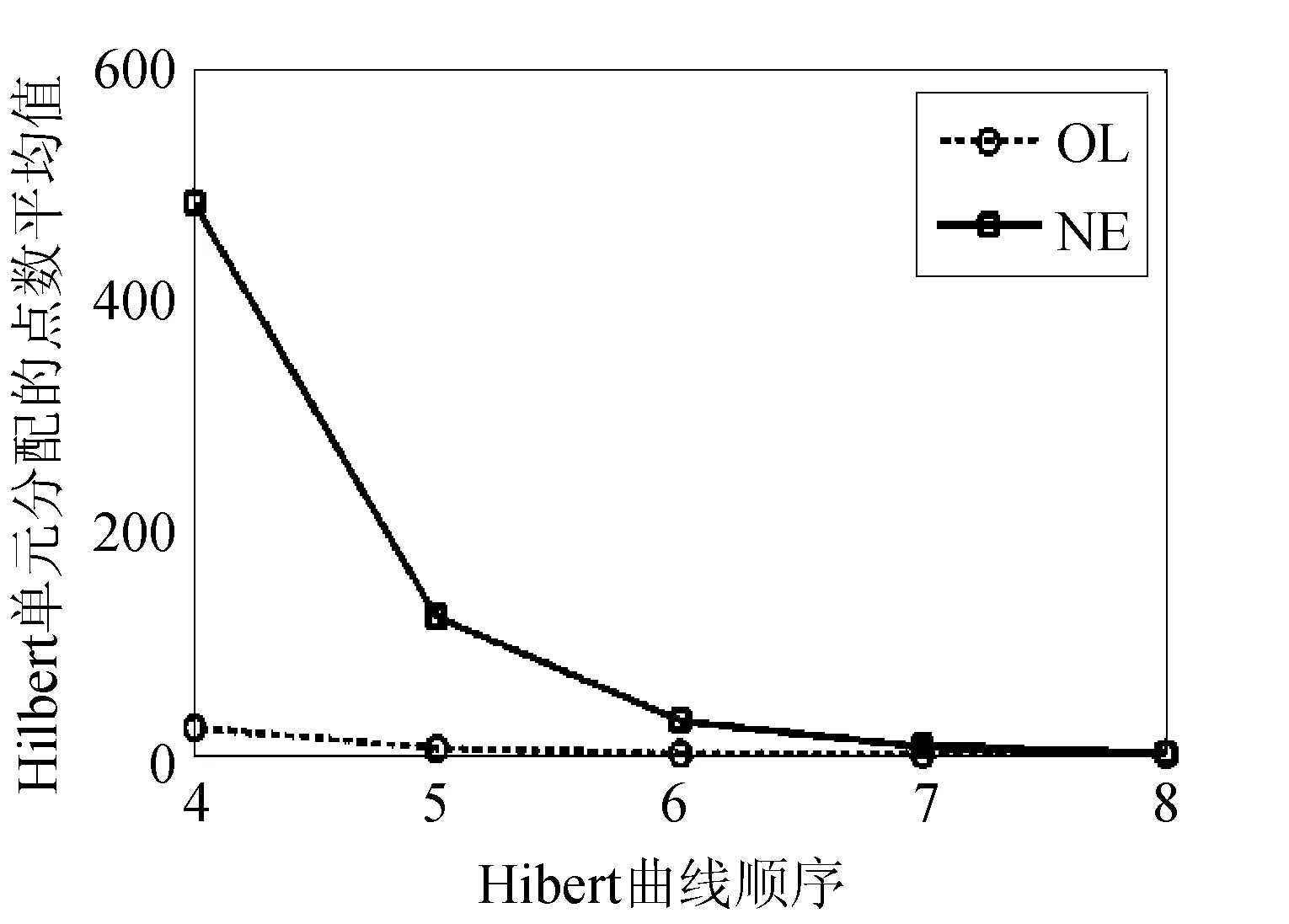
图4 Hilbert曲线顺序与点数平均值关系图

4.2 空间kNN查询处理时间

两个数据集中SP处理kNN查询(如搜索加密HPL)的消耗时间如图5所示，每个kNN查询的查询点从区域空间随机生成。不同查询大小的查询时间均为毫秒级别。k值越小，查询时间越短，且两个数据集性能趋势大致相同。

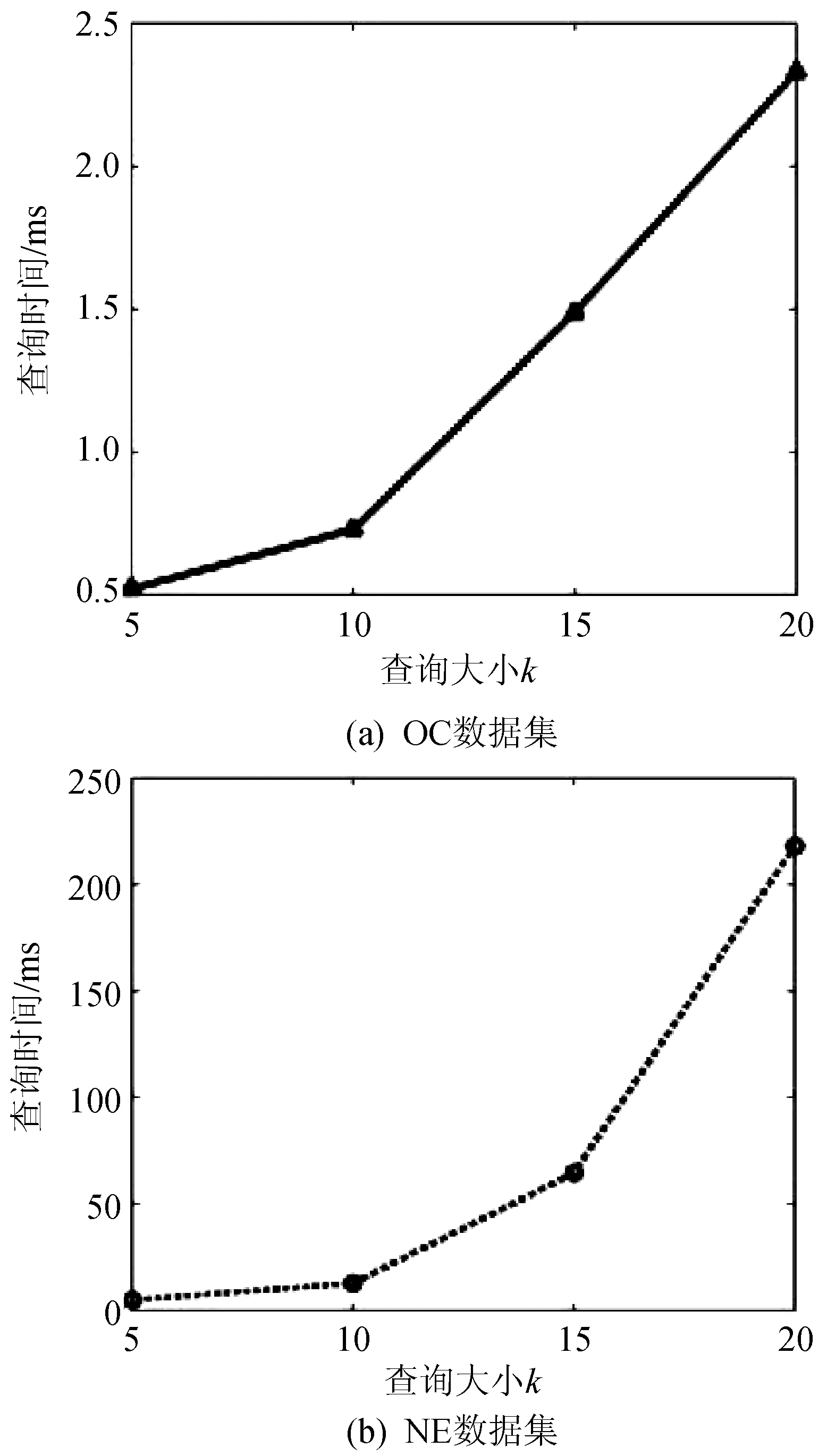
图5 kNN查询大小与查询处理时间关系图

4.3 kNN查询通信开销

实验中根据不同的k值生成随机kNN查询，并测量在此交换过程中SP和AU之间的数据量，通信开销包括：1) AU利用HSK将查询区域转换成一组Hilbert单元值并将其发送至服务器；2) SP搜索HPL中相应的空间点并返回加密结果，用4个字节代表Hilbert单元值，每个空间点为16字节。OC和NE中，k取4种不同大小值，100次查询的平均通信开销如图6所示。可以看出，随着查询大小的增加，发送的Hilbert单元值和返回数据点也增加，通信开销呈线性增长。当k=20时，与同样采用AES加密的CRT技术[4]相比，该方法响应时间比CRT技术快了1.75倍。

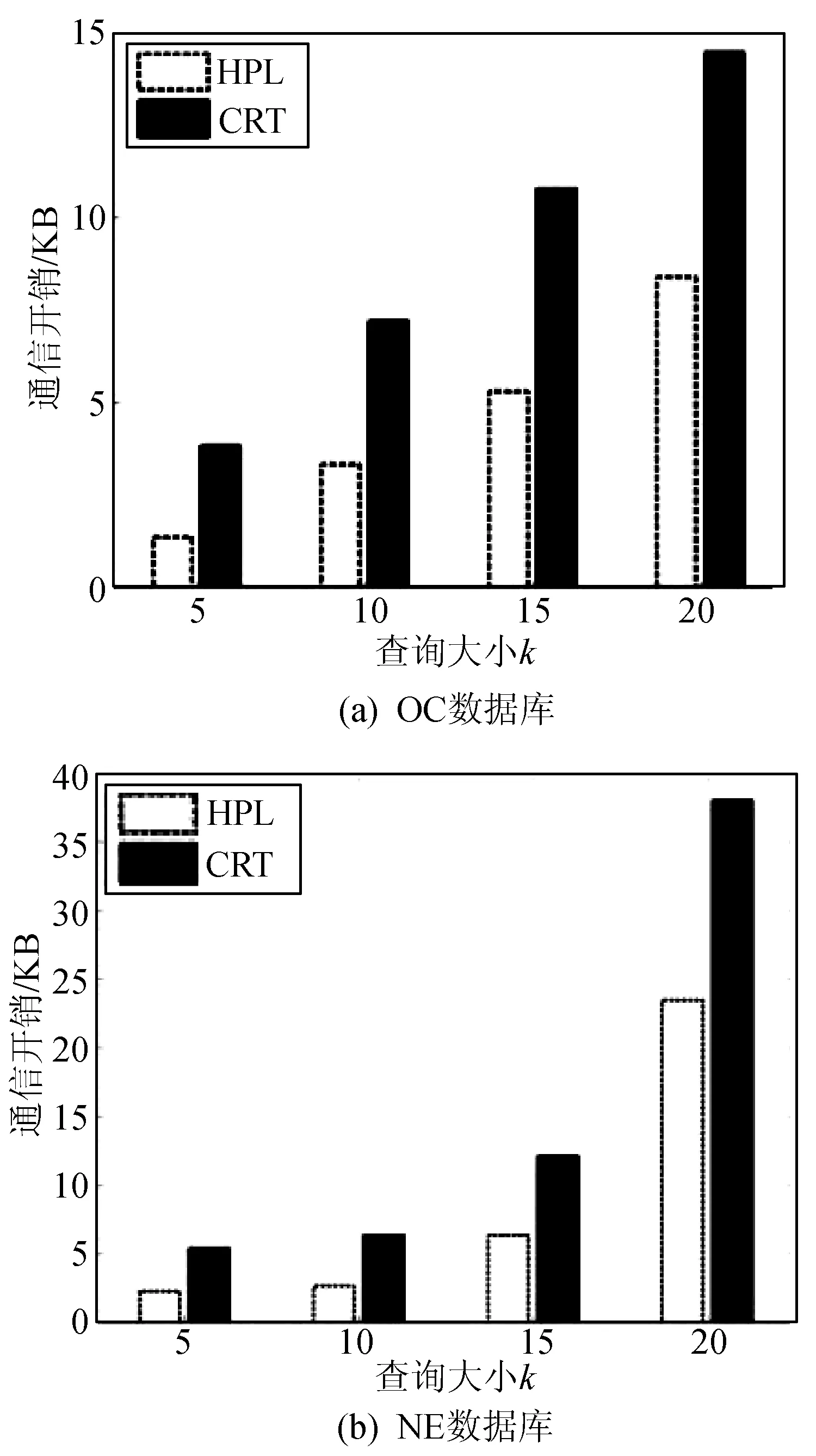
图6 查询大小与通信开销关系图

5 结 语

云计算服务可以通过在服务器端虚拟存储和计算资源，向认证用户提供数据的方式将数据集外包。为了平衡服务器端数据的机密性和查询的有效性，本文提出一种安全有效的kNN查询方法。利用Hilbert曲线变换空间数据集，并引入顺序保留加密方法变换数据来提高安全性。实验证明该方法比现有的加密方法性能更好。该双重变换方法不仅为数据提供保护，而且使认证用户能及时收到空间kNN查询回复。