基于改进模糊决策粗糙集的最小化决策代价特征选择算法

王 鹏 王玉红

(赤峰学院数学与计算机科学学院 内蒙古 赤峰 024000)

0 引 言

决策粗糙集模型是目前粗糙集理论的重要研究分支，它最早由加拿大著名学者Yao[1-2]提出。决策粗糙集模型以决策代价为基础，通过最小化决策代价原则来进行目标概念的粗糙近似，因此具有很高的实用价值。目前决策粗糙集模型已成功应用于数据分类[3]、数据聚类[4-5]、图像处理[6]以及个性化推荐[7]等领域中。

由于决策粗糙集模型的优越性，目前已进行了大量的改进和推广。例如，为了适应不完备型的数据集，Liu等[8]在不完备信息系统下提出了改进的决策粗糙集模型。对于分布式的数据集，Lin等[9]提出了基于多源信息系统的决策粗糙集。在多粒度数据环境下，Qian等[10]提出了多粒度决策粗糙集模型，刘丹等[11]学者在Qian等模型基础上，提出了一种改进的多粒度决策粗糙集，称之为不完备邻域多粒度决策粗糙集。在多类别的数据集下，Zhou[12]提出了基于多类的决策粗糙集模型。Li等[13]在数值型数据集下提出了邻域决策粗糙集模型。另一方面，在模糊集的数据环境下，学者们也对传统的决策粗糙集进行了相应的推广。Sun等[14]提出了模糊决策粗糙集模型，该模型的提出标志着决策粗糙集模型的适用范围进一步扩大。在Sun等模型的基础上，Song等[15]在模糊决策粗糙集中提出了最小化决策代价的特征选择算法。

然而，Sun等[14]提出的模糊决策粗糙集模型未考虑数据集中噪声数据带来的影响，使得在模糊数据相似性的刻画方面，存在一定的局限性。这促使本文对其进行改进，进一步提升模糊决策粗糙集对噪声数据的容忍性能。

在粗糙集中，通过对二元关系设置一定的限定阈值[16]，可以提高二元关系对噪声数据的容忍性能。本文采用类似的研究方法， 在模糊决策粗糙集的模糊相似关系中，引入一个阈值，提出了一种改进的模糊相似关系。通过这种模糊相似关系，对Sun等的模糊决策粗糙集进行重新构造，提出了一种改进的模糊决策粗糙集模型。特性选择又称为属性约简，是粗糙集理论的重要应用[17-18]。在决策粗糙集中，基于最小化决策代价的特征选择是其研究的重点[13, 15]。本文在所提出的改进模糊决策粗糙集基础上，根据不同的特征选择策略，设计出了两种最小化决策代价的特征选择算法，分别为基于属性增加策略的特征选择和基于属性删除策略的特性选择。实验结果表明，所提出的两种最小化决策代价特征选择算法均比原始模糊决策粗糙集的特征选择算法具有更高的优越性，同时在两种特征选择算法中，基于属性增加策略的算法具有更好的特征选择性能。

1 基本理论

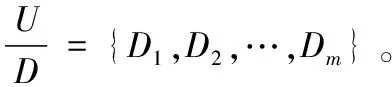
在论域U中，设F为论域U至区间[0,1]上的映射，即F:U→[0,1]，对于∀x∈U有F(x)∈[0,1]，那么称F为U上的模糊集，同时称F(x)为对象x的模糊隶属度。

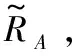
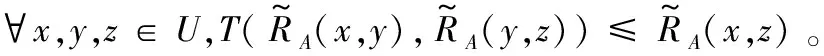
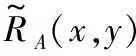
考虑信息系统S=(U,C∪D)，设属性子集∀A⊆C，通常∀x,y∈U之间的模糊相似度采用高斯核函数[14]进行计算：

(1)

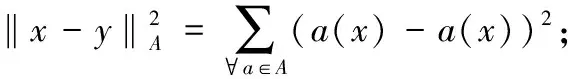
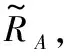
(2)

式中：∑为模糊集的Zadeh记法。

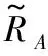
(3)

在决策粗糙集中，设对象集X⊆U表示某种状态，记论域U中的状态集为Ω={X,Xc}，其中Xc表示X的补集。考虑对象x∈U的动作集为Δ={aP,aB,aN}，这里的aP、aB和aN分别表示对象x标记为状态X的POS(X)、BUN(X)和NEG(X)三种动作，其中：POS(X)为对象集X的正区域；BUN(X)为对象集X的边界域；NEG(X)为对象集X的负区域[1-2]。

另外，对于状态集Ω={X,Xc}和动作集Δ={aP,aB,aN}，定义它们之间的决策代价矩阵如表1所示。其中λPP、λBP和λNP分别表示对象x处于状态X而采取aP、aB和aN三种动作的决策代价；λPN、λBN和λNN分别表示对象x处于状态Xc而采取aP、aB和aN三种动作的决策代价。

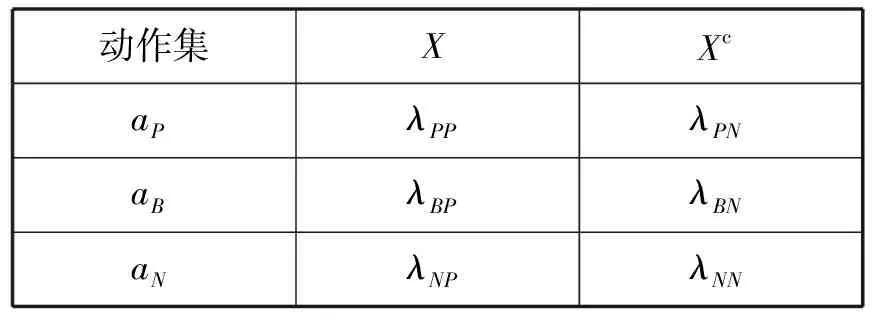
表1 决策代价

基于贝叶斯决策理论，Yao[1-2]根据最小化决策代价提出了决策粗糙集模型，Sun等[14]在Yao的基础上，将传统的决策粗糙集在模糊集视角下进行推广，提出了模糊决策粗糙集模型。

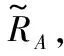
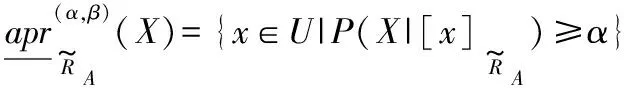
(4)

式中：α=max{η1,η2,η3};β=min{η1,η2,η3}。

(5)

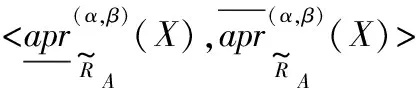
2 改进的模糊决策粗糙集模型

Sun等[14]提出的模糊决策粗糙集模型，在处理连续型和模糊型的数据集方面发挥了重要的作用。然而在实际应用中，数据集往往包含了很多的噪声数据，这些数据的存在对已有的粗糙集模型产生了很大的影响。

在经典的模糊决策粗糙集模型中，对象之间的相似程度通过模糊相似关系的模糊相似度来刻画，无论对象之间的相似程度如何，模糊相似关系都能给出确定的模糊相似度值，然而由于噪声数据的存在，本来两个对象之间是不具有相似性的，而模糊相似关系也对其赋予了相应的模糊相似度，这对模型的粗糙计算产生了一定的影响。因此对于模糊相似度较小的值，本文考虑通过引入一个限定阈值来改进对象之间的模糊相似关系。

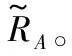
(6)

定义4表明，对象之间的高斯核函数值低于阈值ε，那么这两个对象之间的模糊相似度为0，即认为相似度很小的对象之间不具有相似性。特别地，当ε=0时，定义4定义的改进模糊相似关系退化为原始的模糊相似关系；当ε=1时，所提出的改进模糊相似关系退化为传统的等价关系。因此，本节所提出的改进模糊相似关系为传统模糊关系和传统等价关系的进一步推广，而传统的模糊关系和传统的等价关系为所提出改进模糊相似关系的特例。

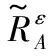
(7)

类似于原始的模糊决策粗糙集模型，这里同样设对象集X⊆U表示某种状态，记论域U中的状态集为Ω={X,Xc}。考虑对象x∈U的动作集为Δ={aP,aB,aN}。

另外，对于状态集Ω={X,Xc}和动作集Δ={aP,aB,aN}，定义它们之间的决策代价矩阵同样如表1所示。

(8)

其中：

若进行决策规则代价最小化，那么有：

(1) 当对象x采取aP代价最小时，即CostP(x)≤CostB(x)且CostP(x)≤CostN(x),则x∈POS(X)。

亦即：

且：

(2) 当对象x采取aB代价最小时，即CostB(x)≤CostP(x)且CostB(x)≤CostN(x),则x∈BUN(X)。

亦即：

且：

(3) 当对象x采取aN代价最小时，即CostN(x)≤CostP(x)且CostN(x)≤CostB(x),则x∈NEG(X)。

亦即：

且：

综上所述可以得到：

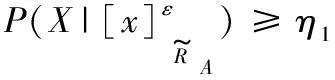
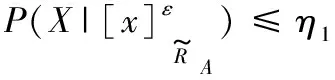
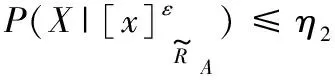
其中：

特别地，当决策代价满足如下关系时：

有0≤η2<η3<η1≤1，那么决策规则可以进一步表示为：

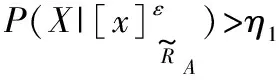
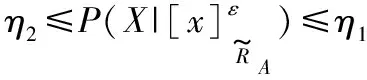
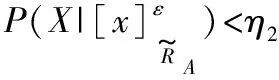
根据上述推导的η1、η2和η3结果，类似于原先的模糊决策粗糙集模型[14]，接下来在改进模型相似关系的基础上提出对应的模糊决策粗糙集模型，具体如定义5所示。

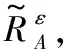
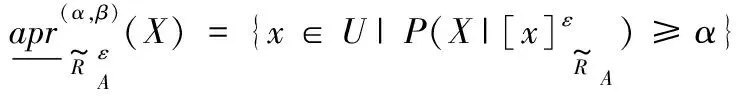
(9)

式中：α=max{η1,η2,η3};β=min{η1,η2,η3}。

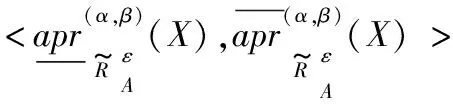
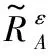
(10)

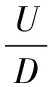
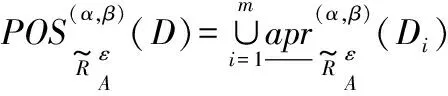
(11)

模糊决策粗糙集表明，在给定决策代价矩阵和模糊相似关系的情况下，对于所给出的目标决策集可以将论域划分成三个子区域，其中：正区域中的对象表明属于该决策集；负区域中的对象表明不属于该决策集；边界域中的对象不确定是否属于该决策集，暂不进行决策。

对于模糊决策粗糙集将论域U划分的三个区域集，可以分别得到三个区域中对象进行区域划分时所产生的代价。

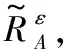
(1) 正区域：

(12)

(2) 边界域：

(13)

(3) 负区域：

(14)

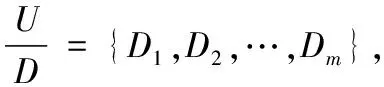
(1) 正区域：

(15)

(2) 边界域：

(16)

(3) 负区域：

(17)

同时，根据决策属性集D下三个划分区域的决策代价，可以进一步得到整个信息系统在特定决策代价矩阵和改进模型相似关系下的决策总代价，即决策总代价表示为：

(18)

3 最小决策代价特征选择算法

在传统的粗糙集模型中，由于信息系统的正区域、边界域和负区域随着属性集满足单调性变化，因此通过这三个区域来设计信息系统的特征选择算法[16-18]。而对于决策粗糙集模型，三个区域变化的单调性并不满足，由于决策粗糙集模型建立在决策代价的视角上，因此学者们在其基础上提出信息系统的最小化决策代价特征选择。同样，本文将在所提出的改进模糊决策粗糙集模型的基础上，提出对应的最小化决策代价特征选择算法。

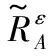
(19)

(20)

式(19)表明信息系统在特征子集下的决策代价不超过属性全集的决策代价，式(20)表明该特征子集是最小的，即该特征集的任意子集，其决策代价都比该特征集要高，也就是说特征约简集不包含任何冗余属性。

目前的研究已经表明，我们无法通过遍历每个属性子集来寻找特征约简集，只能通过特定的算法找出最接近的解。在目前的研究中，启发式搜索被认为是一种最有效的方法[19]，它的主要思想是对信息系统中的属性构建重要度评估函数，然后通过该函数进行启发式搜索，从而得到最终结果的近似解。类似于其他学者的相关构造方法，本文针对改进的模糊决策粗糙集模型，提出两种相应的属性重要度评估函数。

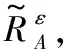
(21)

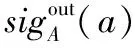
(22)

在基于粗糙集理论的特征选择研究中，启发式搜索特征子集主要有两种方式[19]：第一种为添加式启发式搜索，即从空集开始，通过属性重要度评估函数搜索属性，将满足条件的属性添加入约简集中，直到满足终止条件而结束；第二种为删除式启发式搜索，即从属性全集开始，通过属性重要度评估函数搜索属性，将满足条件的属性从属性全集中删除，直到满足终止条件而结束。基于这两种搜索方式，接下来本文设计出两种对应的最小化决策代价特征选择算法，具体如算法1和算法2所示。

算法1基于改进模糊相似关系的决策粗糙集最小化决策代价特征选择算法(属性增加策略)

输入：信息系统S=(U,C∪D)，决策代价矩阵，阈值ε。

输出：特征约简集red。

步骤1初始化red←∅。

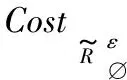
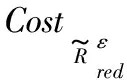
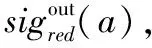
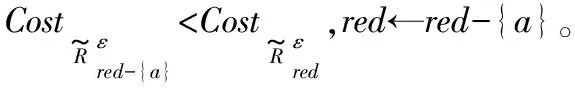
步骤6返回特征约简集red。

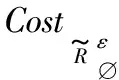
算法1中，设对象的数量为n，属性的数量为m，那么整个算法1的时间复杂度为O(m2·n2)。

算法2基于改进模糊相似关系的决策粗糙集最小化决策代价特征选择算法(属性删除策略)

输入：信息系统S=(U,C∪D)，决策代价矩阵，阈值ε。

输出：特征约简集red。

步骤1初始化red←AT。

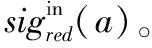
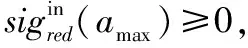
步骤4返回特征约简集red。

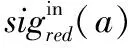
算法2中，设对象的数量为n，属性的数量为m，类似于算法1，整个算法2的时间复杂度同样为O(m2·n2)。

4 实验分析

对于本文提出的改进模糊决策粗糙集最小化决策代价特征选择算法，本节将通过进行一系列实验来验证其有效性，其中进行实验的硬件环境配置为主频3.4 GHz的i7 6700 CPU，8 GB DDR4内存，算法运行的软件环境为MATLAB 2010b。同时，实验中所使用的数据集均来源于UCI，具体如表2所示，由于这些数据集均为实际应用采集所得到，会包含一定的噪声数据。此外，为了构造模糊相似关系，表2中的所有数据集均为连续型的属性值。

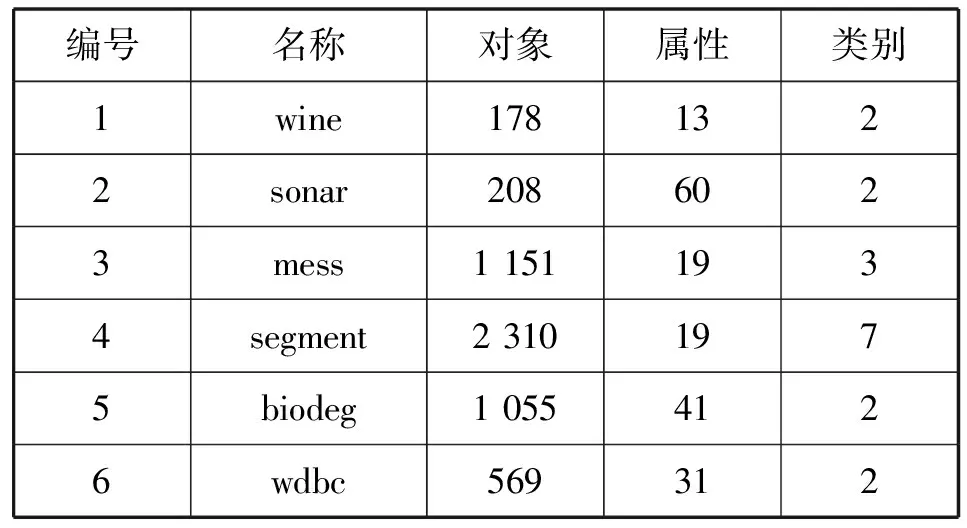
表2 实验数据集

实验中模糊相似关系的构建主要通过高斯核函数来进行计算，为了消除数据集属性量纲带来的影响，在计算前已将属性值进行标准化处理，同时在高斯核函数中，选取σ=1进行计算。对于表1中所示的决策代价矩阵，本实验按照0<λBN<λPN≤1和0<λBP<λNP≤1进行随机设定，并且λPP=0、λNN=0。

在本文所提出的改进模糊相似关系中，包含了参数阈值ε，它同时也是本文算法1和算法2的入参，由于阈值ε的取值不同对模糊相似度的计算产生很重要的影响，进而影响算法1和算法2的性能，因此选择合适的取值至关重要。接下来将通过实验来确定合适的参数值，实验的思路是通过取不同的ε值分别对多组数据集进行实验，然后选择具有较好实验结果的ε值。由于在多组数据集上进行实验，因此该ε值具有一定的一般性。让ε在区间[0,0.3]以0.02为间隔进行取值，每个取值对所有数据集进行算法1和算法2的最小化决策代价特征选择，其特征子集的决策代价结果如图1所示。

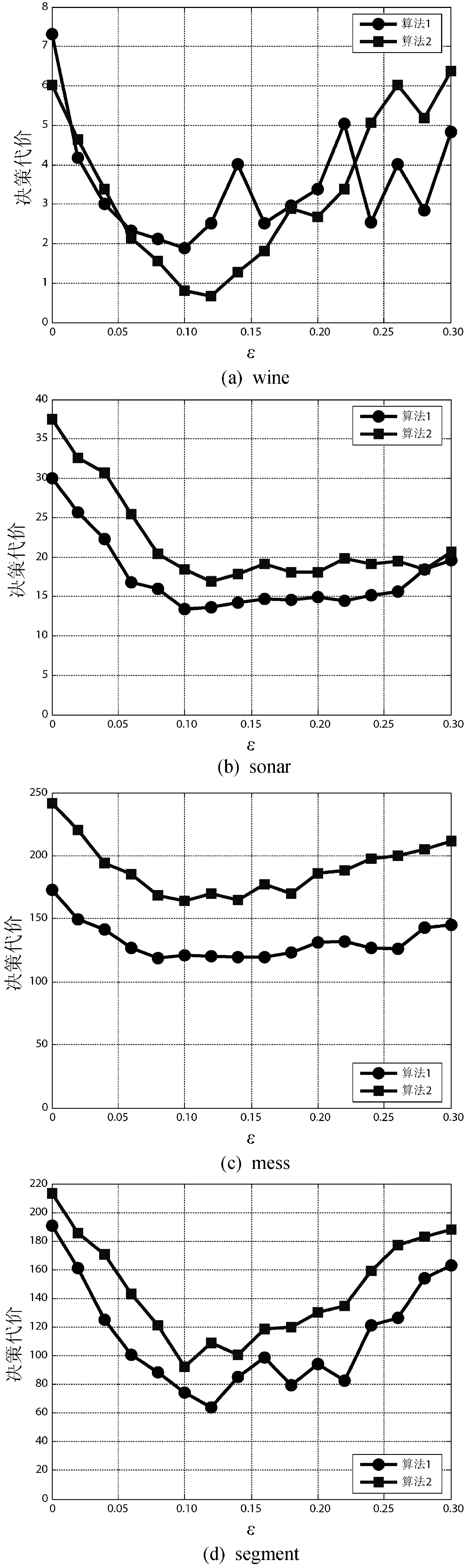
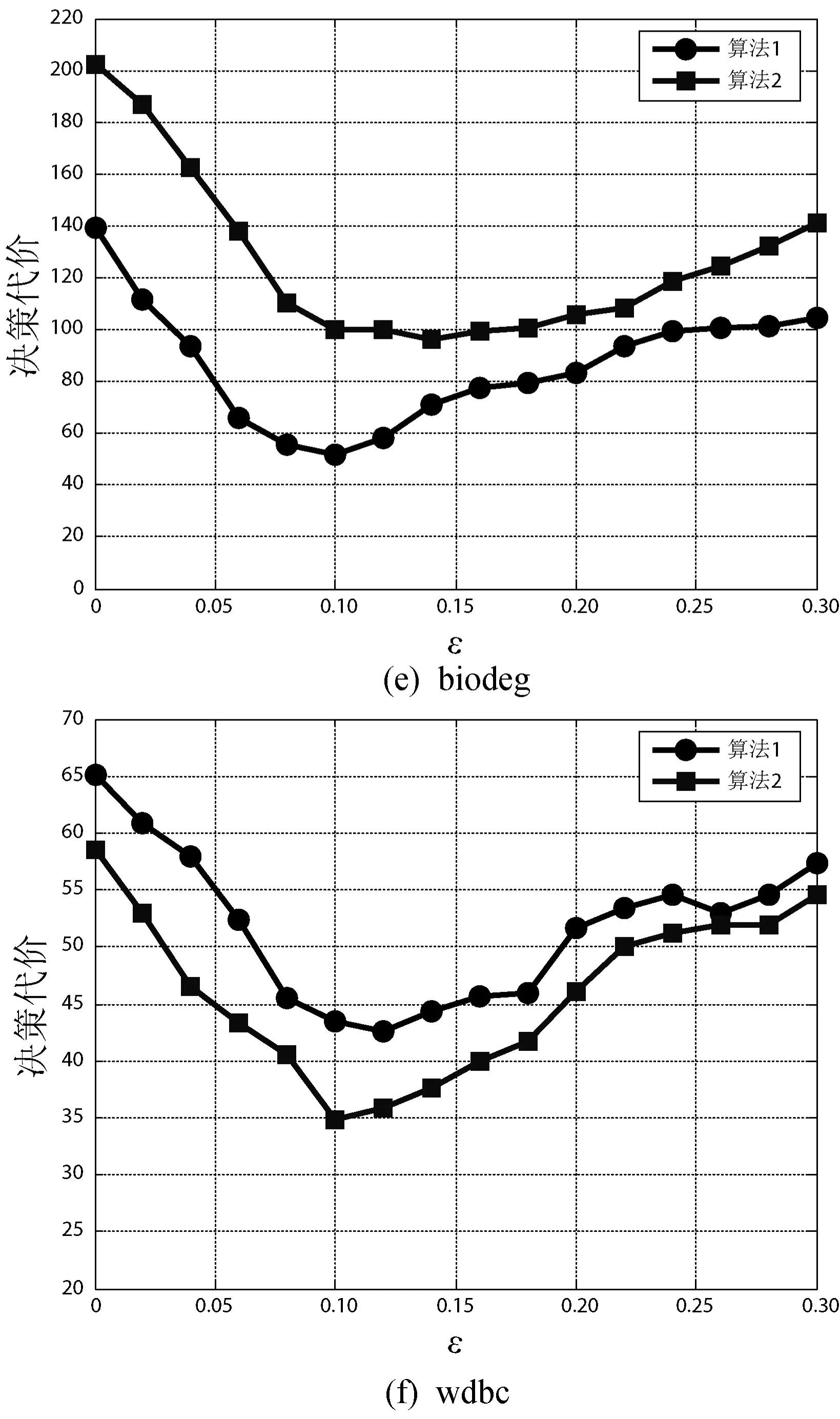
图1 各个数据集下不同阈值ε的实验结果

观察图1中每个数据集的实验结果，可以发现当ε取值为0.10～0.14时，其算法得到决策代价最小。本实验选择ε=0.12进行实验。

为了验证所提出的最小化决策代价特征选择算法具有更高的优越性，接下来将与原始的模糊决策粗糙集特征选择算法[15]对表2中的数据集进行实验对比。记原始的模糊决策粗糙集最小化决策代价特征选择算法为对比算法，其中两类算法采用相同的决策代价矩阵，最终得到的特征约简集决策代价结果如表3所示。

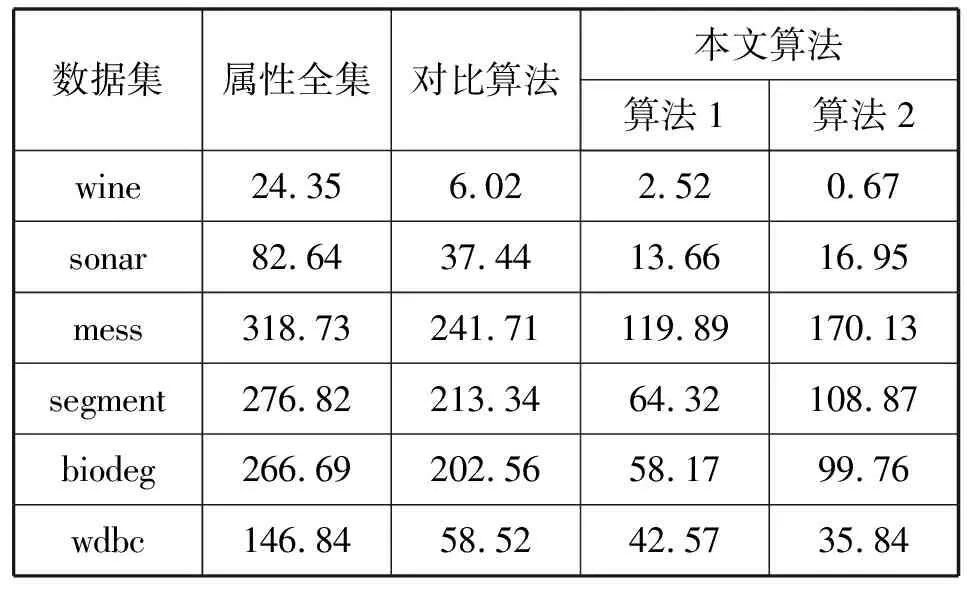
表3 特征约简集决策代价比较

观察表3的实验结果可以看出，本文算法得到的决策代价与对比算法得到的决策代价均小于属性全集的决策代价，这说明了从代价的角度，数据集中的冗余属性是普遍存在的，这也证明了对数据集进行特征选择的重要性。比较本文算法与对比算法的实验结果，可以发现本文算法在所有数据集下得到的决策代价都更小，这证明了改进后的模糊相似关系具有更好的模糊度量效果，通过引入阈值ε可以提高数据的模糊关系刻画。同时比较本文的算法1和算法2，可以发现算法1在大部分数据集下的决策代价更小，即属性增加策略的搜索方式得到的实验结果更优。

算法效率是评估特征选择算法优越性的重要指标，本实验让本文算法与对比算法对每个数据集重复进行10次特征选择实验，记录各算法每次进行实验所需的时间，并计算出每个算法对应的平均时间，其实验结果如图2所示。

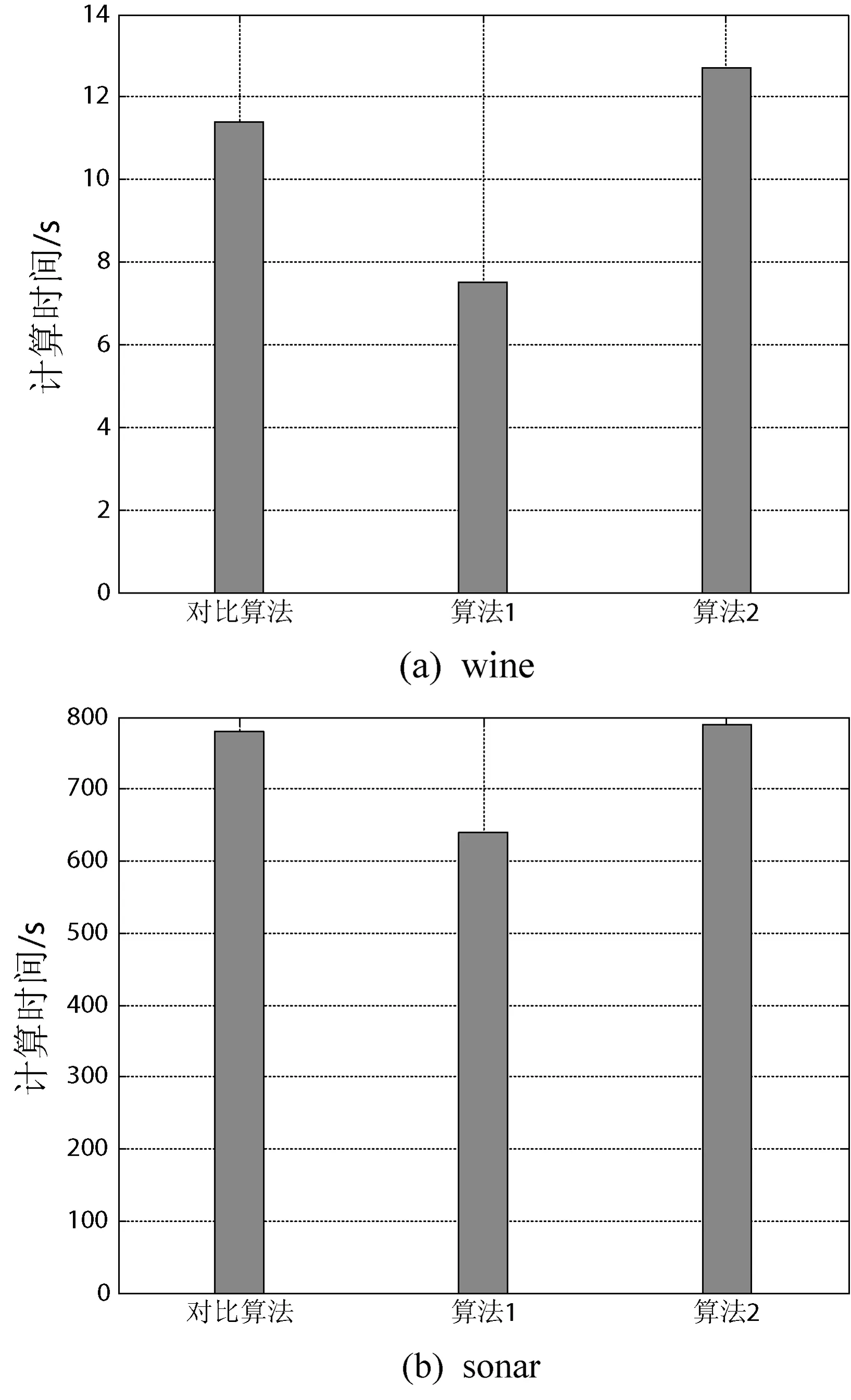
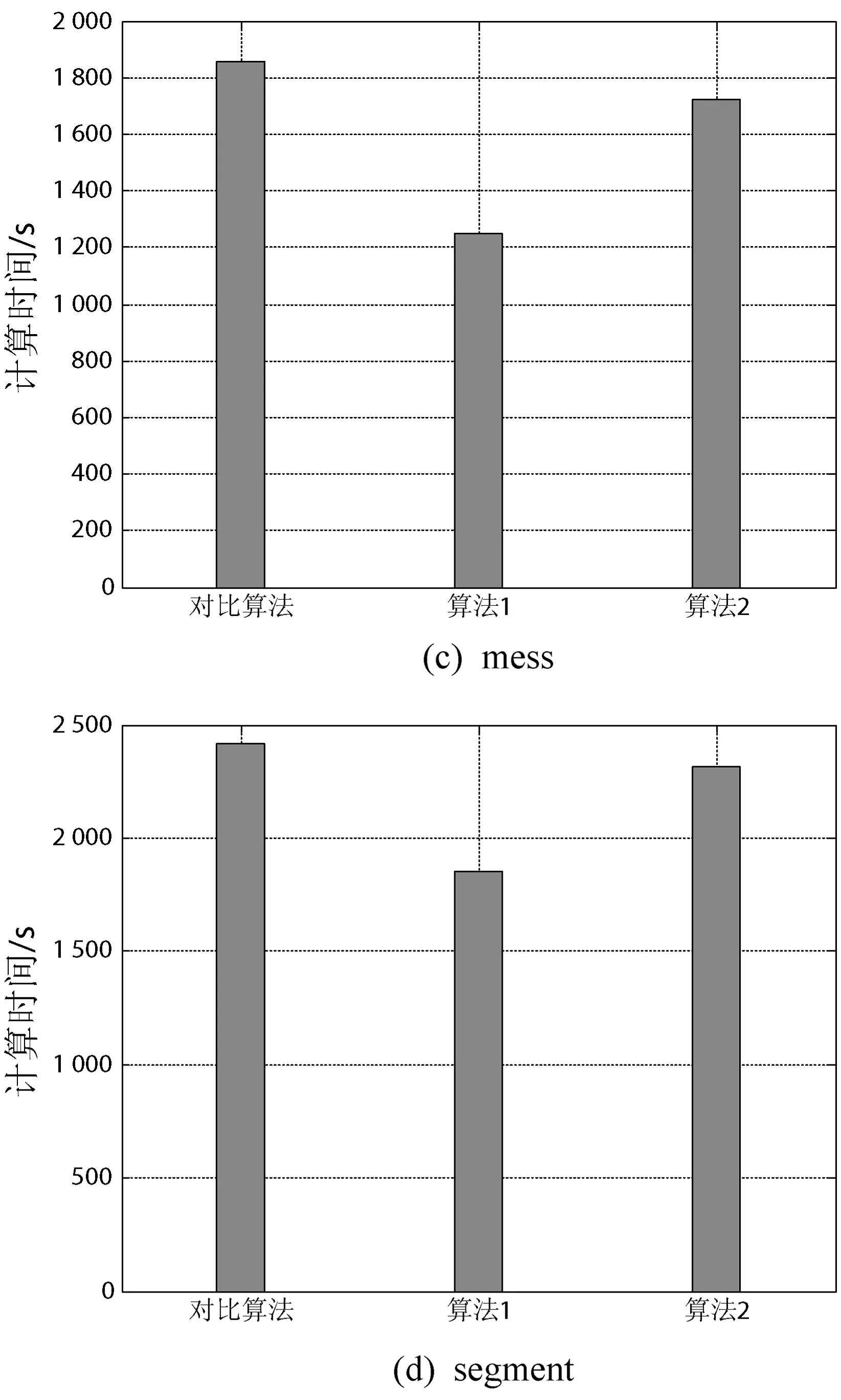
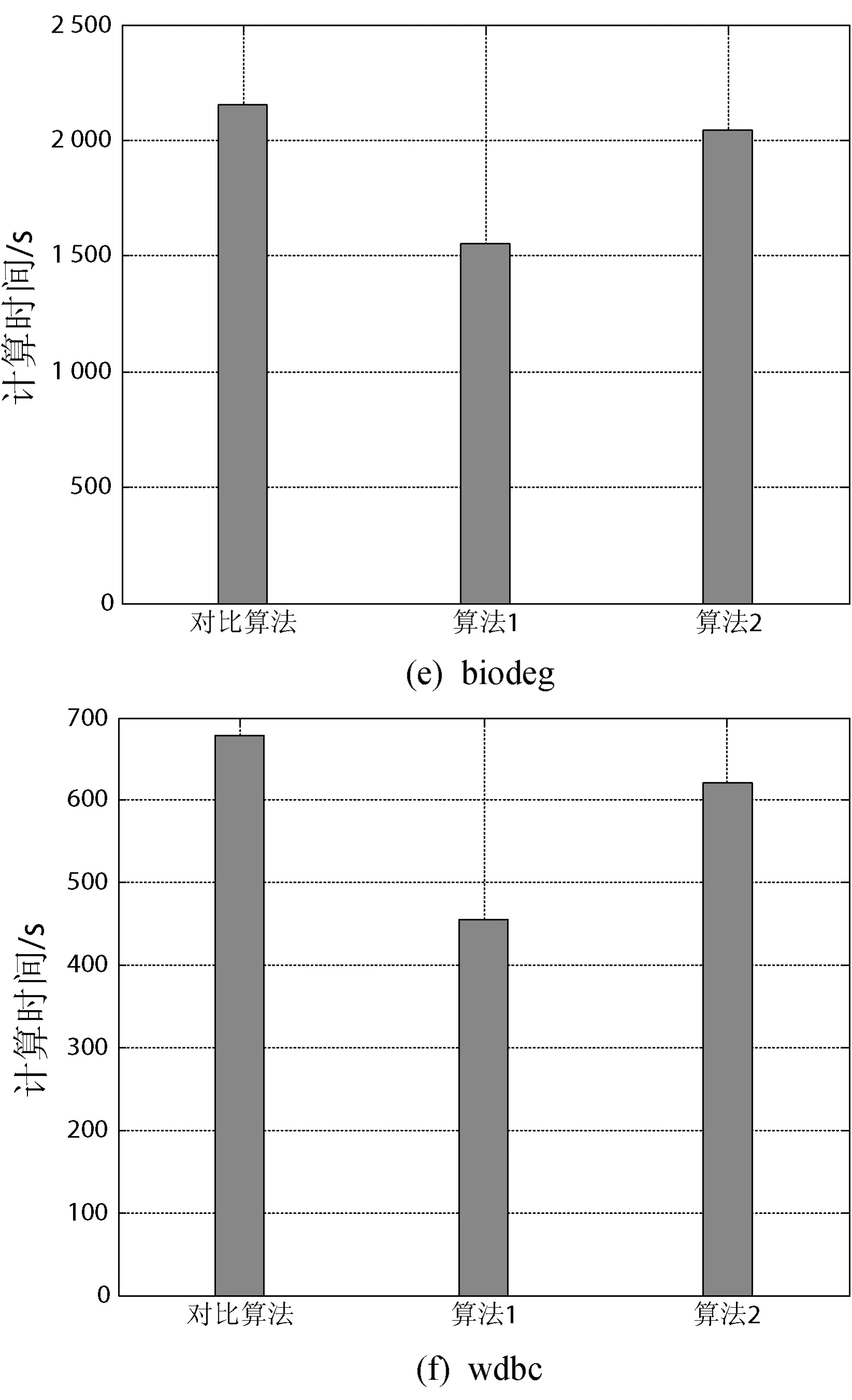
图2 算法效率比较

观察图2的实验结果，可以发现本文提出的算法1在多数数据集下有着较小的特征选择时间，这主要是由于算法1是基于增加策略来寻找特征约简集，当搜索完约简集后算法则终止。在这些数据集中，多数数据集的特征约简集都远小于特征全集，因此算法1的效率会更高一点。本文的算法2与对比算法的用时相差不大，这主要是由于在文献[15]中，对比算法也是一种基于删除策略来寻找特征子集的算法，因此与算法2有着相同的算法效率。

在特性选择算法中，特征约简集的分类精度也是评估特征选择算法性能的一个重要方面，实验将本文算法和对比算法得到的特征子集结果在支持向量机分类器(SVM)下进行分类性能评估，其结果通过分类精度的形式来表示，具体结果如表4所示。可以发现，两类特征选择算法得到分类精度均高于原始特征集的分类精度，同时本文算法1在大部分数据集下有着较高的分类精度，而算法2在数据集wine和wdbc下的分类精度较高，对比算法在各个数据集下的分类精度均小于算法1和算法2。因此本文提出的特征选择算法优于对比算法，同时本文的算法1相比算法2具有更高的优越性。

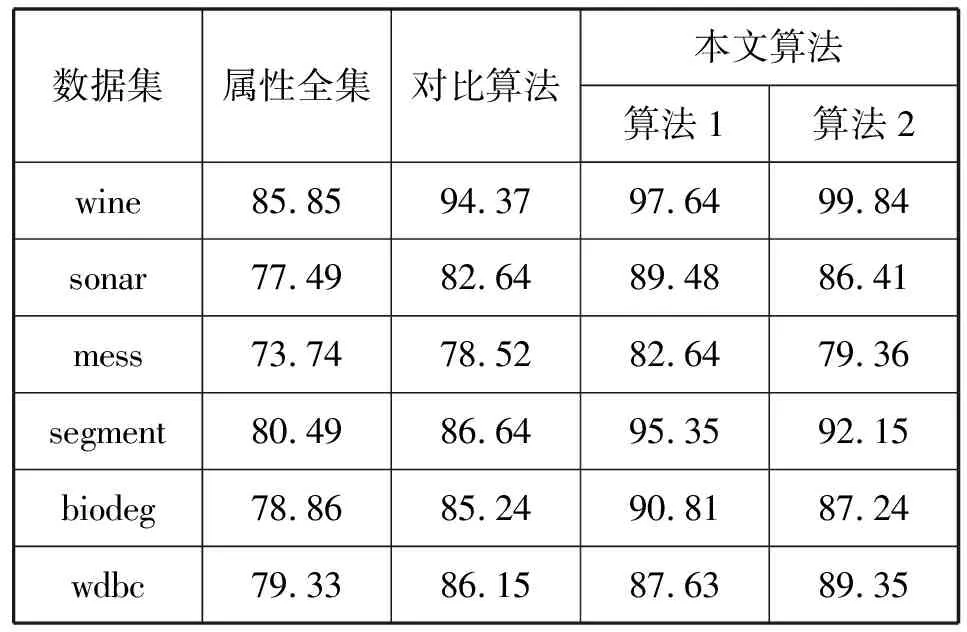
表4 分类精度比较 %

综合特征子集的决策代价结果、算法的效率和特征子集的分类精度，可以发现本文提出的改进模糊决策粗糙集最小化决策代价特征选择算法，比传统模糊决策粗糙集的特征选择算法具有更高的特征选择性能，同时本文提出的基于属性增加策略的最小化决策代价特征选择算法具有更高的优越性。

5 结 语

决策粗糙集模型是粗糙集理论的重要研究分支，在模糊集环境下，学者们提出了模糊决策粗糙集模型，扩大了决策粗糙集的适用范围。由于传统的模糊决策粗糙集对噪声数据不具有很好的容忍效果，本文通过在模糊相似关系上引入一个阈值的方式，提出一种改进模糊相似关系，进而构造出改进的模糊决策粗糙集模型。在该模型的基础上，基于不同的搜索策略，设计出了两种最小化决策代价特征选择算法，实验证明了算法的有效性，同时也间接证明了所提出模型的优越性。接下来将进一步探索所提出模糊决策粗糙集在实际中的应用。