基于DCIO-DNN和迁移学习的基因表达回归预测模型

薛艳锋 李 春 高永强

1(山西大学复杂系统研究所 山西 太原 030006) 2(吕梁学院计算机科学与技术系 山西 吕梁 033000) 3(太原理工大学信息与计算机学院 山西 太原 030024)

0 引 言

基因表达谱数据可被用于基因功能预测、作物优化、疾病相关基因发现和药物筛选等[1-4]，但获取过程繁杂、成本极高，难以开展大规模全基因组表达谱分析。人类基因组中包含约2万到2.5万个基因，利用表达之间的关联性，可确定调节因子和target基因构建基因调控网络[5]。由于大约有1 000个基因拥有80%CMap 数据的信息，所以测量这1 000个基因(命名为landmark基因)的表达谱可以预测剩余基因(命名为target基因)的表达[6]。文献[6]采用线性回归(LR)预测模型，虽然LR具有极高的泛化性能，但无法建模landmark和target基因之间固有的非线性关系[7]。核函数方法已被应用于非线性模型的构建中[8]，然而随着数据维度升高及数据增加，其泛化性能急剧下降。

深度神经网络可以建模非线性关系[9]。Peng等[10]在传统神经网络的基础上增加了输入层与输出层的直接连接建模了两者之间的线性和非线性映射关系。Pao等[11]在输入层与输出层之间增加随机向量可迭代获得最优解。

基于此，本文首先提出一种基于直连输入输出的深度神经网络和迁移学习的基因表达回归预测模型——直连输入输出的深度神经网络基因预测模型(Direct Connect Input and Output-Deep Neural Network Gene predict Model，DCIO-DNN_GM)，直连输入输出的具体含义为在经典神经网络的基础结构上，输入层与输出层之间有连边连接。该模型可同时建模landmark和target基因的线性和非线性映射关系，利用迁移学习和正则化技术在GTEx小数据集上训练模型，并验证和比较DCIO-DNN_GM模型的跨平台预测能力。最后以多指标、多角度分析不同模型的预测效果；结果表明：DCIO-DNN_GM模型的各项指标更高。

1 相关工作

1.1 深度神经网络

深度神经网络(DNN)的层与层之间是全连接的，第k层第j个神经元的计算公式为：

(1)

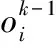
1.2 迁移学习策略

迁移学习[12-13]的思想是为任务A开发的模型MA被重用为任务B模型的起点，具体在深度学习中，固定模型MA前面部分权重或参数再利用任务B的数据继续训练，其核心是找到任务A与B的相似性或某种映射关系[14]。

2 模型设计

2.1 基因表达谱数据预处理

Gene Expression Omnibus(GEO)数据集[15]和Genotype-Tissue Expression(GTEx)数据集[16]来自不同的平台，如表1所示，且两平台测量的单位及量纲不同，因此调用Python库Sklearn[17]的MinMaxScaler方法进行数据归一化预处理，进而达到相同的表达水平。

表1 数据集信息

2.2 基因表达回归模型构建

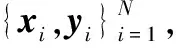
传统的DNN网络模型包括输入层、输出层和若干隐藏层，其中输入层的节点取决于数据的特征个数，输出层的节点取决于问题本身，隐藏层通过调整权重实现特征数据到标签数据的逼近。本文提出的DCIO-DNN_GM模型，如图1所示。其输出层的结果不但经过了隐藏层的非线性映射，而且融入了输入层的线性组合。所以DCIO-DNN_GM可以建模输入数据与输出数据的线性和非线性映射。

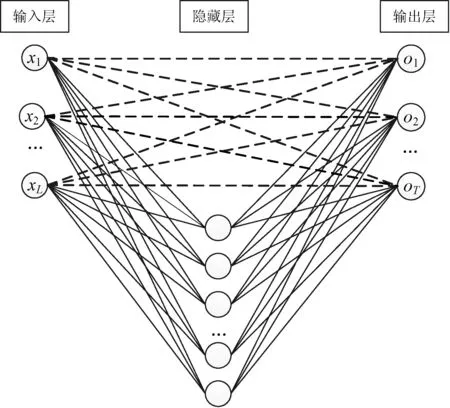
图1 DCIO-DNN_GM的网络结构

DCIO-DNN_GM模型的学习过程为隐含层的输出C和输出层的输出O：

C=f(∑W1X+α)

(2)

O=∑W3X+∑W2C+γ

(3)

式中：f表示隐藏层的双曲正切激活函数；W1表示隐藏层与输入层的权重；X表示输入数据；α表示隐藏层的偏置向量；W3表示输入层与输出层权重(图1中虚线部分)；W2表示输出层与隐藏层权重；γ表示输出层的偏置向量。

3 实 验

3.1 实验环境与误差衡量

本文所有实验都采用损失函数为均方误差(MSE)，性能指标包括平均绝对值误差(MAE)、归一化均方根误差(NRMSE)以及决定系数(R2)，计算公式分别如下：

(4)

(5)

(6)

(7)

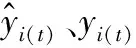
3.2 实验结果与分析

本文实验分别对应线性模型(LR)、传统深度神经网络模型(D-GM)、本文模型(DCIO-DNN_GM)在误差性能、跨平台预测能力和拟合效果三方面的对比分析。

实验一：对比LR、D-GM和DCIO-DNN_GM在GEO数据上的MAE和NRMSE，结果如表2所示。本文模型不同参数组在GEO验证集的误差如表3所示。

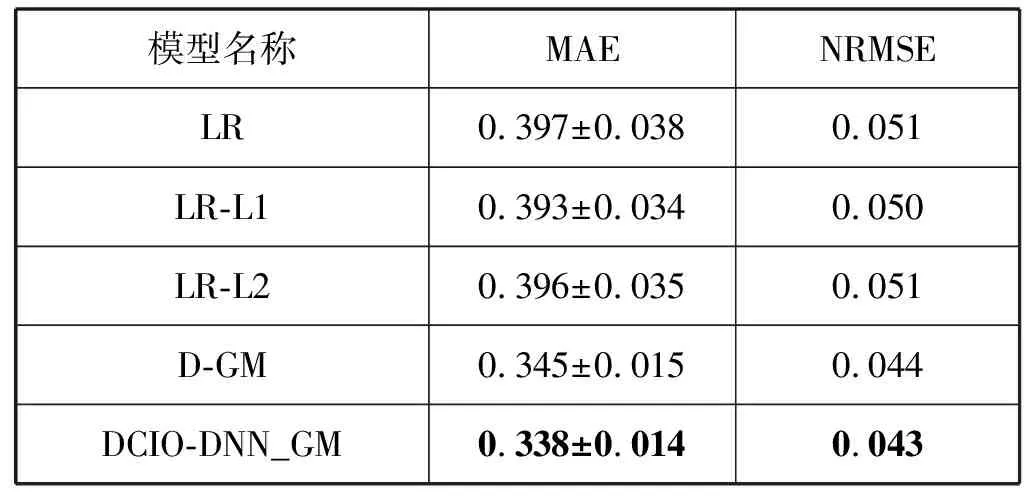
表2 不同回归模型在GEO验证集的误差

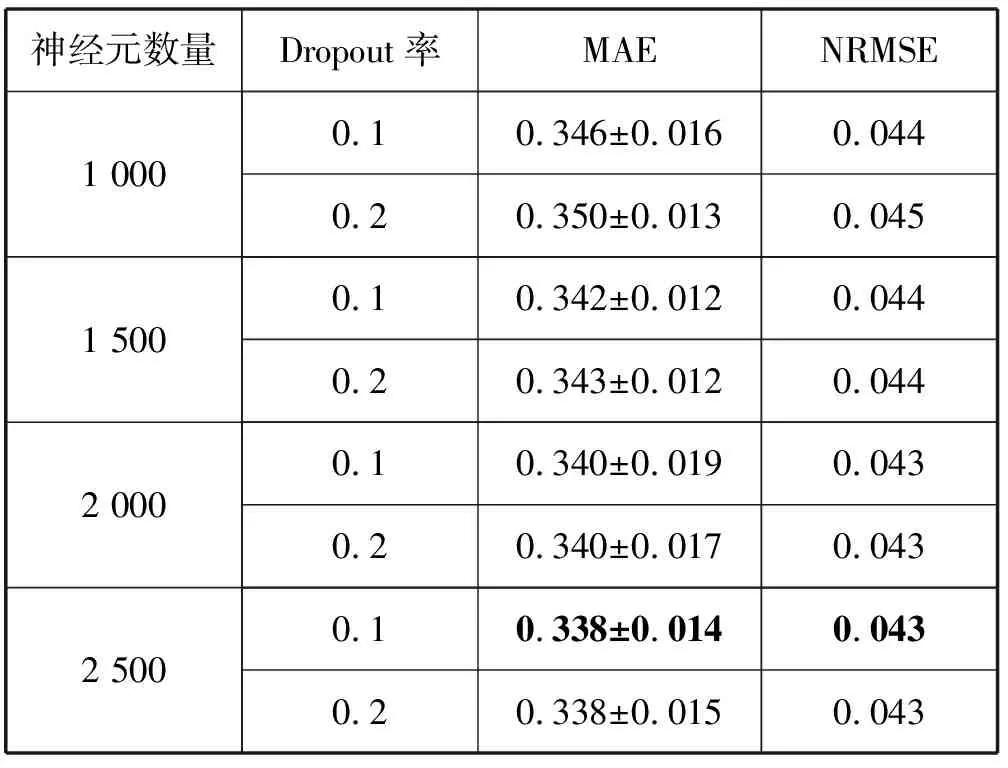
表3 DCIO-DNN_GM模型不同参数组在GEO验证集的误差

“±”后的值是所有target基因MAE的标准偏差。如表2所示，LR模型分别采用L1和L2正则化技术，D-GM和DCIO-DNN_GM模型采用Dropout技术且参数配置相同(只包含一层隐藏层)。如表3所示，依据MAE和NRMSE最小的原则，选择神经元数量与Dropout率的最优组合进行后续比较分析，结果如表4所示。

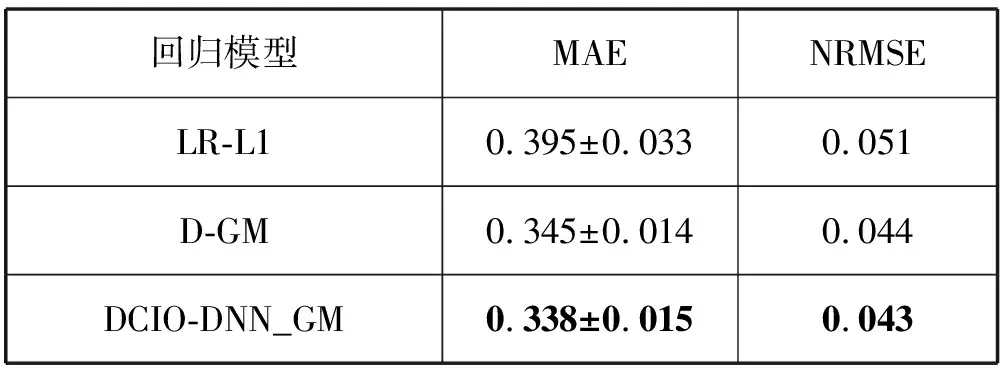
表4 不同回归预测模型在GEO测试集上的实验误差

由表4可知，相比于LR-L1和D-GM，DCIO-DNN_GM在两个指标上都有所降低，提升了误差性能。

实验二：采用迁移学习方法解决GTEx数据集小样本(如表1所示)无法直接训练模型的难题。

表5给出了不同模型在GTEx测试集上的实验结果，其中LR-L1模型仅使用GTEx数据拟合，D-GM和DCIO-DNN_GM模型使用迁移学习技术。具体方法为：首先将GTEx数据分成GTEx训练集和GTEx测试集，在实验一的基础上结合迁移学习的微调策略，将D-GM和DCIO-DNN_GM模型隐藏层的前两层权重参数固定，然后使用GTEx训练集数据训练D-GM和DCIO-DNN_GM模型，最后使用GTEx测试集数据检验不同模型在GTEx数据集上的预测能力。相比于LR-L1和D-GM，DCIO-DNN_GM在MAE指标上有所降低，提升了跨平台预测能力。

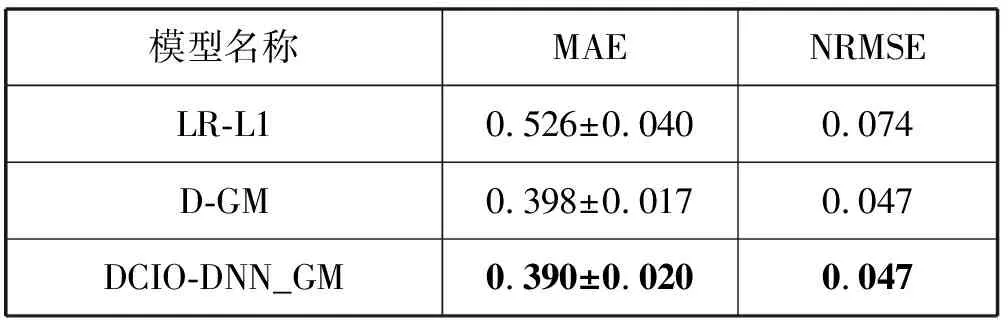
表5 不同模型在GTEx测试集数据上的实验误差

综上，本文提出的DCIO-DNN_GM模型误差更小，可迁移性更高，通过5组GEO测试集中target基因表达值的真实值和预测值的箱线图对比(如图2所示)，证明了DCIO-DNN_GM模型可以预测target基因表达值。

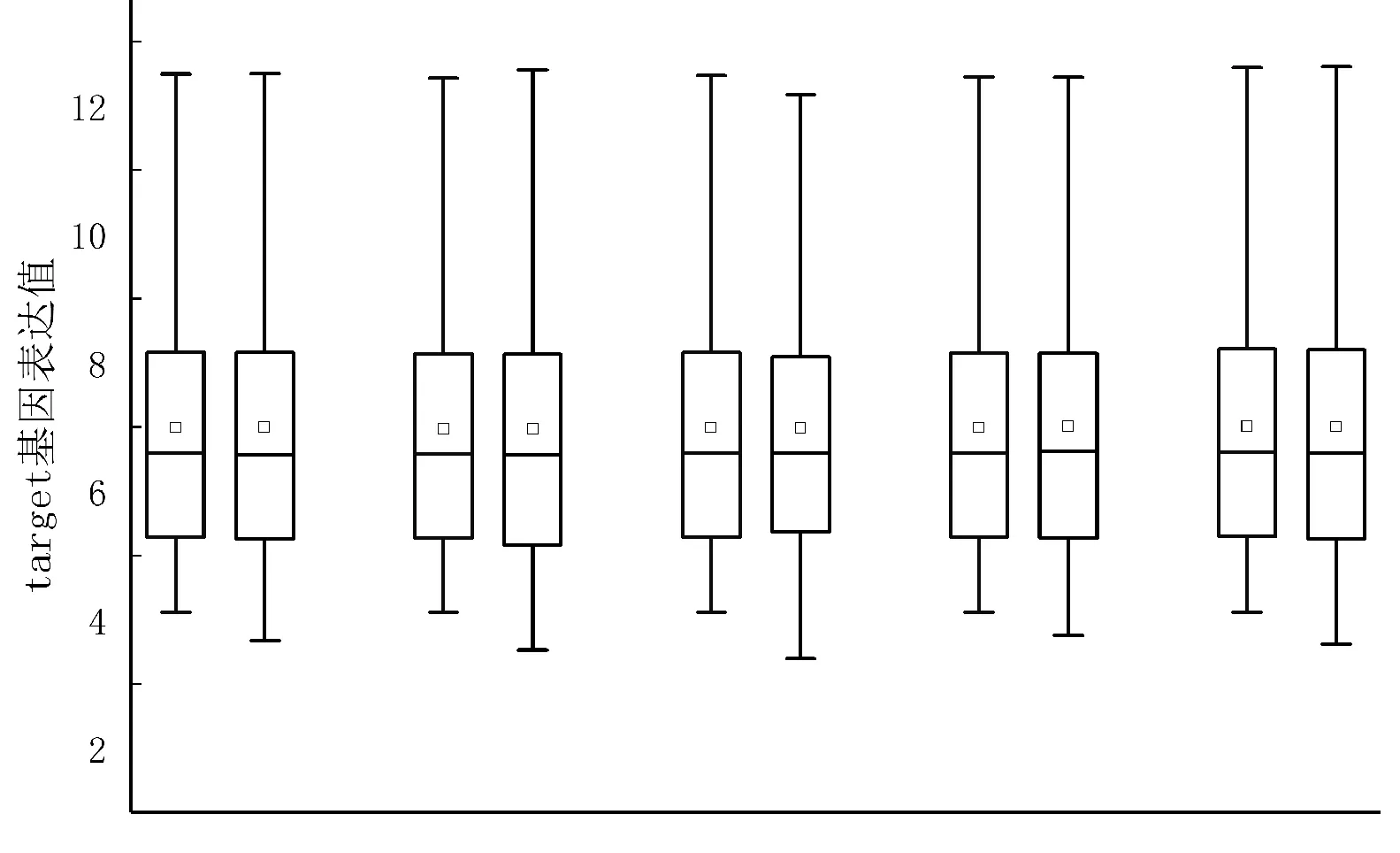
图2 target基因真实表达值与预测表达值对比箱线图

实验三：使用决定系数(R2)比较LR-L1、D-GM和DCIO-DNN_GM模型的拟合能力。

表6给出了三种回归模型预测9 520个探针的target基因R2分布情况。由表6可知，在[0.8,1.0)区间内，DCIO-DNN_GM模型分别是LR-L1和D-GM模型的1.92倍和1.74倍。在[0,0.6) 区间内，LR-L1和D-GM模型分别是DCIO-DNN_GM模型的1.57倍和1.49倍。结果证明DCIO-DNN_GM拟合效果更好。

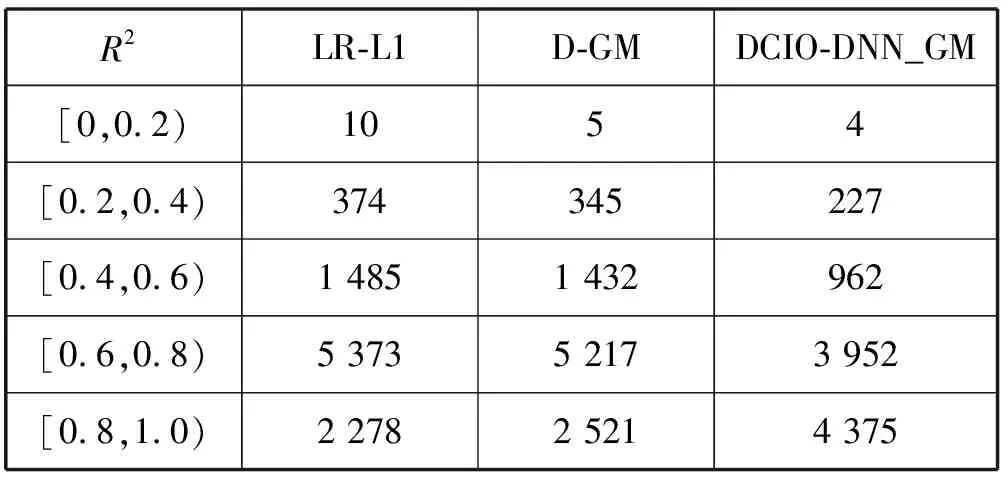
表6 决定系数R2分布情况

4 结 语

针对基因表达谱数据高维度、少样本和非线性的现实问题，本文提出DCIO-DNN模型并获得更低的MAE和NRMSE，然后提出DCIO-DNN_GM解决了GTEx数据集小样本无法训练的问题。再通过箱线图比较了该模型可以预测target基因表达值，最后通过R2分布区间说明该模型的拟合数据能力更强。

然而该模型是数据驱动建模，整个过程都是利用深度神经网络拟合数据的能力而未考虑基因表达本身的机理，结合基因表达本身的机理与神经网络拟合数据的能力建模是未来研究的方向。