基于响应时间的混合关键级系统弱约束调度策略研究
金永贤 胡心洁
(浙江师范大学数学与计算机科学学院 浙江 金华 321004)
0 引 言
在传统实时系统执行过程中,所有任务的响应时间小于其截止期限可以保证系统的顺利运行。其中响应时间可通过Joseph等[1]提出的方法进行计算。然而现如今的实时系统日益呈现功能多样性、计算密集性、时效敏感性的特点,相应的物理平台越来越小,因此传统的实时系统不再适用,要求不同重要性的任务共享同一个平台,混合关键级系统应运而生。与传统的实时系统不同,混合关键级系统的任务根据重要性分为不同的关键等级,外部环境的变化会引起系统关键等级的变化,对应的任务执行模式也会发生变化,从而影响任务的可调度性。因此传统实时系统的任务可调度算法不再适用于混合关键级系统,Vestal[2]首先建立混合关键级系统模型,提出响应时间计算方法,并结合Audsley[3]提出的OPA算法对任务进行优先级分配。
研究人员在文献[2]模型的基础上进行研究,系统多以任务的最坏情况执行时间(WCET)作为关键参数(关键参数是任务参数中因系统关键级改变而变化的参数),且保证高关键级任务的正确执行,通常需要牺牲低关键级任务的执行时间。但在实际应用中,简单地丢弃低关键级任务可能造成资源的浪费以及数据完整性的破坏[4],且频繁地丢弃任务也会增加开销。对此,研究人员开始研究积极调度低关键级任务的方法:在关键级提升时,不采用简单地丢弃低关键级任务的方法,而将其以较低的服务水平执行,从而保证系统稳定执行,提高资源利用率。
Gettings等[5]在双关键级任务模型下提出积极调度低关键级任务的方法:在系统进入高关键级阶段后,低关键级任务以弱约束的模式继续执行,即允许低关键级任务连续几个工作业不执行,并提出两个调度策略,这两个调度策略有一定局限性,在实际应用中任务关键级通常多于2个,如:适用于商用飞行器的RTCA DO.178B航空电子软件标准将任务划分为成5个安全保证等级;ISO26262将任务划分为4个安全等级。对此本文建立混合多关键级模型,改进弱约束模式,并基于响应时间分析提出调度策略。
1 相关研究
针对经典的混合关键级模型,研究人员已基于响应时间计算提出了几种调度策略。Baruah等[6]在Vestal基础上进行进一步研究,以混合双关键级系统为模型提出了SMC、AMC调度策略。文献[7]将AMC调度策略扩展到多关键级系统;文献[8]以悲观周期作为关键参数,基于响应时间分析提出调度算法;文献[9]提出一种新的计算响应时间的方法,关注系统提升时任务自身的执行时间,降低了响应时间计算的复杂度。Burns等[10]进一步改进混合关键系统模型,加入可容错的概念,保证系统鲁棒性和可调度性之间的平衡。
在低关键级任务积极调度的研究方面,赵瑞姣等[11]针对异构多处理器调度中存在的问题,引入回收队列重新调度被丢弃的任务,从而提高低关键级任务的调度比率。Bernat等[12]提出弱实时系统的概念,允许任务在某几个释放周期错过截止期限。文献[5]将弱实时系统的概念引入到混合关键系统中,实现低关键级任务的弱约束模式执行。此外,许多研究人员引入弹性模型对低关键级任务进行积极调度,其中Su等[13]使用提前释放策略,将高关键级任务执行时产生的空闲时隙分配给低关键级任务执行,低关键级任务释放周期可以弹性调整,选择合适的空闲时隙执行。文献[14]将该算法进行改进使其适用于多处理器平台。黄丽达等[15]也使用了弹性调度模型的调度算法,积极地调度低关键级任务。文献[16]根据系统负载的变化,实现任务周期的动态延伸或压缩,从而保证更多任务执行,提高了处理器利用率。Ren等[17]将任务进行分组,高关键级任务只能影响与其同组的低关键级任务的执行,从而提升低关键级任务的可调度性。文献[18]引入重要性概念,对低关键级任务进行重要性分配,低关键级任务按照其重要性的逆序被丢弃。Chen等[19]提出一种灵活的混合关键级模型,在关键级提升时,只有溢出任务本身被认为表现出高关键级行为,而其他高关键级任务仍然保持以前相同的模式执行,能够在保证系统可调度的同时确定低关键性任务的最大可执行时间。
2 任务模型及相关概念
2.1 任务模型
首先建立混合多关键级系统的任务模型:在单处理器可抢占平台上,包含N个独立任务的任务集τ(τ1,τ2,…,τn)等待运行,且不同关键级的任务共享一个平台。下面定义任务参数和执行模式。
用系统参数L={L1,L2,…,Lm}表示系统当前关键等级,L1为系统的初始关键等级,Lm为系统可达到的最高关键等级。
任务参数可描述任务执行模式。每个任务τi有6个参数(Ci,Ti,Di,Li,(m,sLi(L)),pi),Ti为任务周期,Di为隐含式截止期限(Di=Ti),pi代表任务的优先级,Li为任务关键等级,任务最坏情况响应时间向量Ci=(Ci(L1),Ci(L2),…,Ci(Ln)),参数(m,sLi(L))规定任务的弱约束执行模式。
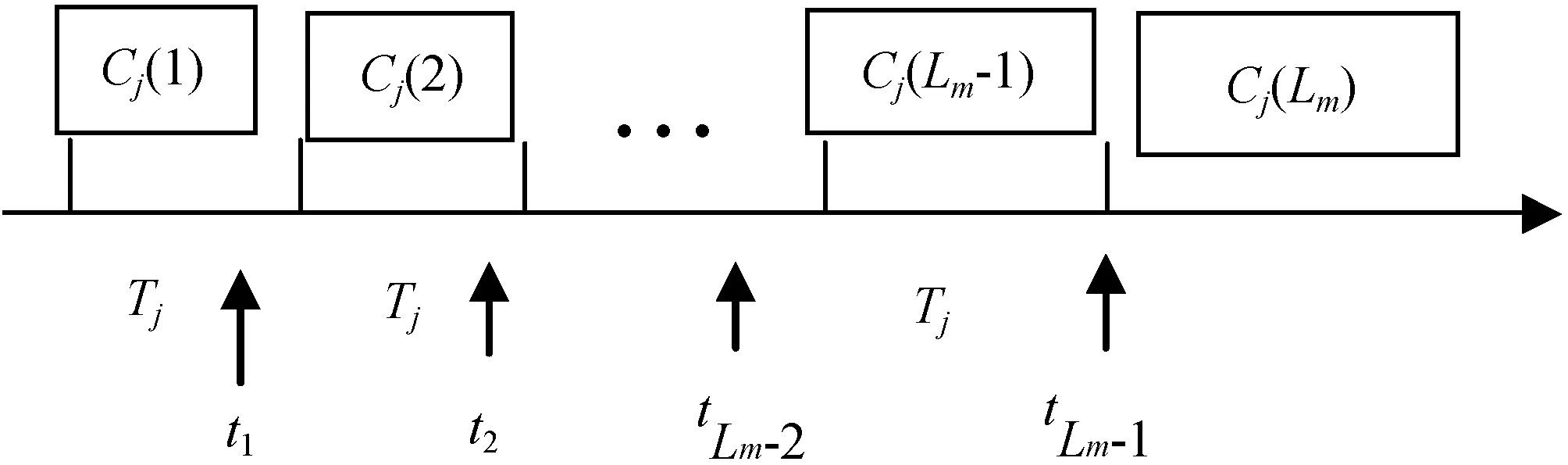
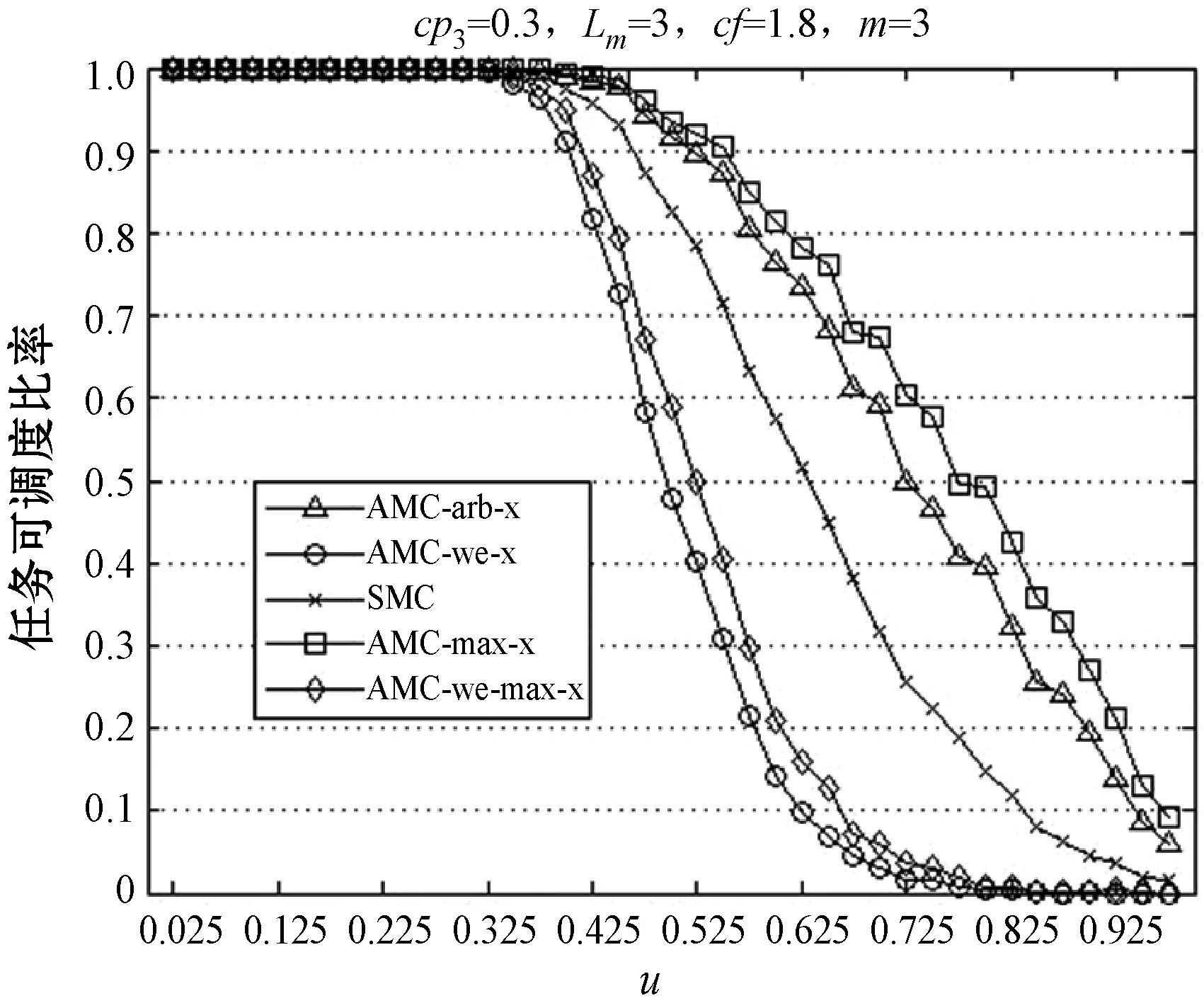
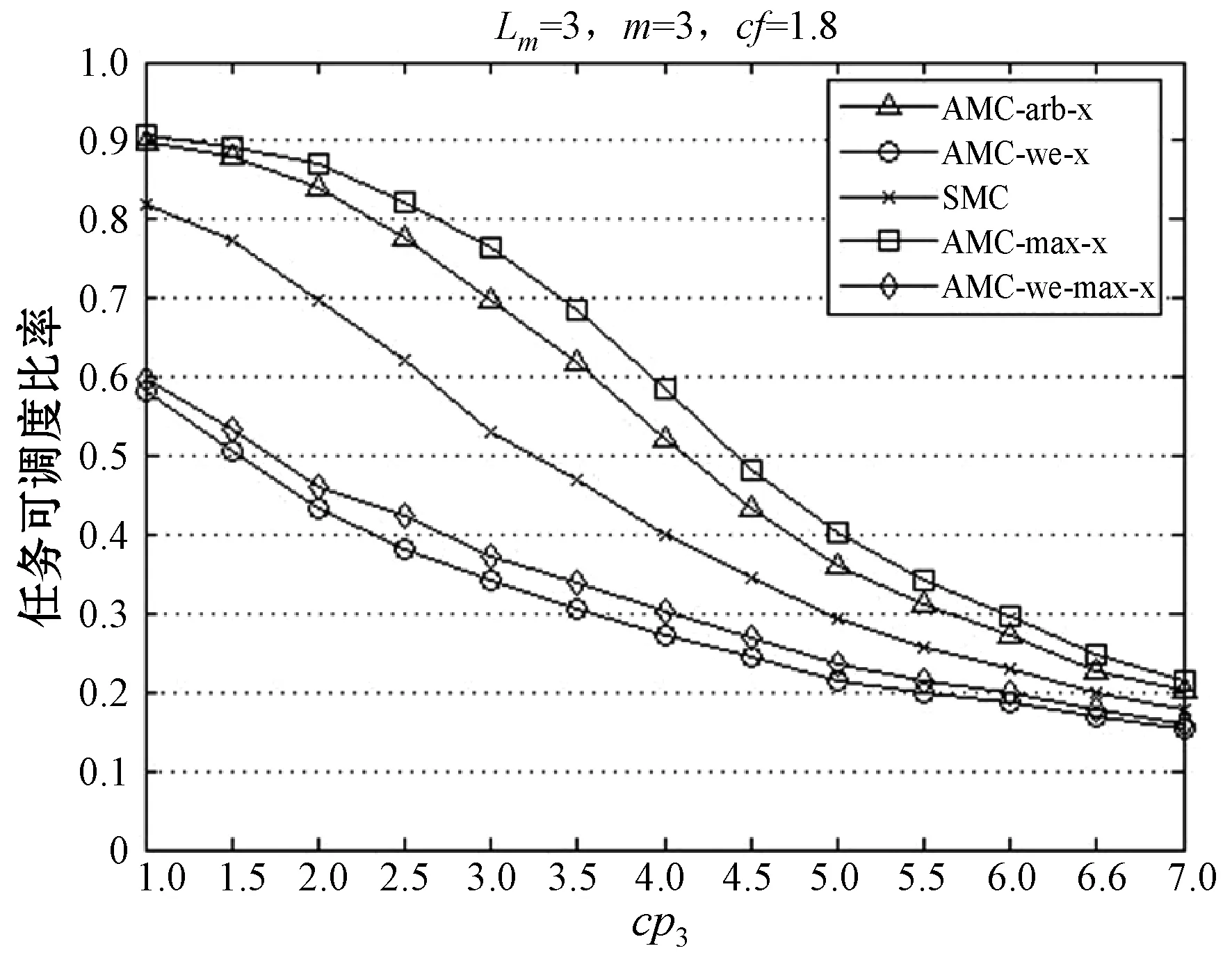
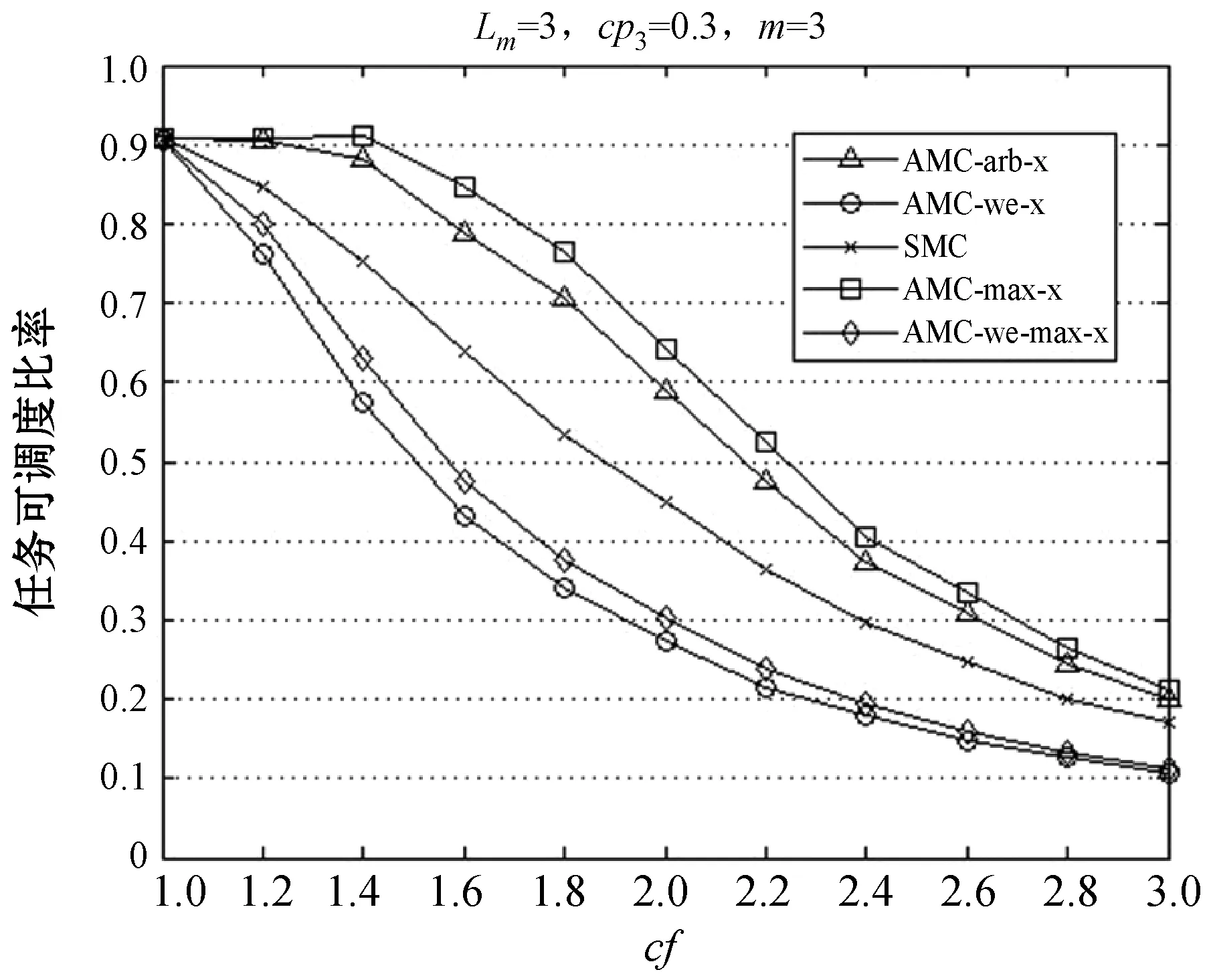
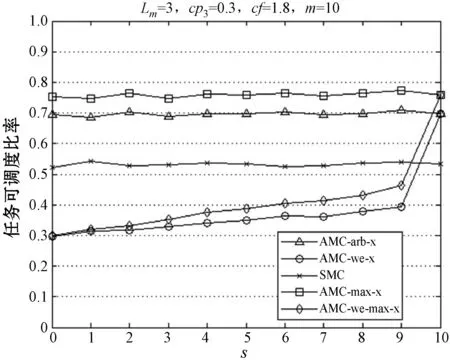
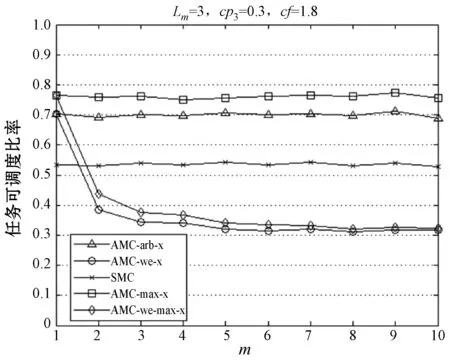
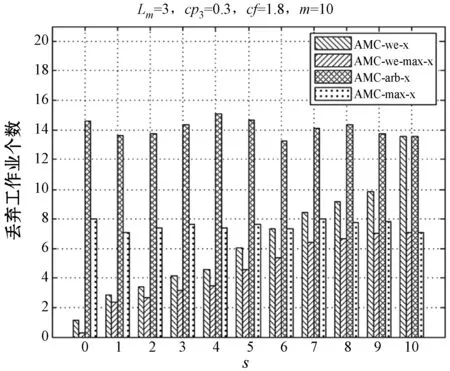
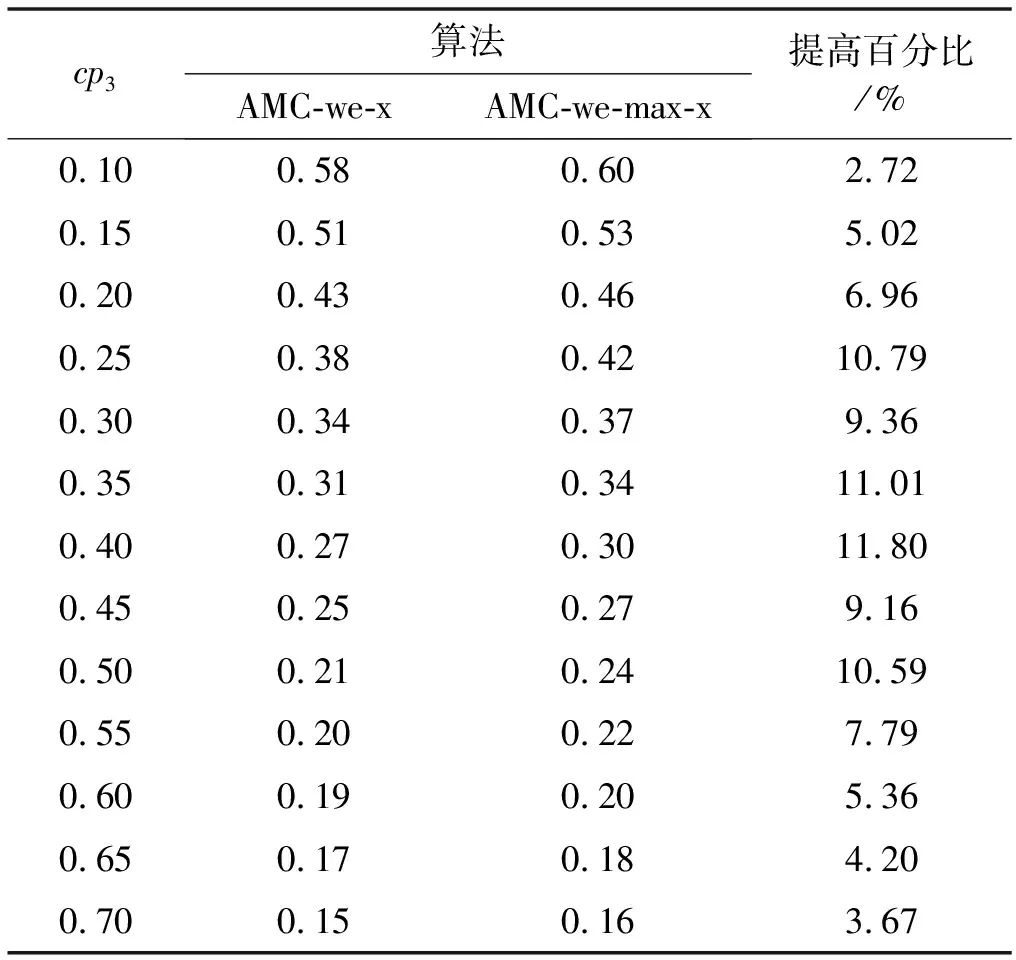
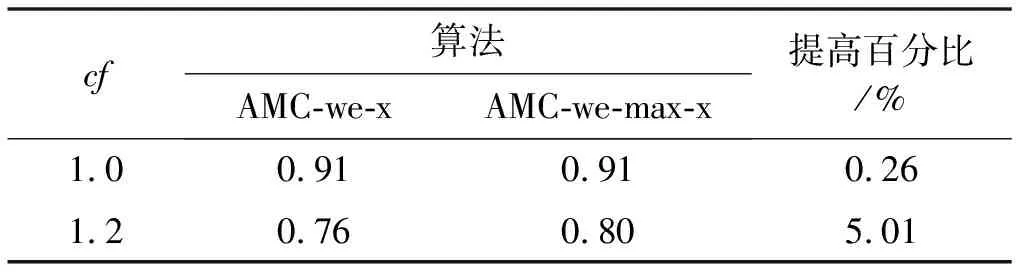
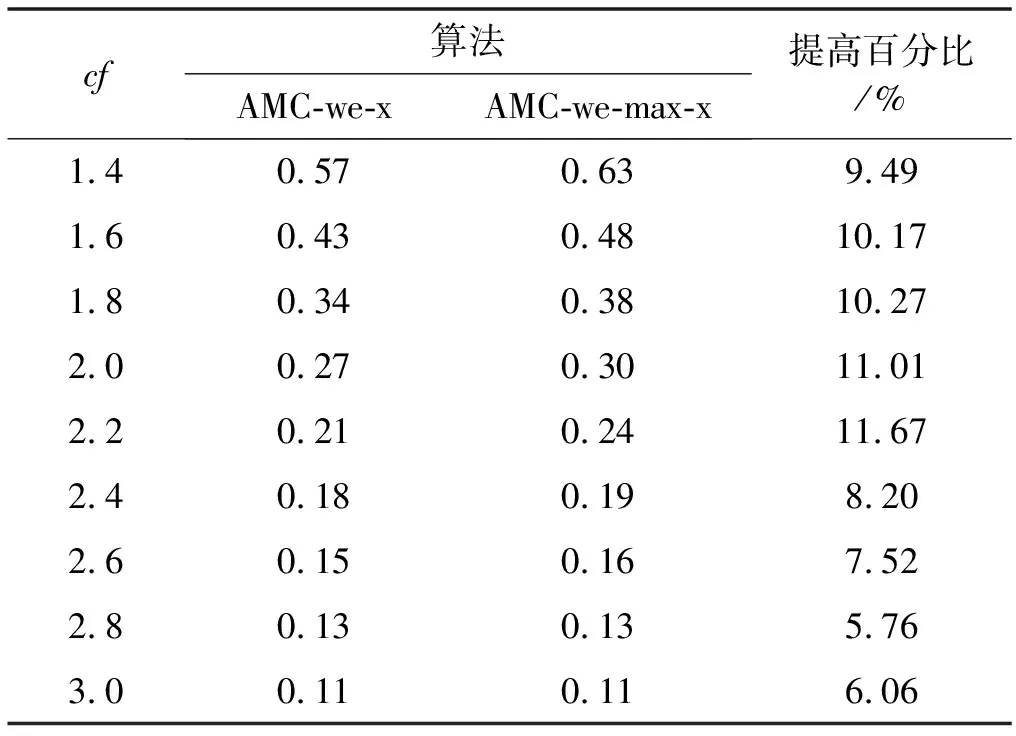
任务的执行模式。任务的最坏情况执行时间在系统处于不同关键等级时有以下关系:当L 响应时间:本文在线下对任务的工作业从释放到执行完毕经历的总时间做出估计,这个值为任务的响应时间。 任务执行窗口:已知τi首个工作业在0时刻释放,响应时间为Ri,(0,Ri)即为τi的执行窗口。 任务可调度:若任务τi可被分配合适的优先级,则判定τi为可调度。 可调度任务集:若所有τi∈τ都可被分配到合适的优先级,则该任务集称为可调度任务集。 τ为待分配优先级的任务集。结合OPA算法[3]对τ中的每个任务进行优先级分配,以此判断任务集的可调度性,如算法1所示。 算法1WE-OPA 输入:任务集τ。 输出:任务集τ的优先顺序集P。 functionFLAG(τ) fork=N→1do flag←false fori=1→length(τi)do pi←ki flag←true τi←[] break end if end for if flag=flase then return failure end if end for return success end function 任务模型基于可抢占处理器平台,因此任务执行时会受到高优先级任务的抢占而产生干扰时间。由算法1可知,τi在待分配任务集中处于最低优先级,除τi外的其他任务为干扰任务,生成一个集合hp(i)。现判断τi是否可调度,根据文献[20],任务总响应时间为本身执行时间与hp(i)中的任务产生的干扰时间的总和,而本文为区分任务的关键级别,hp(i)集合又以系统当前关键等级L为界限分成两个子集,对应的干扰时间表示为ILj Ri(l)=Ci(l)+ILj (1) 干扰任务τj∈hp(i)在τi的执行窗口内以固定周期Tj释放多个工作业。传统实时系统的干扰时间[20]: (2) 首先求出干扰任务τj在τi执行窗口内释放的工作业总数(Ri(l))/Tj,与任务i的最坏情况执行时间相乘,类似地得出干扰时间总和。本文在该公式的基础上进行演变,分析系统在不同执行模式下的干扰时间。 系统运行时需经历稳定运行和关键等级切换两个阶段,干扰任务在这两个阶段对τi产生的干扰时间也不一致。因此τi的响应时间分为两部分:静态部分和关键级切换部分。 4.2.1静态部分 假设当前系统稳定在关键等级k运行,干扰任务在τi的执行窗口内有稳定的执行模式,对于每个τj∈hp(i),可在整个执行窗口内确定实际执行的工作业个数,修改式(2)为: (3) 4.2.2关键级切换部分 干扰任务的最坏情况执行时间和实际执行工作业数量随着系统关键等级动态变化。假设系统关键等级已提升至L,可对执行窗口进行划分,以关键等级提升经历的时间段作为一个子窗口,如系统关键等级从k提升至k+1对应的子窗口为(Ri(k),Ri(k+1)),Ri(k)是系统关键等级在k稳定运行时τi的静态响应时间。分别计算每个子窗口的干扰时间,并求出总干扰时间: (4) 特别地,ε取值为L-1时,对应的子窗口为(Ri(L-1),Ri(L)),Ri(L)作为响应时间值参与迭代计算。 比较的调度策略有SMC、AMC-arb-x以及AMC-max-x。SMC由Baruah等[6]提出,规定所有任务执行时间不超过自身关键级对应的Ci(Li),只在静态条件下分析响应时间,而AMC进一步地考虑关键级的提升对响应时间的影响,Li等[21]在Fleming等[7]的基础上完善了混合多关键级系统的调度策略:包括SMC和AMC-arb-x和AMC-max-x。 现有的弱约束执行模式只适用于双关键系系统,且规定任务的几个工作业必须连续“跳过”执行[5],而本文的执行模式消除了这个限制,并扩展至多关键级系统。假设系统当前关键等级为L,对于所有τi∈τ,Li 调度策略AMCwe-x和AMCwemax-x响应时间计算重点有两个方面:(1) 根据弱约束模式的分配规则计算干扰任务在执行窗口内实际执行的工作业数量;(2) 确定干扰任务不同工作业的最坏情况执行时间。区别在于两个调度策略对子窗口的划分方式不同,且干扰任务工作业的最坏情况执行时间有不同的变化趋势。 关键等级提升至L需经历L-1次提升阶段,AMC-we-x调度策略没有精准确定系统关键等级提升的时间点,将干扰任务在τi的整个执行窗口(0,Ri(L))释放的工作业的最坏情况执行时间都估计为Cj(L),而忽略系统关键级提升过程中Cj值的变化。AMC-we-max-x策略设定L-1个提升的时间点,并以提升点调整子窗口,每个子窗口内释放的工作业最坏情况有不同的估值。因此AMC-we-x策略悲观估计了干扰任务工作业的最坏情况执行时间,在响应时间计算的精确方面低于AMC-we-max-x,但AMC-we-max-x调度策略需枚举所有提升序列对应的响应时间,算法复杂程度较高。 假设在系统关键等级为L时对任务进行调度,由分配算法可知需计算τi响应时间以判断该任务是否可调度。 4.6.1静态部分响应时间 系统需经历L个稳定运行阶段。现讨论系统稳定在关键等级k(k∈(1,L-1))时任务的响应时间。可根据弱约束执行模式计算两部分干扰时间,从而求得响应时间Ri(k),过程如下: 1)ILj (5) 第一部分为τi执行窗口(0,Ri(k))内τj释放的工作业总数,第二部分为应“跳过”的工作业个数。 2)Lj≥k的干扰任务在τi的执行窗口内以正常模式执行,即sLj(k)=0,τj释放的总工作业即为实际执行的工作业: (6) 另一方面,干扰任务τj在τi执行窗口内有固定的最坏情况执行时间Ci(k),Lj Cj(Lj) (7) (8) 将式(7)和式(8)代入式(1),可求出静态部分总响应时间: Cj(Lj) (9) 4.6.2关键级切换部分响应时间计算 1)ILj≥l(l)部分,干扰任务τj在整个执行窗口内没有工作业丢失,且τj所有工作业的最坏情况执行时间为Cj(L),干扰时间计算如下: (10) 2)ILj (11) τj在τi的执行窗口内应跳过的工作业总数如下: (12) 由此可得出总响应时间为: (13) 若待分配任务τi的关键等级小于L,由于具体的关键级提升点未知,可假设任务τi首个工作业没有被丢弃,且干扰任务在τi窗口内没有工作业跳过。响应时间为: (14) 现确定关键级提升的时间点,从k提升至k+1的提升点tk在(Ri(k-1),Ri(k))之间,τj在tk前释放的工作业最坏情况执行时间仍为k-1关键等级对应的Cj(k-1),tk后释放的工作业最坏情况执行时间为Ci(k)。如图1所示,以提升点为分界调整子窗口,将(tk,tk+1)作为系统关键等级处于k+1阶段的子窗口。 图1 调整任务子窗口 1) 计算ILj (15) 已知系统关键等级k (16) 2)ILj≥l部分的干扰时间如下: (17) 干扰任务在(tk,tk+1)子窗口对应的最坏情况执行时间为Cj(k+1)。 综上,得到总响应时间计算公式: (18) 实验参数:任务集包含的任务数量N,任务周期Ti:在10 ns~1 s范围内按均匀分布生成。任务集利用率u采用UUnifast算法生成[22],可以通过任务集总利用率和任务个数生成每个任务的利用率。系统最大关键等级Lm。任务执行时间Ci(L):L1关键等级下τi的最坏情况执行时间Ci(L)=u×T。不同关键级的最坏情况执行时间有如下关系:Ci(L+1)=cf×Ci(L)。cf为Ci的关键级扩展参数。不同关键级的任务所占比率cp=(cp0,cp1,…,cpm)。cpk代表关键级为k的任务所占比率。弱约束执行模式参数(m,sLi(L))。 通过六组实验对比相同任务集在AMC-arb-x、AMC-max-x、SMC、AMC-we-x、AMC-we-max-x 5个调度策略下估计所得的可调度比率以及低关键级任务丢弃比率。 除实验四和实验六外,弱约束模式中的参数值取为s2(3)=s1(2)=1,s1(3)=2,N取固定值20,可调度比率f(p)=可调度任务集个数/总任务集个数。 实验一分析利用率变化对任务集可调度比率的影响,u在(0.025,0.975)之间变化,步长为0.025,每个利用率下生成1 000个任务集,结果如图2所示。 图2 任务可调度比率随u变化曲线 实验二至实验五分析cp、cf、弱约束模式参数变化与可调度比率的关系,使用加权可调度比率公式[20]: (19) 式中:Wy(p)代表参数p下由算法y计算得到的加权任务可调度比率;sy(τ,p)表示任务τ集在参数p下用算法y计算得到的可调度比率;u(τ)表示总利用率,在每个参数p下计算在利用率(0.025,0.975)之间任务的可调度比率,且每个利用率生成100个任务集。 实验二观察cp值变化对任务可调度比率的影响,如图3所示。 图3 任务可调度比率随cp3变化曲线 实验三观察cf变化时任务可调度比率的变化趋势,如图4所示。 图4 任务可调度比率随cf变化曲线 实验四通过改变参数s,观测任务集可调度比率的变化趋势,如图5所示。 图5 任务可调度比率随s变化曲线 实验五通过改变参数m,观测任务集可调度比率的变化趋势,如图6所示。 图6 任务可调度比率随m变化曲线 实验六通过改变参数s,研究Li<3的任务丢弃比率变化趋势,如图7所示。 图7 丢弃工作业数量随s变化曲线 可得出以下结论:在所有调度策略下任务集的可调度比率随着u、cf、cp的增加而下降,AMC-we-max-x以及AMC-max-x的整体调度性能分别优于AMC-we-x以及AMC-arb-x。 表1和表2分别为AMC-we-max-x提升比率随cp3和cf的变化情况。可以看出,当Li=3的任务所占比例为0.1时,AMC-we-x与AMC-we-max-x的任务可调度比率接近,随着cp3的增大两者差距呈现增长趋势,说明AMC-we-max-x策略对有较多高关键级任务的任务集的调度有明显优势。cp值在0.4左右时提升效果最明显。同样地,当cf取值2.2左右时,AMC-we-max-x任务可调度优势比较明显。 表1 AMC-we-max-x提升比率随cp3变化情况 表2 AMC-we-max-x提升比率随cf变化情况 续表2 对比实验四到实验六数据,分析弱约束执行模式参数的变化对任务可调度比率的影响,当m=sLi(L)时,AMC-we-x与AMC-we-max-x的执行模式与AMC-arb-x与AMC-max相同,因此任务可调度比率也一致(见图5-图6)。当固定sLi(L)值,改变m,因为随着m增加,Li<3任务工作业的丢弃比率减少,导致整体调度比率下降;同理,随着s增加,Li<3任务丢弃的工作业增加(见图7),整体调度比率随之增加。 本文建立了一种新的混合多关键级任务模型,并基于响应时间分析提出两种调度策略,在系统未实际运行前对任务集进行优先级分配,并在悲观条件下分析可调度比率。修改了原有的弱约束执行模式并扩展至多关键级,给任务在不同系统关键级下设置对应的弱约束执行模式参数,通过实验得出结论:由于AMC-we-x和AMC-we-max-x没有简单地丢弃所有低关键级任务工作业,因此线下估计的整体调度比率较AMC-arb-x和AMC-max-x有所下降,而任务实际运行时的执行时间往往小于Ci值,低关键级任务的弱约束执行对高关键级任务的实际影响小于估计值,因此本文提出调度策略能够在保证高关键级任务正确执行的情况下提升低关键级任务的调度比率,从而减少丢弃任务的开销,提高资源利用率。此外,AMC-we-max-x策略的响应时间计算精确度较高,估计所得的任务集可调度比率整体高于AMC-we-x。在实际应用中,可以根据任务的性能分配弱约束模式中的参数值,为任务的服务水平提供多种选择。2.2 相关概念
3 优先级分配策略
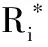
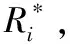
4 响应时间
4.1 干扰时间分析
4.2 响应时间的静态部分和关键等级切换部分
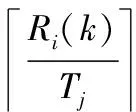
4.3 基于响应时间分析的传统调度策略
4.4 弱约束执行模式参数分配规则
4.5 两种调度策略的主要区别
4.6 AMC-we-x
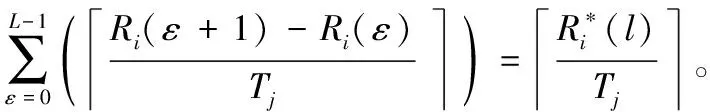
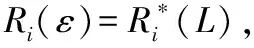
4.7 AMC-we-max-x
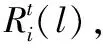
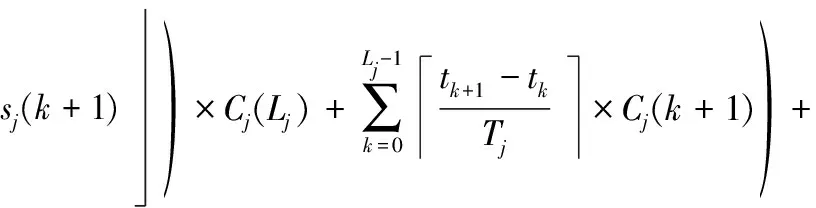
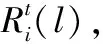
5 实 验
6 结 语

