一种满足可靠性和能效的云工作流调度方法

殷 越 隋丽娜

1(河南工业和信息化职业学院信息工程系 河南 焦作 454003) 2(河北民族师范学院数学与计算机科学学院 河北 承德 067000)

0 引 言

云计算[1]可以将分布于世界各地的互联网上的各种IT资源(计算、存储、带宽等)进行有效的整合，然后通过虚拟化技术以实时按需的形式提供给用户使用。云计算中的任务调度问题就是要实现任务与资源间的有效映射，在满足用户定义的时间或费用的约束下获得满足服务质量要求的调度解[2]。尤其是将科学工作流模型应用于云计算调度时，由于工作流结构的复杂性以及工作流中任务顶点间的相互关联性和依赖性，此时的调度算法将更为直接地影响任务调度的成功率[3]。

云计算环境中的科学工作流应用通常表现为海量数据密集型任务处理，主要特点表现为[4]：1) 任务提交与计算过程动态多变，通常是一种有向无环图DAG结构；2) 对调度可靠性要求更高，需要有效地满足调度可靠性机制，以提高调度成功率；3) 任务调度导致资源提供方的能耗加剧，任务调度过程中需要考虑能效调度机制。综合以上三点考虑，在大规模云系统中，工作流调度还需要考虑能效和可靠性问题。同时，为了实现可靠性工作流调度，需要重点解决：1) 如何量化任力调度时可靠性；2) 如何寻找满足最大化可靠性和最大能效的调度方案。

为了同步解决工作流调度的能效和可靠性问题，本文将设计一种新的工作流调度算法REEWS，将通过一种多阶段式的调度求解过程，得到了最优任务调度解。

1 相关工作

文献[5]通过赋予任务不同优先级，设计了异构最快完成时间调度算法HEFT，从而实现了任务调度时间最小化。文献[6]对HEFT算法进行了扩展，提出了一种基于失效约束的异构最快完成时间算法RHEFT，该算法将失效率与单个指令执行时间的乘积考虑至工作流调度中，以此作为映射任务的标准，并最大化系统的可靠性。文献[7]提出一种异构预算约束调度算法HBCS，通过定义代价因子调整可用预算与最低廉价格可能性的比例，实现调度优化。HEFT、RHEFT和HBCS均是以调度长度为单目标进行最优化，忽略了调度可靠性问题。文献[8]在考虑任务优先序列并结合复制的思想，提出基于可靠性的工作流调度算法CRB，算法可以有效实现执行时间与执行失败率的同步降低，提高整体可靠性。文献[9]同步考虑工作流的安全需求问题，在满足用户时间和成本约束的基础上，设计了安全约束算法PALS，并利用变近邻PSO对工作流调度最优化问题进行了求解，实现了寻优能力较强的可靠性调度。遗传算法GA是求解工作流调度多目标优化的另一种有效方法，文献[10]提出的双目标调度算法BGA同样是以执行跨度和可靠性作为优化目标，但算法执行过程中会违背任务依赖性并可能产生无效解。同时，传统的遗传算法对调度解的进化均是随机进行的，这会导致遗传寻优收敛速度较慢。综合分析，目前基于可靠性的云工作流调度算法的相关研究问题在于：1)从云资源方来看，工作流调度成功与否仅以任务成功率评估资源信誉度，忽略了资源在执行任务时因为时钟频率带来的任务执行不稳定性；2)对于任务本身而言，已有模型基于信誉度为任务分配相同可靠性，忽略了任务本身的差异性，以及在不可靠资源上执行时间越长，其成功率就越低的情况。

本文提出的算法目标是在维持任务依赖约束以及用户定义的截止时间期限约束的前提下，最小化工作流执行能耗和最大化调度可靠性。由于云计算环境的复杂性，物理硬件上的缺陷和温度过高的环境因素导致的系统失效是不可避免的，此时失效率极大地依赖于系统的运行频率和电压。然而，即使运行在最小频率也不能带来最小的失效到达率。因此，算法的目标是为处理器分配合适的电压/频率等级用于就绪任务的执行，使得任务执行的可靠性达到最优并耗能最少。

2 系统模型

2.1 云计算系统模型

云计算系统由m个异构物理主机PM集合组成，主机CPU均配置有动态电压/频率调整DVFS功能。假设每个PM/处理器提供k个频率等级(f1,f2,…,fk)，即可运行于不同的频率和电压等级，且忽略CPU进行频率转换的开销。处理元素间通过通信链路相连，通信链路间的通信带宽相同，且处理器之间的通信是完全可靠的。主机PM可通过虚拟化技术虚拟成若干台虚拟机进行任务调度。每台虚拟机也与主机一样可运行于不同的频率。对于这种由异构物理主机构成的云计算系统模型，每一个可用的物理主机在进行工作流任务调度时均可以作为任务调度的选择目标，并根据物理主机的CPU处理能力和资源分配状态进行任务调度目标的映射求解，比较适用于科学工作流场景下需满足能效的任务调度环境。

2.2 应用模型

通常，工作流应用是一种任务间具有关联性的并行应用模型，可定义为有向无环图DAG模型，表示为G(T,E)。该模型可以明确工作流结构中所有任务间的偏序关系，即前驱与后继关系，以此约束任务间的执行次序。T代表n个任务集合，ti∈T，1≤i≤n，E代表有向边集合，任务ti与任务tj之间的有向边ei,j∈E，1≤i≤n，1≤j≤n，i≠j。此时，任务ti是任务tj的父任务parent，任务tj是任务ti的子任务child。两个任务间的边的权重w(eij)代表任务ti与任务tj之间的数据传输量(只考虑在两个任务调度至不同物理主机上执行时)，每个任务分配一个权重w(ti)，代表任务的计算代价，即执行该特定任务时的指令数量，单位为百万指令数MI。

若任务满足parent(ti)=∅，即任务没有父任务，则该任务为工作流的入口任务；若任务满足child(ti)=∅，即任务没有子任务，则该任务为工作流的出口任务。工作流结构中的入口任务与出口任务在有向无环图中可以被明确表示，并且根据有向无环图模型，工作流调度算法设计中对于任务的调度选择也更加明确。本文相关符号说明如表1所示。计算代价w(ti)给出任务在任一主机上的执行时间ET，即ETi=w(ti)×CPI/fr,max，其中：fr,max表示任务执行时间处理元素的最大频率；CPI表示特定主机每个指令的CPU执行周期。两个关联任务间的通信时间CTij=w(eij)/bw(pmr,pms)，其中，bw(pmr,pms)代表通信链路的带宽，单位为Mbit/s。当两个任务执行于同一主机时，通信时间为0。此外，还有两个重要属性如下：

估计开始时间ESTi：代表任务ti在任一主机pmr上的开始时间，定义为：

(1)

式中：tp表示任务ti的父任务。

估计完成时间EFTi：代表任务ti在任一主机pmr上的完成时间，定义为：

EFTi=ESTi+ETi

(2)

表1 符号说明

2.3 功耗模型

云数据中心中，服务器的功耗主要由CPU、内存、磁盘存储器和网络接口构成。比较其他的系统资源，CPU消耗了最多的能源。本文将采用以下的功耗等式模型：

P=Ps+h(Pind+Pd)

(3)

式中：Ps表示静态功耗；Pind表示与频率无关的功耗部分；Pd表示动态功耗，与运行频率相关。

静态功耗Ps当系统处于开启状态时就会存在。该功耗维持时钟为活跃状态和内存处于休眠状态。参数Pind为常量功耗，在维持系统备用的情况下可降低至最小值。对于计算密集型任务类型，常量功耗为固定值，此时仅需要考虑动态功耗Pd，其与运行频率间的关系为：

Pd=CeffV2f=Cefff3

(4)

式中：Ceff表示有效负载电容；V表示供电电压；f表示运行时钟频率。时钟频率f与V成正比，若应用任务运行于低频率，则供电电压会线性降低。式(3)中，h的取值决定了系统状态。若h=1，则系统是活动状态；否则，系统处于休眠状态。由式(4)可知，频率相关的动态功耗取决于频率，且在满足条件fee=3(Pind/2Ceff)-3时可得到其最小值，即能效最优。因此，对于特定任务ti的能耗可计算为：

(5)

式中：ETi表示运行最大频率/电压时任务ti的执行时间。本文所有频率值均是根据等级设备的标准值，可对等地调整至最大值。最后，系统能耗为所有任务执行能耗之和，定义为：

(6)

该功耗模型同时考虑了服务器的动态和静态功耗，使服务器在任务调度过程中可以进行忙闲状态切换，最大限度地节省服务器能耗。同时，主要由CPU频率决定的能耗计算方式也可以更加准确地描述计算密集型工作流任务类型的能耗状况。

2.4 可靠性模型

应用任务执行过程中，硬件崩溃、软件缺陷、机器运行的高温等均可以导致系统永久或短暂失效。通常，短暂失效的概率远大于永久性失效。因此，本文在工作流调度过程中将考虑系统的短暂失效影响。通常，系统短暂失效服从泊松分布，而失效到达率λ则与计算节点的运行频率相关。由于计算节点的可靠性直接关系着计算密集型任务的计算可靠性，本文将忽略存储和网络接口的影响。失效率的关系式为：

(7)

式中：fr,op表示运行频率；λ0表示在最大频率/电压下的初始失效率；F(fr,op)表示频率的严格递减函数；d>0表示一个常量。由式(7)可知，当f=fmin时失效率λ最大，即处于最小运行频率(能耗节省最合适的频率)时失效率最大(可靠性最小)。d值越大表明失效率更容易受到频率/电压扩展的影响。因此，最大化可靠性和最大化能耗节省两个目标本质上是相关冲突的目标。

最后，系统可靠性为未失效状态下任务执行的概率。考虑在泊松分布下的失效率，任务ti(计算代价为ETi)运行于频率fr,op下执行的可靠性计算为：

(8)

所有工作流中n个任务的执行可靠性为：

(9)

该可靠性模型根据泊松分布将计算节点的可靠性建立为服务器处理频率的函数，同时结合前文的功耗模型，服务器功耗也主要由频率决定。如此，工作流调度的可靠性和能耗的最优化均与服务器频率相关，即可以将最优化模型描述为同一参数影响下的冲突式的多目标优化问题进行均衡求解。

2.5 问题描述

本文的目标是将n个工作流任务调度至m个异构主机上，在满足任务间的执行先后次序的基础上实现：1) 最大化系统可靠性；2) 最小化系统能耗；3) 满足用户定义的截止时间QoS约束。

3 基于可靠性和能效感知的工作流调度算法

3.1 算法思想

本文提出一种基于可靠性和能效感知的工作流调度算法REEWS，实现云计算环境中工作流调度时的系统可靠性和能耗最小化。算法的主要工作由以下四个阶段组成：

1) 计算任务优先级：寻找有效的工作流任务的拓扑排序，同时满足任务间的执行次序。

2) 任务聚簇：将任务划分为集合，从而最小化任务间的通信代价，进而最小化系统的能耗。

3) 截止时间分配：将用户定义的截止时间QoS约束在各任务间进行子划分。

4) 任务调度：将聚簇后的任务集调度至运行于合适频率/电压等级的处理器上执行，使得系统的全局可靠性最大化，且最小化系统能耗。

3.2 REEWS算法

REEWS算法过程如算法1所示。步骤2计算任务ti的平均执行时间ETi,avg和平均通信时间CTij,avg，步骤3计算系统中每个任务的最早开始时间EST和最早完成时间EFT，步骤5调用calculate_Priority(tentry)计算系统中每个任务的优先级，优先级采用自顶向下的方式从入口任务开始计算，直到出口任务。步骤6中Clustering()用于生成满足任务间先后执行次序的任务聚簇集，步骤7将全局截止时间分配至工作流的最后一个任务(出口任务)，步骤8中Allocate(texit)设置为真以确保最后一个任务已被分配子截止时间。步骤9调用Distribute_Time(texit)进行截止时间分配，步骤10-步骤16用于调度聚簇中的任务至提供最大化可靠性的处理元素上。对于在每个处理器上的每个聚簇，步骤12检测是否处理元素满足该聚簇的截止时间分配值，若满足则计算执行频率。步骤13计算在处理元素上聚簇中每个任务的执行可靠性。步骤15将聚簇调度至得到最大可靠性的处理元素上执行。

算法1REEWS-Reliability and Energy-Efficient Workflow Scheduling

Input:G(T,E) with a deadlineDand set of physical machines/processorsPM.

Output:Reliability and energy efficient schedule of workflow.

1.foreach tasktiinT

2. calculateETi,avgandCTij,avgon all processors

3. calculateESTiandEFTiby Equ.(1-2)

4.endfor

5.callcalculate_Priority(tentry)

6.cl←call Clustering(T)

7. SubD(texit) ←D

8. Allocate(texit) ←true

9.callDistribute_Time(texit)

10.foreach clustercli

11.foreach processor/physical machinepmrinPM

12. calculate energy efficient frequencyfkonpmrfortc(tc∈cli) by Equ.(5) such that it meets the SubD ofcli

13. calculate reliability oftconpmr(tc∈cli) by Equ.(8)

14.endfor

15. assignclito processing element providing maximum reliability

16.endfor

17.endprocedure

3.3 计算任务优先级

计算任务优先级次序可以确保关键任务被优先执行。任务优先级即是寻找调度任务的拓扑排序，同时需要满足任务间的先后次序。这样，遵守任务优先级的任务调度次序将肯定满足不同任务间的执行顺序关系。

首先考虑出口任务texit，由于没有任一父任务，其优先级为平均执行时间，进而利用该值递推其他任务优先级，定义为：

(10)

基于任务优先级，任务被置入任务队列task-list，该队列描述了任务在分配资源时所考虑的排序，进而可以获得满足执行次序的最小化调度时间。算法2是优先级计算过程。

算法2calculate_Priority(T)

1. initialize priority of exit task,prexit←ETexit,avg

2.foreachtiin reverse order

3. calculate the priorityPrifor each task as per Equ.(10)

4.endfor

5.endprocedure

3.4 任务聚簇

当任务被调度至不同的处理器上执行时任务间的数据传输将消耗大量能量。因此，算法3可用于任务聚簇,其主要目标是使得无相互关联关系的任务聚成一个簇，进而消除任务的通信开销，降低通信能耗。经过步骤3-步骤16，系统中的每个任务被分配至一个聚簇中。步骤4检测当前任务ti是否已被分配至一个聚簇中，若没有分配，则在步骤5中创建一个新的聚簇，并在步骤7中将任务添加至该新聚簇中。步骤8对任务ti的子任务进行排序，步骤9-步骤14寻找ti的一个已被添加相同聚簇的子任务。然而，仅在满足以下两个条件的情况下，ti的一个子任务tj才会被添加于相同聚簇中：首先，该任务必须仍未分配给任意聚簇，其次，tj的所有父任务已被分配至一个聚簇。步骤10的目标即是检测以上两个条件。若检测结果为真，则该子任务不被加至相同聚簇中。当不再有任务被添加至先前聚簇中时，控制过程进入循环外层的迭代中创建新聚簇。该过程重复至所有任务均被分配至一个聚簇中为止。

算法3Clustering(T)

1. add all taskstifromTintotask_list

2.k=0

3.foreach tasktiintask_list

4.iftihas not been assigned to any clusterthen

5.k=k+1

//make a new clusterclk

6.label:

7. add tasktito clusterclk

8. sort children of taskti

9.foreach chiletjof taskti

10.iftjhas not been assigned any cluster and parent(tj) has been assigned a cluster

11.ti←tjandgotolabel

12.break

13.endif

14.endfor

15.endif

16.endfor

17.endprocedure

3.5 截止时间分配

算法4用于将截止时间在所有任务间进行子分配。截止时间子分配与任务的完成时间成比例增长，可以用来降低处理器的执行频率，进而降低执行能耗。算法开始于已分配任务，即已分配截止时间D的出口任务开始执行。然后，所有未分配的关键父任务被逐步分配子截止时间。在此过程中，需要定义关键路径和关键父任务。

算法4Distribute_time(t)

1.whilethas unallocated parentdo

2.path←null,tk←t

3.whiletkhas unallocated parentdo

4.path←deciding_parent oftk+path

5.tk←deciding_parent oftk

6.endwhile

7.callallocate_SubD(path)

8.foreach tasktiinpath

9. allocate(ti)←true

10.endfor

11.foreach tasktiinpath

12. updateESTjwheretj∈chile(ti)

13. updateLFTjwheretj∈parent(ti)

14.callDistribute_time(ti)

15.endfor

16.endwhile

17.endprocedure

定义1从tentry至任务ti的最长路径为任务ti的关键路径。

定义2对于任务ti的未分配父任务tp，若满足EST(tp)+ETp,avg+CTpi,avg达到最大值，则该任务为关键父任务。

对于输入的有向无环图DAG，必须存在一条从入口至出口的关键路径。首先，所有DAG中关键路径上的关键任务根据其平均执行时间分配子截止时间。再根据任务的子截止时间向其所有未分配的关键父任务分配子截止时间。该递归过程将关键路径上的任务和其子截止时间作为输入，逐步向其未分配的关键父任务进行子截止时间分配。

算法4中，出口任务是输入任务，步骤2-步骤6从出口任务开始初始化，并递归向关键父任务迭代，直到没有未分配父任务留下为止。步骤7中，allocate_subD(path)被调用来向关键路径上的每个任务分配子截止时间。步骤8-步骤10中，在关键路径上的所有任务的allocate(task)变量设置为真。然后，步骤12更新子任务的最早开始时间EST的值，步骤13更新父任务的最晚完成时间LFT的值。步骤14中，再次递归调用本文算法将子截止时间分配至关键路径的所有未分配的父任务上。

3.6 任务调度

算法5用于向从起点任务至终止任务间的关键路径上的所有任务分配子截止时间。为了均匀地在路径上的所有任务间进行截止时间分配，计算关键路径的路径长度pl后，引入一个标准因子N：

(11)

步骤4-步骤7用于计算任务ti所在的关键路径的路径长度pl，步骤10中考虑任务的最终执行时间FET，利用标准因子N计算子截止时间分配值：

FET(ti)=ETi,avg+ETi,avg×N

(12)

步骤11中，在关键路径上的每个任务的子截止时间计算为：

SubD(ti)=EST(ti)+FET(ti)

(13)

算法5allocate_subD(path)

1.tstart←start task ofpath

2.tend←end task ofpath

3.pl=0

4.foreach tasktiinpath

5.pl=pl+ETi+CTij,tjis successor oftiin path

6.ti←tj

7.endfor

8. calculate normalized factor by Equ.(11)

9.foreach tasktiinpath

10. calculateFET(ti) by Equ.(12)

11. calculate SubD(ti) by Equ.(13)

12.endfor

13.endprocedure

任务调度将聚簇后的任务集调度至选择了合适频率/电压等级的处理器上执行，使得系统的全局可靠性达到最大化，且系统能耗被最小化。

4 实 验

为了验证REEWS算法的性能，通过仿真实验的手段分析工作流调度的结果，并与以下三种经典工作流调度算法进行性能比较：HEFT算法[5]，RHEFT算法[6]，PALS算法[9]。HEFT算法按照任务的秩值进行排序，然后按序选择任务，将其调度至执行时间最小的处理器上执行。RHEFT算法将失效率与单个指令执行时间的乘积考虑至工作流调度中，以此作为映射任务的标准，并最大化系统的可靠性。PALS算法则在非关键任务上利用DVFS技术降低了工作流调度的总体能耗。

4.1 实验配置

为了模拟云计算环境，利用CloudSim[11]平台构建IaaS云环境，该平台中已经扩展了内核，加入了能效感知调度方法。对于计算节点能耗模型，应用2.3节中介绍的功能模型。随机选择若干计算节点进行算法模拟，具体分布于4、8、16和32台计算节点。表2给出每个计算节点的相关参数，节点的最大运行频率处于1.6 GHz至2.8 GHz之间，对应于每个可执行的指令数MIPS为1 500至3 000之间。每个计算节点支持4个等级的动态频率/电压调整，分布于fmin至fmax之间，同时约定fmin=40%fmax。

表2 相关参数

仿真实验中引入两种工作流结构进行测试，包括随机生成任务图和高斯消除任务图两种结构。任务数量分布于20、40、60、80和100，任务中计算型和通信型任务的比例CCR值设置为0.2、0.5、1.0和1.2。

4.2 工作流结构

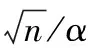
仿真实验中，随机任务图根据以上参数的不同组合进行生成。任务的计算代价MI均匀地分布在4 000 000～10 000 000之间，递增步长为7 000 000，形状参数分布于0.2、0.5、1和2之间。通信代价随机生成于计算代价与CCR值的乘积间，通过不同的CCR取值，工作流应用的结构类型也将有所不同。

2) 高斯消除任务图。高斯消除任务图可以通过改变计算代价与CCR取值决定。此外，矩阵大小m用于计算任务图中任务的数量。高斯消除任务图的结构是固定的，因此不需要任务数量和形状参数。对于高斯消除任务图，实验中将任务数量分布于9、20、35和65之间。

4.3 评价指标

1) 能耗：执行所有工作流任务带来的总体能耗，由式(6)定义。

2) 可靠性：在没有失效的情况下所有n个任务执行时系统的可靠性，由式(9)定义。

4.4 实验结果

1) 不同任务规模下的性能。比较工作流DAG中任务数量分别为20、40、60、80和100时的算法性能，如图1所示。REEWS算法比其他算法消耗了最少的能耗，随着工作流规模(任务数量)的增加，本文算法较HEFT和RHEFT在能量节省比例上分别增加了25%～31%和38%～44%，原因在于工作流任务间的相关性导致有空闲时槽的存在。HEFT和RHEFT的能耗较高，原因是两种算法仅分别关注了执行时间和调度可靠性问题。对于PALS，能耗仅是通过在非关键任务上利用DVFS进行能源节省，而本文算法则同时在关键和非关键任务应用DVFS进行降能，同时可以满足截止时间约束条件。因此，REEWS算法对PALS节省的能耗范围为10%～21%。观察可靠性情况，REEWS算法仍是所有算法中最优的。这是因为该算法在选择目标资源时考虑了调度失效率问题。进一步，算法选择了合适的运行频率/电压等级从而在任务执行过程中的可靠性达到最优。然而，在PALS中，可靠性被最小化，原因是它仅关注了能耗和执行时间的最优。HEFT和RHEFT的可靠性又优于PALS，原因是它们在执行任务时均采用了正常的处理器频率，虽然没有降低能耗，但没有牺牲可靠性。

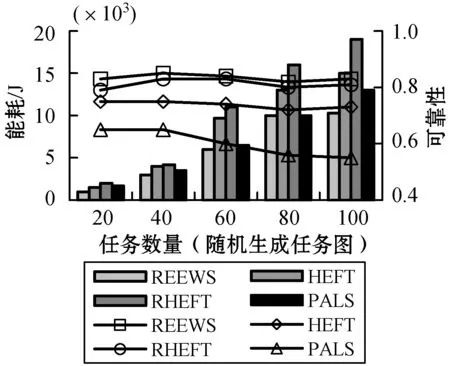
图1 任务规模对能耗与可靠性的影响

2) 不同处理器数量下的性能。本节观察处理器数量分别为4、8、16和32，任务规模固定为60时的性能表现如图2所示。随着处理器数量的增加，REEWS算法的能耗节省幅度也在增加。REEWS较HEFT的能量节省为16%～27%，较RHEFT的能量节省为22%～34%，较PALS的能量节省为7%～13%。这是因为更多的处理器可用时，单个处理器上的任务量会变少，改变其运行频率的概率将变高，进而可以降低总体执行能耗。然而，到达某一极限后，处理器数量的增加则无法进一步降低总体能耗，这是由于此时空闲处理器的能量开销有所增加。此外，REEWS的可靠性也是所有算法中最优的，这是由于更多的处理器可用时，该算法选择最优的处理资源的概率也将增加。

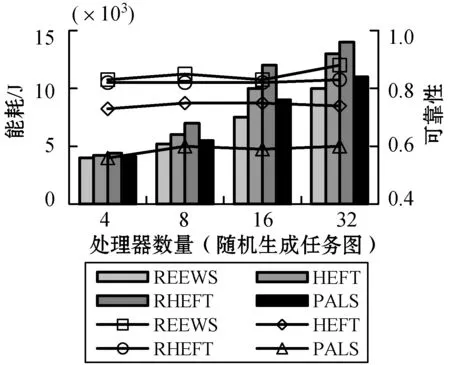
图2 资源规模对能耗与可靠性的影响

3) 不同CCR值下的性能。图3是不同CCR取值下，60个任务和8个处理器资源在随机任务图中得到的结果。对于CCR<1的情况，即计算密集型任务图，由于在计算密集型任务上使用了DVFS，因而得到了最小的能耗。REEWS比较HEFT节省了23%～30%的能耗，比较RHEFT节省了30%～34%的能耗，比较PALS节省了15%～20%的能耗。然而，当CCR>1时，本文算法相较三种算法仍可以分别节省约21%、28%和14%的能耗，原因是在数据通信阶段，本文算法能够使得处理器的运行频率达到最小。同时，还可以看到，REEWS的可靠性也是所有算法中最好的。

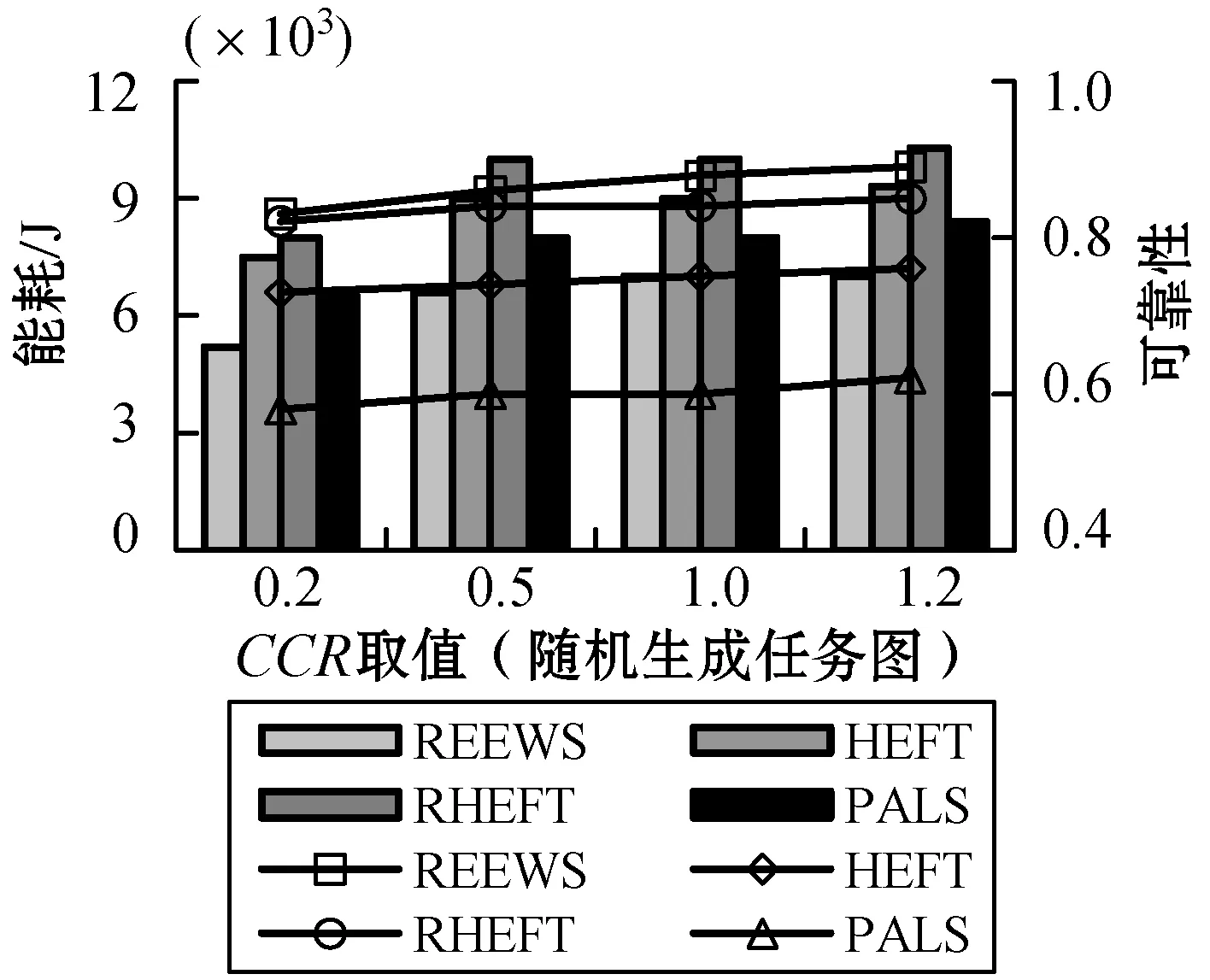
图3 CCR对能耗与可靠性的影响

高斯消除任务图的测试结果可见图4-图6，其结果与随机任务图的结果是相似的，综合说明本文算法在处理不同类型的工作流结构、规模时具有较好的适应性，可以在不同类型的工作流结构中进行高可靠性和高能效的工作流调度任务。

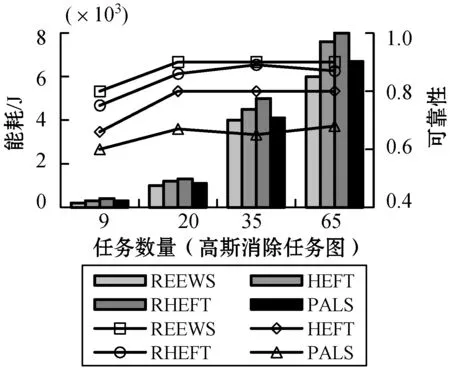
图4 高斯消除任务图下任务数量对性能的影响

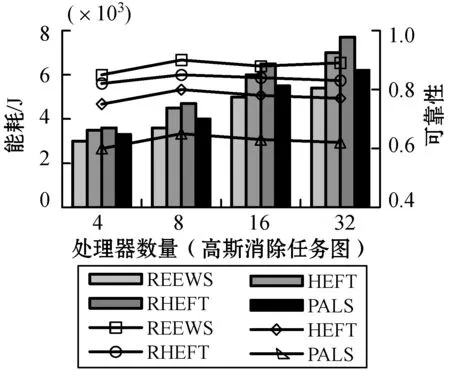
图5 高斯消除任务图下处理器数量对性能的影响

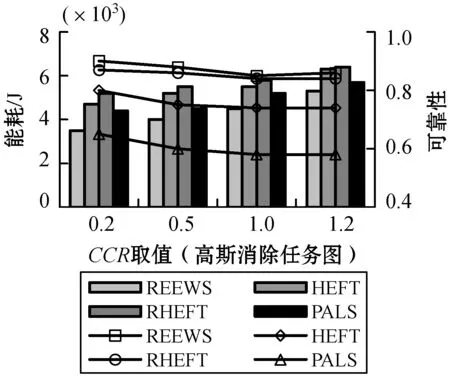
图6 高斯消除任务图下CCR取值对性能的影响

由以上实验结果可以看出，在不同的CCR取值下，即工作流中包含不同计算型和通信型任务比例的条件下，本文算法得到的能耗与可靠性并没有出现反转变化，说明本文算法可以适应于处理不同类型工作流任务的调度场景，具有较好的适应性。而在同步优化工作流调度能耗与可靠性上，本文算法也具有较好的可行性和鲁棒性。

5 结 语

为了同步解决云工作流调度时的失效和高能耗问题，本文提出一种工作流调度算法。为了在截止时间的QoS约束下最大化系统可靠性并最小化调度能耗，将工作流调度过程划分为四个阶段。第一阶段寻找有效的工作流任务的拓扑排序，同时满足任务间的执行次序；第二阶段将任务划分为集合，从而最小化任务间的通信代价，进而最小化系统的能耗；第三阶段将用户定义的截止时间QoS约束在各任务间进行子划分；第四阶段将任务调度至运行于合适频率/电压等级的处理器上执行，使得系统的全局可靠性最大化，且最小化系统能耗。随机生成任务图和高斯消除任务图的综合仿真测试结果表明，本文算法在降低总体能耗和提高工作流调度可靠性方面均优于对比算法。