基于刀具跳动误差的五轴侧铣加工精度预测模型构建
余杭卓,秦圣峰,2,丁国富+,江 磊,付建林
(1.西南交通大学 机械工程学院先进设计与制造技术研究所,四川 成都 610031;2.英国诺桑比亚大学 设计学院,纽卡斯尔 NEI 8ST 英国)
0 引言
五轴侧铣加工是指采用圆柱形、鼓形或其他形状铣刀的侧刃对工件进行铣削的加工方式。在加工过程中,刀具沿预定刀位轨迹运动,刀具回转形成的包络体与已加工表面成线接触,由切触线扫掠形成直纹面[1]。因此,如果刀具的刀位运动轨迹存在误差或刀具—工件接触轮廓存在误差,将导致零件表面产生加工误差。机床几何误差、装夹误差、热误差等会导致刀具运动轨迹偏离理想位置[2-4],刀具回转产生的跳动、刀具变形和磨损等会导致刀具回转轮廓误差[5-7]。因此,考虑多种误差源建立综合误差预测模型,实现加工精度的预测并进行误差补偿,是五轴数控加工技术精度控制的重要手段[8]。
许多学者针对五轴机床几何误差展开研究,分析了平动轴和转动轴运动中产生的多项误差,基于多体运动理论和齐次坐标变换建立了加工误差预测模型,并提出了补偿方法[9-12]。在此基础上,Zhang[3]、Weng[13]增加了机床热误差并建立了新的预测模型,这些模型有效地提升了加工误差预测精度。Arizmendi[5]针对侧铣加工刀具跳动对加工表面形状误差产生的影响展开研究,建立了表面形貌预测模型。模型中诸如刀轴线偏移量、倾角和偏心角等跳动参数的确定很关键,Arizmendi等[14]提出一种基于铣削力模型计算跳动参数的辨识方法。参考Arizmendi的模型,Kruger[15]和Artetxe[16]建立了考虑刀具跳动因素的刀具包络运动模型,该模型不仅分析了刀具跳动对表面形貌的影响,还研究了跳动参数与表面精度的映射关系,也进一步优化了跳动参数辨识方法。而这些辨识方法都是基于铣削力模型计算得到,因此,Kruger指出这种间接获取方法存在较大误差。张栋梁等[17]建立了考虑主轴—刀具安装误差的刀具轴线运动模型,该模型分析了主轴运动误差对刀具轴线运动轨迹的影响。Larue[18]和Islam等[6]研究了侧铣加工刀具变形对加工精度的影响,建立了精度预测模型。但刀具变形伴随有刀具磨损产生,Zeng[7]和Oliaei[19]综合刀具变形和磨损建立了加工精度预测模型,指出刀具变形和磨损存在耦合现象,该模型提升了表面加工误差预测精度。杨亚蒙等[20]基于齐次坐标变换理论建立了机床几何位姿与强力刮齿法向轮廓误差的映射模型,分析了机床运动轴运动误差对刮齿成形面精度的影响。
这些研究很好地分析了多种误差源对加工精度的影响,但是,针对五轴侧铣加工,较少有人同时考虑刀具运动轨迹误差和刀具回转轮廓误差对加工表面精度的影响,也缺乏相应的精度预测模型。本文在考虑机床几何误差、装夹误差等的刀位轨迹误差预测模型的基础上[21-22],引入刀具跳动产生的刀具回转轮廓误差,建立了新的误差预测模型。同时,提出一种试验方法获取了模型中的刀具误差参数。利用该模型可以计算加工表面刀触点分布,实现加工表面虚拟重构进而预测加工误差,为误差补偿提供重要参考。
1 侧铣加工误差分析
以整体式立铣刀侧铣加工为例,如图1a所示,刀具回转形成的包络体是一个理想的圆柱,沿预定刀位轨迹Lp运动。由于刀具回转速度远大于进给速度,刀具回转包络体轮廓与已加工表面形成一条与刀具轴线平行的切触线,这条切触线扫掠形成已加工表面,如图1b所示。
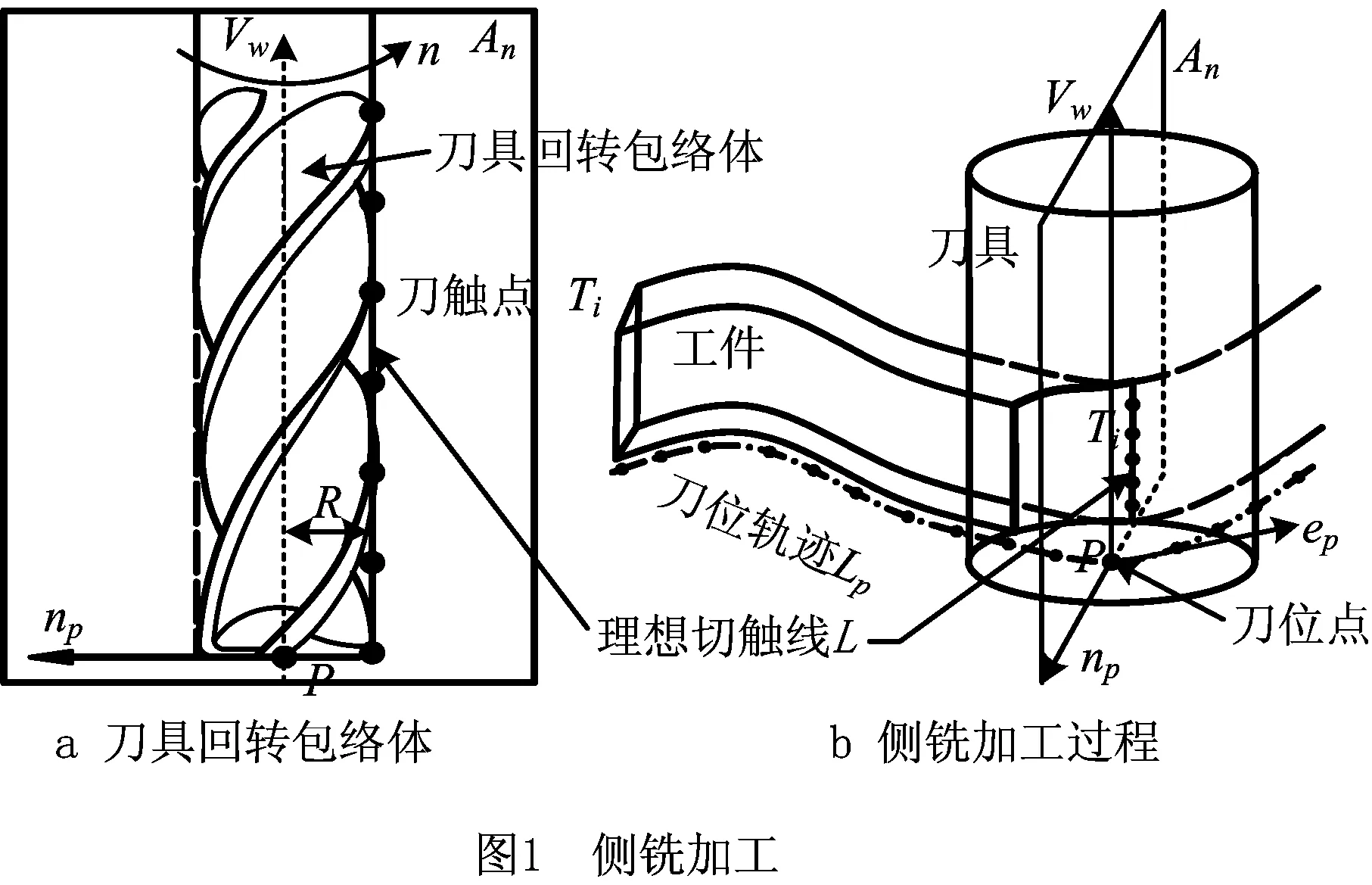


如图3a所示,刀具在制造和磨削过程中会形成径向半径尺寸误差,刀具安装后由于轴线偏心和刀夹间隙等因素,加上机床主轴回转产生的跳动干扰,造成刀具回转跳动的产生,即回转包络体半径偏离理想值。加工中伴随有刀具磨损和变形,造成径向回转半径误差等。这些刀具误差会导致刀具—工件切触线形状偏离理想位置,如图3b所示,切触线形状变化会导致扫掠面形状发生变化,进而影响表面加工精度。本文主要针对质地较软的材料如铝合金等铣削加工,加工时如果选择刚度较大的硬质合金刀具,则刀具磨损和变形较小,因此刀具回转轮廓误差主要由刀具跳动产生,且刀具—工件振动较小,在此忽略对加工精度的影响。
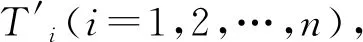

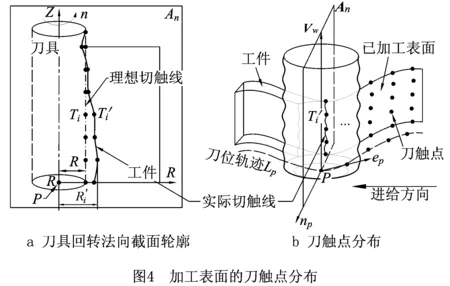
刀具运动过程中,在每一个刀位点处,切触线在表面留下系列刀触点,可建立模型计算这些刀触点坐标。因此,刀具完成所有刀位点运动,就可以获得整个加工表面的刀触点分布(如图4),由这些刀触点可以分析表面形状并计算轮廓误差。
2 预测模型构建
2.1 基于多体系统理论的刀位轨迹误差计算


(1)
(2)
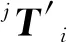
2.2 刀触点计算

(1)切矢的计算

ep=(epx,epy,epz)T=P1-P,
(3)
(4)

(2)单位法矢的计算

(5)
(6)
(3)刀触点计算
理想刀触点Ti对应的刀具回转半径均为R,理想的切触线应该是平行于刀轴矢量且与刀轴矢量间距为R。因此,不考虑误差的条件下,Ti的坐标可由式(7)计算得到。
(7)
式中Zi为各点的轴向高度,Zi=i·d。
(8)
根据刀位P点的系列刀触点计算流程,可以计算得到刀位轨迹上各个刀位点对应的理想系列刀触点和考虑误差的实际系列刀触点坐标。这样就可以得到整个扫掠面上的刀触点分布,这些点可以为后续表面形状和加工轮廓误差分析提供参考。
综上所述,针对五轴侧铣加工,同时考虑刀位轨迹误差和刀具回转轮廓误差的精度预测模型构建流程如图6所示。

3 刀具误差参数获取
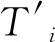
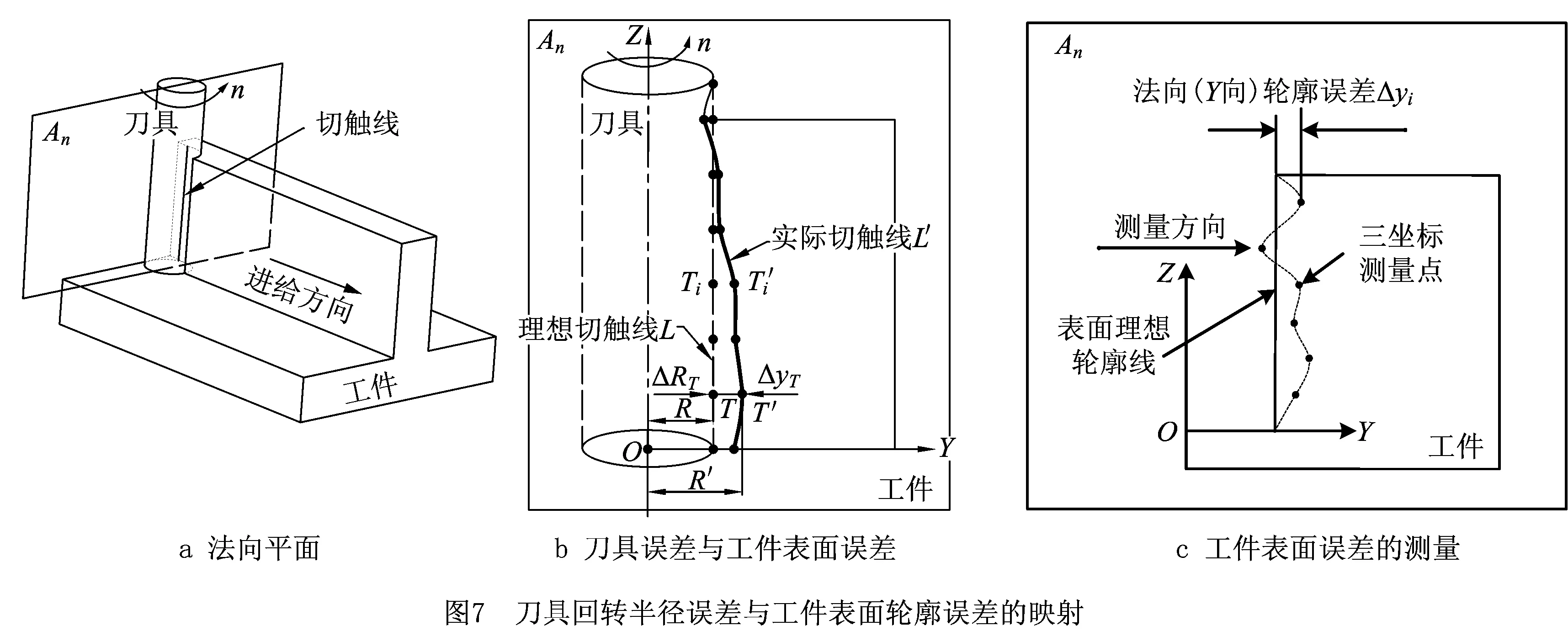
设T′对应的刀具回转半径误差为ΔRT,采用三坐标测量机沿加工表面法向(Y轴)测量表面上T′点对应的法向轮廓误差为ΔyT,如图7c所示。则有
(9)
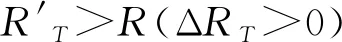
(10)
4 验证试验
为验证本文所提精度预测模型的有效性,进行铣削试验。加工机床为一台GMC820u加工中心(XFYZBA结构),铣削材料为铝合金6061,选用的铣削刀具及相关参数如表1所示。

表1 刀具相关结构参数

续表1
先进行平面铣削试验,获取刀具实际回转半径。如图8a所示,进给方向设置X轴,垂直于加工平面设置Y轴(法向),刀轴方向设置Z轴,在工件表面端面处沿刀具轴向(Z=3 mm,6 mm,…,45 mm)等间距设置15个测量点,间距d=3 mm。主轴转速为2 500 r/min,径向切深为1 mm(由于工艺参数的变化对刀具回转半径影响不大,后续加工中的加工参数不用与刀具半径测量试验的工艺参数严格保持一致),加工与测量如图8b与图8c所示。



这种基于试验的刀具回转轮廓误差参数辨识方法简单实用且精度较好,避免了复杂的理论推导,能较好用于工业实际中刀具回转轮廓误差的获取。
获取刀具实际回转半径后,分别加工专用于五轴侧铣精度检验的“S”件(ISO 10791-7)和内拔模15°的NAS979圆锥台试件(ISO 10791-7)[23],刀位轨迹如图10所示。加工工艺参数为:主轴转速n=2 500 r/min、进给速率Vf=1 000 mm/min、径向切深ae=1 mm。

基于加工NC代码,运用前述综合误差预测模型,可以计算得到理想加工表面的刀触点分布和考虑误差条件下实际加工表面的刀触点分布,图11为“S”件局部表面的刀触点分布。
如图11所示,局部表面上的理想刀触点和实际刀触点存在位置偏差,根据刀触点的位置信息可以实现加工表面虚拟重构,计算各实际刀触点对应的法向轮廓误差(计算方法见文献[21]),以评价加工精度。
分别选择两个试件表面上15个刀触点作为分析对象,并计算了这些点的法向轮廓加工误差。为验证本文模型的有效性,在此计算了两组误差预测值:第一组是基于本文提出的模型(同时考虑刀位轨迹误差和刀具回转轮廓误差,如图12a和图13a中的No.2曲线);第二组是基于文献[22]的模型(不考虑刀具误差只考虑刀位轨迹误差,如图12a和图13a中的No.3曲线),两图中的No.1曲线为运用三坐标测量机(Coordinate Measuring Machine, CMM)测量得到实际加工表面上相应点位的法向轮廓误差。两组预测值与实测值及两组预测值的预测误差对比如图12b和图13b所示。

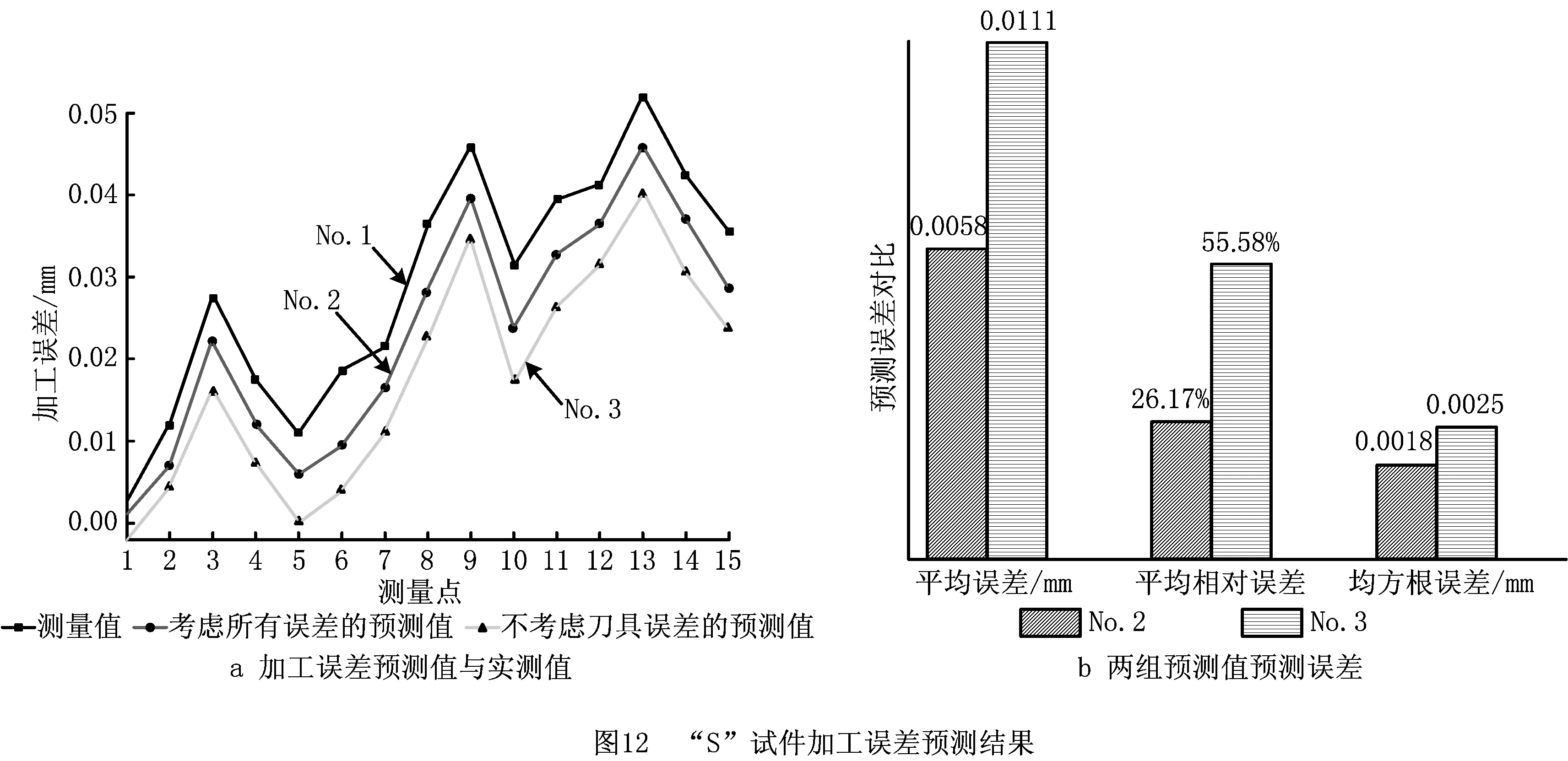

由图12和图13可知,新建模型的预测精度明显高于现有模型,说明刀具回转轮廓误差对加工精度产生影响。对于五轴侧铣加工精度预测,诸多模型[2-3,22,25-26]考虑了机床误差引起的刀位轨迹误差,并未考虑刀具回转轮廓误差对加工精度的影响。本文在此基础上引入刀具回转轮廓误差建立的综合误差预测模型提升了侧铣加工误差预测精度,为后续刀具误差补偿提供了参考。同时,该模型是一个开放的模型,能继续引入刀具磨损和变形等其他误差因素。
5 结束语
本文在现有刀位轨迹误差预测模型的基础上,引入了刀具跳动产生的刀具回转轮廓误差,并建立了一种新的综合误差预测模型。该模型在同时考虑刀具运动轨迹误差和刀具回转轮廓误差的影响下,计算加工表面系列刀触点分布,能够实现加工表面重构,并能有效预测表面加工误差。通过对比试验可以发现,相比现有模型,本文建立的模型能提升加工误差预测精度,为后续误差补偿及加工误差的控制提供了参考。针对刀具跳动引起的回转轮廓误差难以获取的情况,设计了一种试验方法,从而准确获取刀具轴向各点对应的回转半径,用于预测模型的计算。
由于本文研究的铣削材料主要针对质地较软的铝合金材料,刀具误差以跳动为主,对于硬度较大的钛合金、不锈钢等材料,还需要考虑刀具变形、磨损及刀具—工件振动等误差进行加工精度预测研究。

