基于HMM-SVM旋转风电装备叶片覆冰状态的评估

张惠，董映龙，成斌，李西洋，贾育豪，李兴图

(石河子大学机械电气工程学院/农业农村部西北农业装备重点试验室，新疆 石河子 832003)

随着国际社会对能源安全、生态环境等问题的日益重视，风能已成为可再生能源中发展最快的清洁能源。冬季气候寒冷的“三北”地区和湿度较大的东南沿海地区风能资源丰富，是我国风电开发的热点区域，“三北”地区风电装备叶片的覆冰问题已成为阻碍风电行业发展的关键因素之一[1-3]。风电装备叶片覆冰不仅导致机组功率损失，增加叶片的疲劳，降低叶片使用寿命，严重时还造成叶片损坏甚至风电装备倒塌，危及人员生命及财产安全[4-9]。

目前，国内学者在覆冰状态评估方面针对风电装备叶片的研究较少，多以输电线路为研究对象，采用神经网络、灰色理论、马尔科夫过程理论、仿真软件及在线监测系统等方法进行研究[10-11]。风电装备叶片工作环境恶劣，其覆冰过程受众多因素的影响，属于非平稳的随机过程。隐马尔科夫算法(HMM)能够分析动态时间序列，基于学习问题和编码问题对相邻状态间的关系进行模式识别，更大程度反映同类样本间不同样本的相似性[12-13]；SVM在解决小样本、非线性及高维模式识别问题的二类分类方面具有独特优势，其将相似的样本以尽可能大的欧式距离隔开，能更大程度反映类别样本间的差异性[14-15]。本文充分发挥HMM算法和SVM方法的优势互补性，以旋转风电装备叶片覆冰监测系统为基础，提取旋转风电装备叶片覆冰振动特征值，输入至HMM-SVM模型，以实现风电装备叶片覆冰状态快速、准确识别。

1 基于HMM-SVM的风电装备覆冰状态评估模型

1.1 HMM基本原理

HMM是关于时序的概念模型，描述了由一个隐含未知参数的系统所处状态到另一个状态的转换时产生状态随机序列，再由各个状态生成一个观测而产生的观测随机序列的过程。HMM可以用2个状态集合和3个概率矩阵来描述，即

λ=(N,M,π,A,B),

(1)

式(1)中，N为隐藏的马尔科夫链随机生成的不可观测的状态数，M为所有可能的观察状态数，π为初始状态的概率矩阵，A为马尔科夫链的状态转移矩阵，B为观测状态生成的概率矩阵。

为解决HMM的评估、解码和学习三个基本问题，采用前向算法计算在某个特定的HMM下一个可观察序列的概率，最有可能隐藏状态序列是根据可观察序列通过Viterbi算法得到，Baum-Welch算法决定最有可能产生某个观察集的隐马尔科夫模型,其中Baum-Welch算法过程如下：

(2)

(3)

(4)

式(3)、(4)中，aij为状态转移概率(1≤i,j≤N)，bjk为观察状态在隐藏状态下生成的概率(1≤j≤N,1≤k≤M)。

1.2 SVM评估模型

支持向量机(SVM)是一种针对小样本和少样本情况下的机器学习的新方法,是基于结构风险最小化的原则寻找基于线性可分条件的最优分类超平面[16]。首先给定一个样本集

(5)

式(5)中xi、yi分别代表2组数据所属的类别，R为实数集。

寻找最优超平面的问题可转化为解决基于约束条件的二次规划问题，优化条件是两类别之间的最短距离，最优超平面定义为

f(x)=k(x,xi)+b,

(6)

式(6)中，k(x,xi)为核函数，构建最优超平面可视为找到全部非零的αi，与一个非零αi对应的任意xi就是所求最优超平面的SVM。

为确保分类的准确性，引入松弛因子ξi≥ 0(i=1,2,…n)，则优化问题可以表示为：

(7)

式(7)中，w为权重向量，b为偏置向量，c为惩罚因子。

由最优化条件(KKT)定理可知，最初求解最优超平面的问题等同于求解二次优化问题，即

(8)

拉格朗日算子αi可通过求解上式中的函数得到，偏置b可通过任何一个已知支持向量xk及其所对应的αk计算得到，以便判断未知类型样本x所属的类别。

1.3 HMM-SVM模型

建立基于HMM-SVM的风电装备叶片覆冰状态评估模型的流程如图1所示。先获取风电装备叶片覆冰叶片振动信号样本，划分覆冰状态，再将收集到的样本分为训练样本和测试样本，并从样本中提取振动信号，通过信号处理和数据分析，识别关键因素构成特征向量；然后在HMM模型中输入特征向量并进行训练，得到与划分好的各覆冰状态相对应的HMM模型。通过Viterbi算法计算序列的概率，且舍弃概率值较小的部分，保留概率值大的样本，以降低其他因素干扰，确保所得结果的精确性；最后在SVM分类器中输入保留样本并进行识别分类，即可得到状态识别结果。

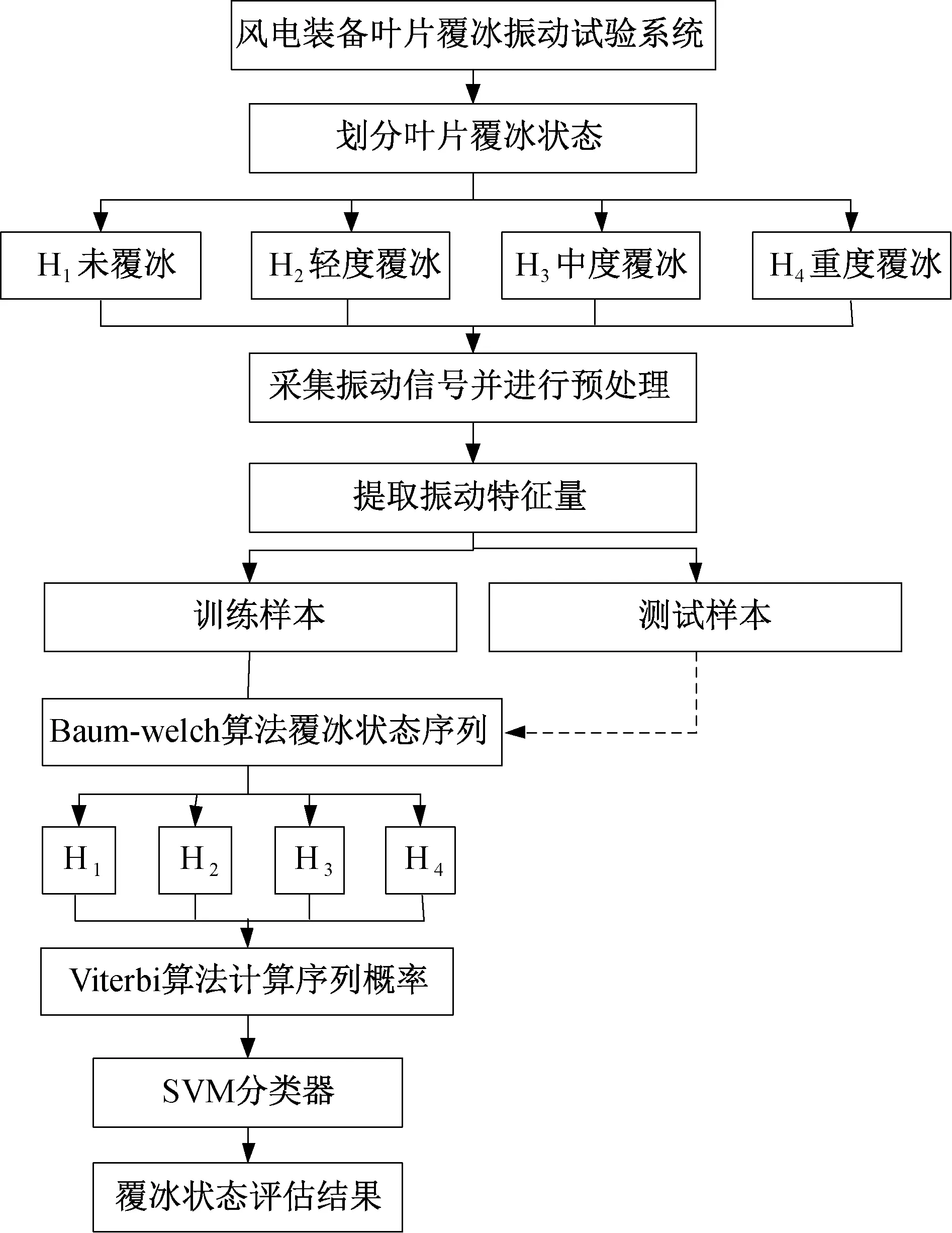
图1 HMM-SVM风电装备叶片覆冰状态评估流程

2 风电装备叶片覆冰振动信号的分析

旋转风电装备叶片覆冰振动测试试验台的搭建见图2所示。

试验在冬季自然环境中进行，所用风电装备叶片模型为按1∶12.5等比例缩小制作的1.5 MW风电装备，采用NACA4412翼型，叶片基体材料环氧树脂，增强材料为玻璃纤维，叶片铺层方式与商用NACA4412翼型叶片一致，叶片展长1.6 m，质量11.09 kg。

选择CT1010SLFP型三轴加速度传感器采集振动数据，传感器质量50 g，适用温度范围：-40～120 ℃，试验选取分布于叶片气动中心线上的4个测点，由环氧树脂胶胶黏分布于距离叶根0.32、0.56、0.88、1.36 m处，以叶片在摆振方向的传感器数据作为研究对象。

本文研究所用试验装置及试验环境均按照风电装备实际运行状态设计，在旋转风电装备叶片覆冰状态评估过程中以叶片不同覆冰厚度的振动信号为基础。叶片转速为60 r/min，即转频频率为1 Hz。

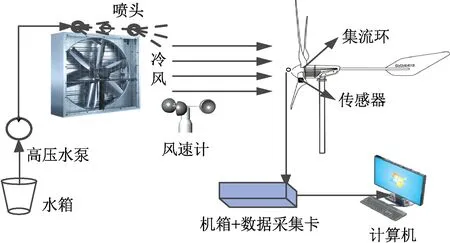
图2 旋转风电装备叶片覆冰振动测试试验台示意图

试验结果表明，叶片前缘最先覆冰，叶尖处覆冰量最大，叶根处覆冰较少。

分析旋转风电装备叶片叶尖覆冰厚度为0、2、6、10 mm时振动信号的时域和频域，结果(图3)显示：随着叶片运行时间的增加，覆冰厚度不断增加，叶片振动加速度逐渐增大，致使叶片振动能量整体呈递增趋势。

图3 不同覆冰厚度时叶尖振动信号频谱图

观察在不同覆冰厚度时旋转风电装备叶片的时域和频域波形,分析其振动呈现周期性变化(图4)可知：在覆冰条件下，叶片振动峰值主要分布在10～45 Hz频率范围内，主要为低频振动；振动信号周期性在叶片覆冰厚度为0、2 mm时相对不明显，幅值较大的为低频分量；随着叶片覆冰厚度由0增长至10 mm，其振动加速度由0.058 m/s2增加至0.147 m/s2；在330～360 Hz频率范围内，风电装备叶片振动出现较小峰值，究其原因是风轮挂机运行存在的轴向窜动效应和圆盘效应，导致叶片的振动加速度增大。

总体上，覆冰叶片振动方式主要为低频振动，随着叶尖处覆冰厚度的增加，其最大振动响应所对应的振动频率逐渐降低，幅值增加，对叶片振动响应影响最大的因素为叶尖处覆冰厚度的变化。

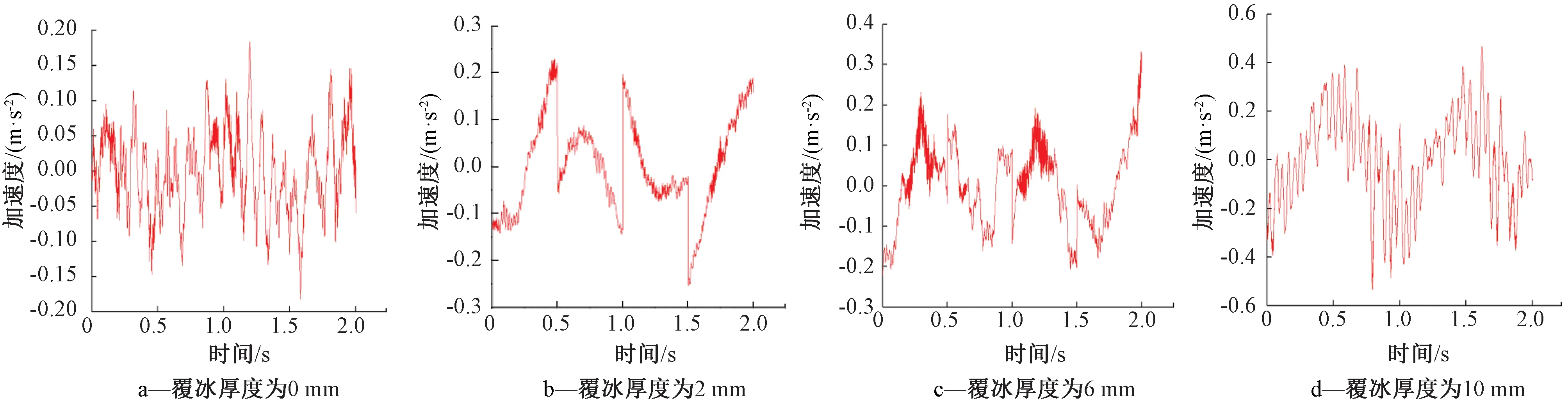
图4 不同覆冰厚度时叶尖处的振动响应

3 基于HMM-SVM的叶片覆冰状态评估实验结果分析

3.1 确定特征向量

根据旋转风电装备叶片覆冰振动测试试验结果分析，覆冰条件下旋转风电装备叶片的振动频率与覆冰厚度之间存在映射关系。风电装备叶片覆冰引发叶片翼型和气动性能的变化，叶片摆振加剧，产生较大的振幅甚至发生共振。因此，通过分析旋转风电装备叶片摆振方向振动信号的频域和时域，最终提取时域峰值XPi、频率均方根RMSi、速度V及位移S作为HMM-SVM模型的输入参数，构造特征向量。

3.2 确定训练样本

随机选取风电装备叶片覆冰的4种状态各50组样本向量作为训练样本，将4种覆冰状态各剩余的30组样本作为测试样本，部分振动信号特征数据如表1所示。

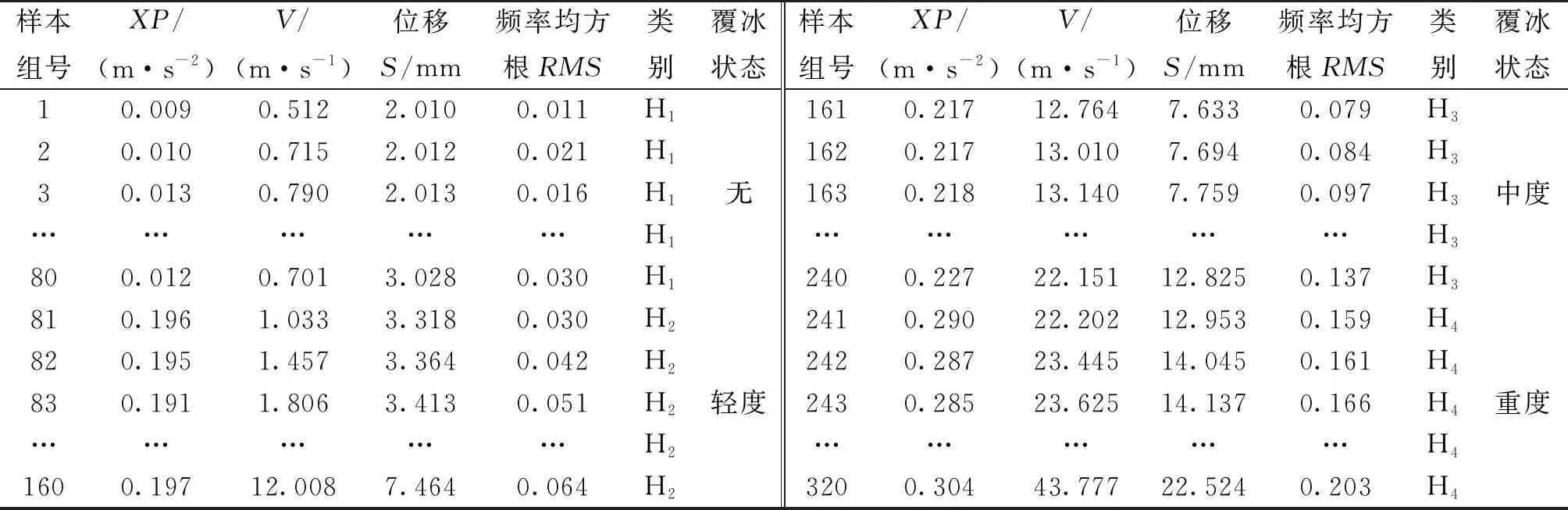
表1 部分振动信号特征数据

3.3 基于HMM-SVM的叶片覆冰状态评估模型的建立及结果分析

依据图1的流程建立HMM-SVM的叶片覆冰状态评估模型，具体步骤如下：

(1)以特征向量作为观测序列，输入至训练优化后的HMM模型中。

(2)通过Viterbi算法计算每个覆冰状态HMM模型中观测值序列出现的概率P(O|λn)(其中n是覆冰状态类型数，n=1,2,3,4)。

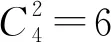
(4)SVM中的核函数选用高斯径向基函数，惩罚因子c及核函数的优化选择采用了交叉验证法。

(5)通过式(8)判断捕捉到的未知类型样本x所属的覆冰状态类别。

(9)

(10)

式(9)、(10)中，i为叶片覆冰状态类型，n是覆冰状态类型数，mi为叶片覆冰状态评估实验结果组数，Mi为叶片覆冰状态评估实验结果组数，P为覆冰状态识别准确率。

将风电装备叶片4种覆冰状态各30组样本进行覆冰状态评估实验，分别采用HMM模型和HMM-SVM模型进行覆冰状态评估，式(9)用于计算利用某种模型得到的叶片某个覆冰状态的识别准确率，式(10)用于计算利用某种模型得到的叶片覆冰状态的识别综合准确率。

评估实验结果如表2、图5所示。

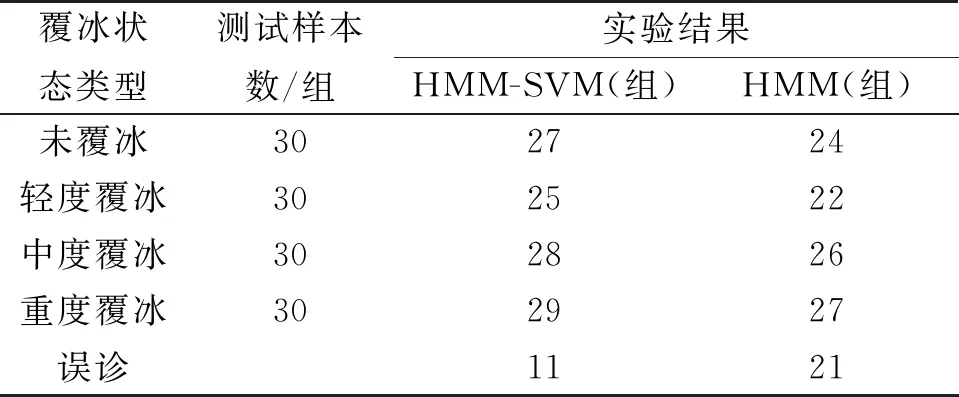
表2 两种模型叶片覆冰状态评估实验结果

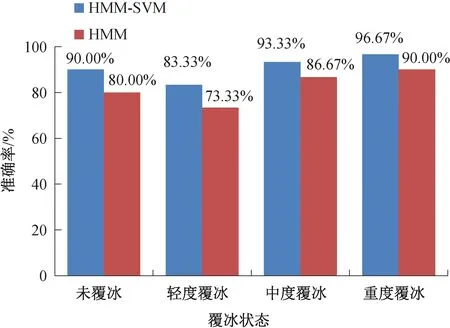
图5 两种模型叶片各覆冰状态评估准确率分析

由表2可知：基于HMM-SVM模型对于风电装备叶片覆冰状态的识别综合准确率(90.83%)高于HMM模型的综合准确率(82.50%)，且受其他因素影响更小，其健壮性更强。

由图5可知，风电装备叶片覆冰状态评估数据在轻度覆冰时评估相对误差较大。这是由于风电装备叶片在实际运行中，覆冰厚度较小时覆冰对风电机组的运行影响较小。因此，该模型在风电装备叶片覆冰运行过程中能够满足状态评估的要求。

4 结论

本文通过搭建旋转风电装备叶片覆冰振动测试系统，以提取的旋转风电装备叶片在4种覆冰状态下的振动信号特征值为基础，基于HMM-SVM算法建立了旋转风电装备叶片覆冰状态评估模型，并利用试验数据对评估结果进行了验证，得出以下结论：

(1)覆冰条件下，旋转风电装备叶片叶尖前缘覆冰程度最大。随着覆冰厚度增加，叶片振动响应变化显著；随着叶尖处覆冰厚度由0 mm增加至10 mm，叶片振动加速度由0.058 m/s2增加至0.147 m/s2。

(2)利用本文建立的基于HMM-SVM的旋转风电装备叶片覆冰状态评估模型对共计120组试验样本数据进行测试，评估准确率高达90.83%，验证了该模型的准确性和有效性。

(3)HMM-SVM模型比单一的HMM模型对于旋转风电装备叶片覆冰状态评估准确性更高，它充分结合了HMM模型在动态时间序列处理上的优势和SVM强大的分类能力，在风电装备叶片覆冰状态评估预测具有一定的应用参考价值。