无人机复杂电磁环境频谱特征反演测量

郭淑霞 吴义春 王江宇 高培伟

（1.西北工业大学无人机特种技术重点实验室，陕西西安710065；2.西北工业大学自动化学院，陕西西安710065）

1 引 言

在实际的战场环境中，电磁场分布复杂多变，实测电磁场数据与电磁传输环境、辐射源属性之间的关系十分复杂。无人机在执行任务的过程中会受到各种电磁干扰信号的影响与威胁，如何准确地对无人机典型用频频段电磁信号进行频谱特征反演，并根据反演结果对无人机典型用频装备抗干扰设计提供依据十分重要。

国内外对相关方法有一定研究，国外Urkowitz Harry 提出能量频谱检测算法，其核心是计算信号在特定时间内的能量，与预先设定好的门限值进行比较，做出判断，获得检测结果，Mahamadou，H.在直接探测光纤传输系统的研究中发现，光谱反演有利于改善接收端信号的质量［1］，Yarman，C.E.在处理核磁共振信号方面提出了一种新的信号反演方法［2］等；国内杨东凯通过对北斗反射信号的反演提高了有效波高和风速的反演精度［3］，王玉辉对短波信号的进行反演完成了对中国电离层电子密度图的重构［4］等。

本文提出了一种复杂电磁环境信号频谱特征的反演方法。该方法基于小波变换原理对无人机典型用频频段电磁信号进行变换处理，对其频谱特征进行奇异性检测，结合信号降噪处理去除频谱伪奇异点等对接收信号频谱特征进行反演测量。

2 电磁环境频谱特征反演测量原理

电磁环境频谱特征反演测量原理如图1 所示。

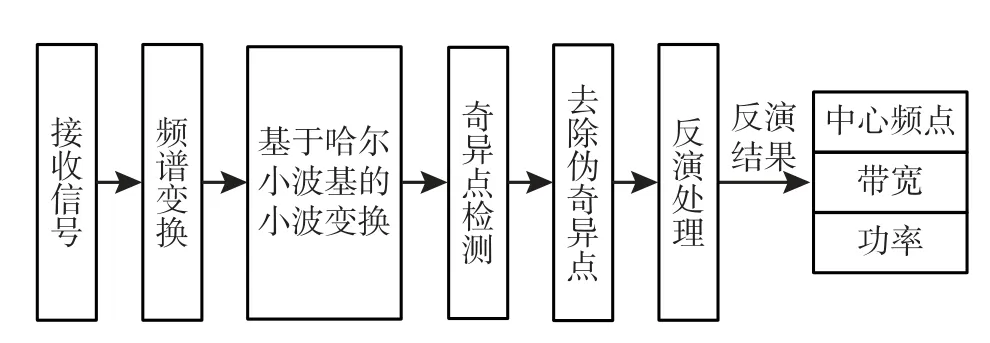
图1 电磁环境频谱特征反演测量原理Fig.1 Principle of spectrum characteristic inversion measurement in electromagnetic environment

图1 中，设接收信号为无人机运行环境中的用频设备频段的电磁信号，首先对该信号进行预处理，再对信号进行小波变换，基于小波变换结果进行信号奇异性检测，对信号降噪处理以去除伪奇异点，设置奇异点判决门限获得正确的信号奇异点，结合信号频谱可以对电磁信号频谱特征进行反演解算，得到电磁信号的中心频点、带宽和功率。该方法的核心在于小波变换基函数确定，奇异性检测和伪奇异点去除方法。

2.1 小波变换基函数确定

一维哈尔小波变换［5］的基函数是哈尔基函数，哈尔基函数是最简单的基函数，它是由一组分段常值函数（piecewise-constant function）组成的函数集，其表达式如下。

一维哈尔小波的母函数（mother wavelet）可以表示为

其对应的尺度函数（scaling function）可以表示为

其中，哈尔小波具有以下三种特性。

1）任何函数都可以由φ（t），φ（2t），φ（3t），...，φ（2k×t）以及它们的位移后得到的新的基函数所组成；

2）任何平均值为零的函数都可以由φ（t），φ（2t），φ（3t），...，φ（2k×t）所组成，即任何函数都可以由常数，φ（t），φ（2t），φ（3t），...，φ（2k×t）所组成；

3）哈尔小波具有正交性，可以表示为

由于哈尔基函数具有上述特性，在对复杂电磁信号的小波变换中可以监测到异于噪声的电磁信号，为频谱特征的反演提供基础。

2.2 信号奇异性检测

在小波变换基础上，信号奇异性检测［6］需要确定奇异点的位置和奇异指标，奇异性信号按奇异程度可分为剧变奇异信号和缓变奇异信号，通常利用李氏指数［7］（Lipschitz）描述信号的局部奇异性强弱。

设n是一个非负整数，n＜α≤n+1。如果存在两个常数A和h0（h0＞0），以及n次多项式Pn（h）使得对任意的h≤h0，均有

则称函数f（x）在点x0处的李氏指数为α。

对于采集到的接收信号做傅里叶变换得到其功率谱密度函数^Sx（f）［8］，再对得到的功率谱密度函数^Sx（f）进行哈尔小波变换，并对其结果进行求导，得到一阶导的模极值点所对应的频率点即为功率谱密度变化的奇异点，即为信号在采集目标频段内的出现频点和结束频点，求导公式为

式（5）中，先对采集频段内信号的功率谱密度函数进行哈尔小波变换，再对哈尔小波变换后得到的结果求其一阶导数的模极值点，则可以得到采集目标频段内信号的频率奇异点为

一组模极值点可以在频谱中唯一确定一个信号，模极小值点对应信号的起始频点，模极大值点对应信号的结束频点，模极值点相减可以得到信号反演带宽，模极大值点与模极小值点的中点为信号的中心频点，根据帕森瓦尔定理对模极值点内的信号功率谱密度函数求积分可以得到信号的功率。

2.3 伪奇异点去除

复杂电磁环境中，背景噪声的存在使电磁信号在小波变换后会产生伪奇异点，影响电磁信号频谱特征反演的准确性。为了去除伪奇异点，需要对信号平滑降噪处理和设置奇异点判决门限。

首先利用等距五点三次平滑公式对电磁信号进行平滑处理，得到电磁信号第i个采样点的数据值Yi的改进值

然后利用小波变换去噪原理对平滑后的电磁信号作去噪处理。其基本问题为小波基函数的确定、阈值函数的选择及分解尺度的确定。哈尔小波基具有正交性、紧支撑性和对称性，有利于小波去噪的实现，启发式阈值函数能够很好地保留大的信号小波系数，去除与信号小波系数相比较小的噪声的小波系数，选择合理的分解尺度在保证去噪质量的同时，可以减少小波去噪计算的复杂度。

奇异点判决门限的设置较为复杂，因为频率奇异点不仅与信号功率谱密度的形状有关，而且与其幅度有关，将小波变换结果进行归一化，然后设置合适的门限。

对于奇异点判决门限设置，设Δ为功率谱密度的平均值，则多尺度小波变换的归一化乘积为

设γe表示判决门限，针对固定的FFT 大小Nf，整个频率范围的起止点和子频段相邻处的边缘节点集合Ω 判决规则为

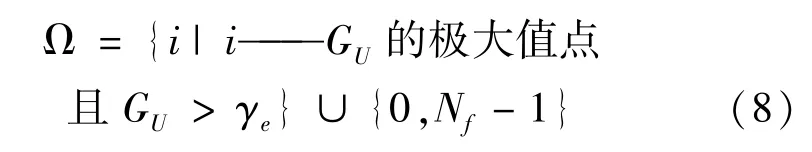
幅值高于判决门限γe的奇异点作为信号奇异点用于反演解算处理，得到反演的信号带宽、中心频点和功率。

通过对信号平滑去噪处理和设置奇异点判决门限，可以在信号奇异性图中准确地判断出信号奇异点，从而可以提高信号频谱特征反演测量结果的准确度。

3 算法仿真与验证

算法仿真原理如图2 所示，在设定的仿真条件下，包括信号体制、信号带宽、中心频点和信号功率，仿真发射信号；采用三种仿真方式，一是数字仿真，二是注入式仿真，三是辐射式仿真；在接收端对仿真信号进行反演处理，得到反演后的信号带宽、中心频点和信号功率。通过对反演后的上述参数与发射信号的相应参数进行比对分析，验证频谱特征反演方法。

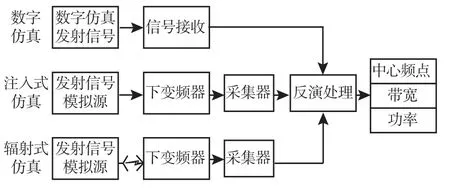
图2 算法仿真验证原理图Fig.2 Schematic diagram of algorithm simulation verification

3.1 数字仿真条件及反演结果

仿真条件:发射信号为一个信号，发射信号带宽1.35MHz，中心频点10MHz，功率-20.5859dBm。反演结果如图3 所示。

反演解算得到的信号频谱特征为:带宽1.345MHz，中心频点10.028 0MHz，反演功率-20.607 8dBm。反演带宽与设定条件的差值为0.005MHz，中心频点与设定条件的差值为0.028 0MHz，功率与设定条件的差值为-0.401 7dB。

信号的反演带宽与设定条件的误差不超过0.4%，中心频点与设定条件的误差不超过0.3%，功率与设定条件的误差不超过2%。

3.2 注入式仿真条件及反演

仿真条件:发射信号为一个信号，发射信号中心频点500MHz，功率-40dBm。反演结果如图4 所示。

图3 数字仿真条件下反演得到的信号频谱、小波变换及信号奇异性图Fig.3 Signal spectrum，wavelet transform and signal singularity map obtained by inversion under digital simulation conditions

反演解算得到的信号频谱特征为:发射信号的反演带宽15kHz，中心频点100MHz，功率为-39.410 9dBm。发射信号的反演带宽与某商用检测软件显示带宽值17kHz 的差值为2kHz，中心频点与设定条件值相同，功率与设定条件的差值为0.589 1dB。

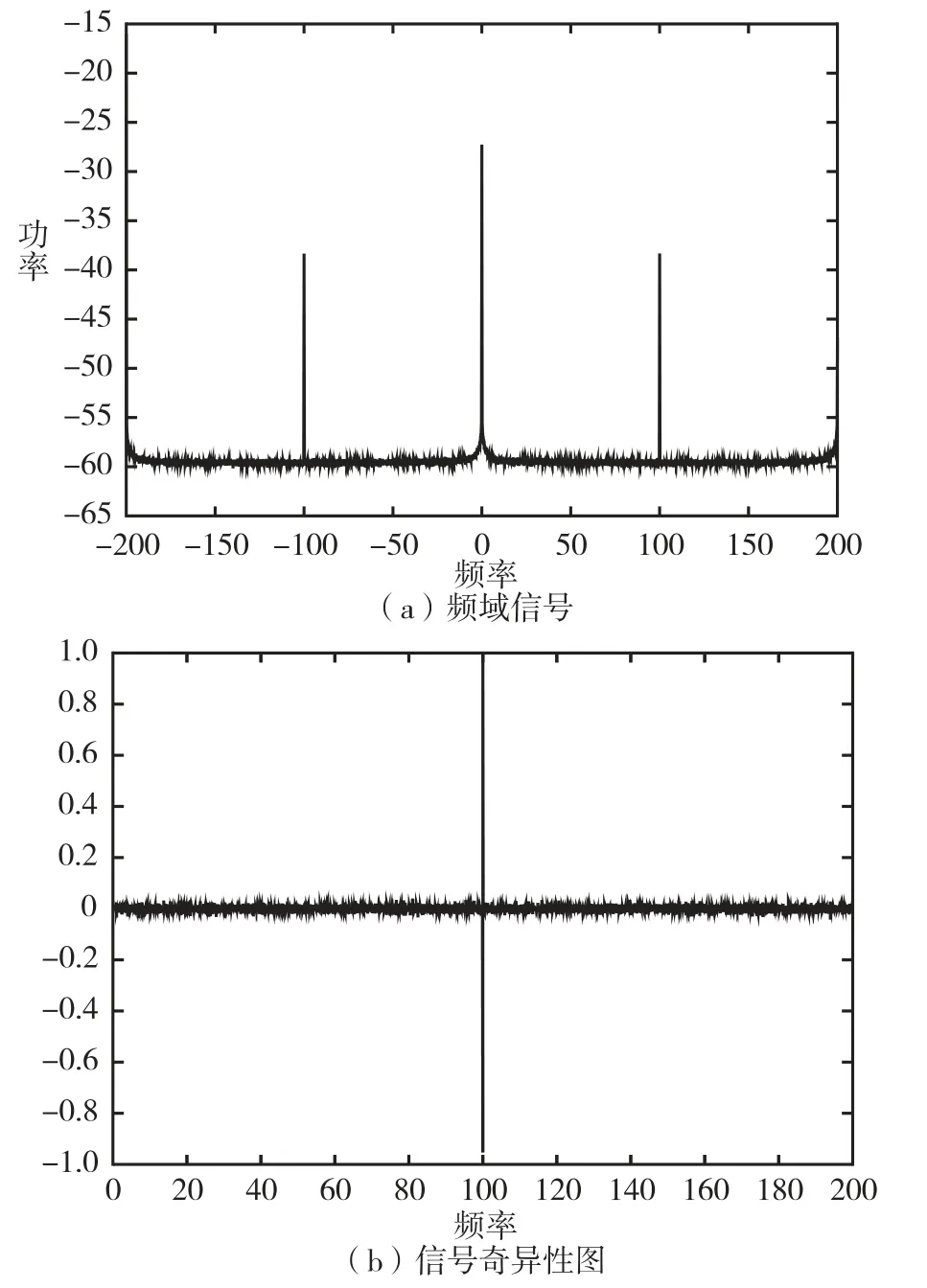
图4 注入式仿真条件下反演得到的信号频谱及信号奇异性图Fig.4 Signal spectrum and signal singularity map obtained by inversion under injection simulation conditions

信号的反演带宽与设定条件的误差不超过0.4%，中心频点与设定条件的误差不超过0.3%，功率与设定条件的误差不超过2%。

3.3 辐射式仿真条件及反演

仿真条件:发射信号为两个信号，发射信号①中心频点2 000MHz，功率10dBm；发射信号②中心频点2 001MHz，功率10dBm。反演结果如图5 所示。

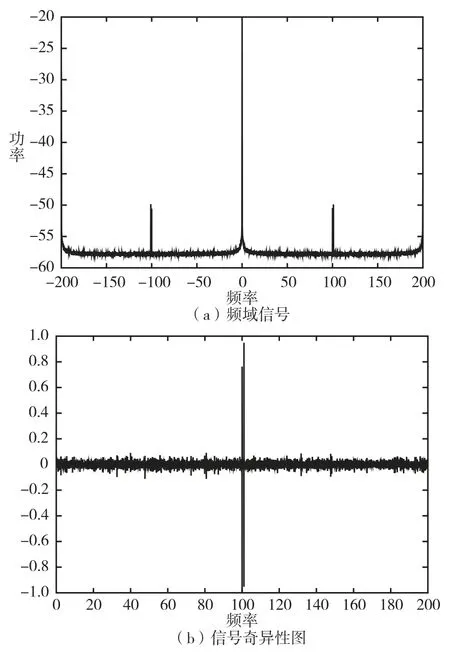
图5 辐射式仿真条件下反演得到的信号频谱及信号奇异性图Fig.5 Signal spectrum and signal singularity map obtained by inversion under the condition of radial simulation

反演解算得到的信号频谱特征为:发射信号①的反演带宽11kHz，中心频点100.002 0MHz，功率-50.768 0dBm；发射信号②的反演带宽11kHz，中心频点为100.001 0MHz，功率为-48.639 5dBm。发射信号①的反演带宽与某商用检测软件显示带宽值9kHz 的差值为2kHz，中心频点与设定条件的差值为0.002 0MHz；发射信号②的反演带宽与某商用检测软件显示带宽值9KHz 的差值为2kHz，中心频点与设置条件的差值为0.001 0MHz。

反演处理得到的电磁信号的带宽与某商用检测软件的显示结果接近，中心频点与设定条件的误差不超过0.1%。

4 结束语

本文提出的对无人机复杂电磁环境频谱特征反演测量的方法，该方法基于小波变换原理对无人机典型用频频段电磁信号进行变换处理，对其频谱特征进行奇异性检测，结合信号降噪处理去除频谱伪奇异点等对接收信号频谱特征进行反演测量，仿真结果的精度都达到对无人机典型用频频段选择的要求。