eLoran系统ASF网格应用算法研究
李 云 华 宇 燕保荣 郭 伟
(1.中国科学院国家授时中心,陕西西安710600;2.中国科学院大学,北京100049)
1 引 言
2018年,美国总统特朗普签署了《国家安全与弹性授时法案》。该法案要求交通部在两年内建设针对GPS 的地基备用授时系统。这在一定程度上宣布了美国的重启罗兰计划,同时提高罗兰系统的精度使其与GPS 系统相当。继BPL 和长河二号系统的eLoran 升级改造之后,我国也开展了高精度地基授时方面的研究,计划扩建eLoran 发播台满足eLoran 信号的全国土覆盖,同时要提高eLoran 系统的精度。
国内外专家对ASF 网格进行了一系列研究。2005年,Gregory William Johnson 等人通过大量测试数据分析二次时延的空间、时间和方向变化[3]。2012年,Hargreaves C 等人提出收集足够测量数据做出高精度ASF 数据库,能保证在海上定位结果优于10m(95%)[4]。还有专家学者从节省ASF 网格数据库的成本出发,分析用静态数据和动态数据建立ASF 网格两种不同的方法[5~8]。
有了ASF 数据库,用户确立所在网格根据内插算法解算出ASF 值,修正信号传播时延,从而提高授时精度。在ASF 数据库既定的情况下,内插算法本身也会引入新的误差,本文仿真分析不同空间插值算法带来的误差,并对算法进行比较,得出双线性插值算法误差最小,反距离插值算法误差最大。
2 eLoran 信号传播时延
eLoran 信号从发射天线到接收天线所经历的时间称为传播时延Tp,如式(1)所示。假设信号在无限大空气介质中传播时,由发射天线到接收天线所经历的时间称为一次时延(Primary Factor,PF),又称为基本时延;当信号在海平面传播时,传播时延与一次时延之差,称为二次时延(Secondary Factor,SF)反映了海平面对传播时延的影响;当信号在地平面传播时,传播时延与一次时延之差称为附加二次时延(Added Secondary Factor,ASF)反映了地平面对传播时延的影响[9]。

一次时延PF 计算公式如式(2)所示[10]

式中:C——真空中的光速,通常C=0.299 792 458km/μs;d——信号传播的大地线距离;ns——地面的大气折射指数,国际标准大气值ns=1.000 315。
二次时延SF/附加二次时延ASF 的计算公式如式(3)所示
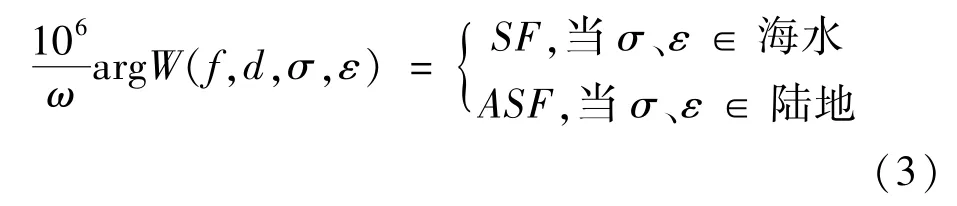
式中:ω——角速度,单位rad/s;W——衰减函数,与信号传播距离、传播路径介质的电导率、介电常数有关;argW——地波衰减函数W 的相位,单位rad;f——载波信号的频率,100kHz;d——信号传播的大圆距离,单位km;σ——信号传播路径上介质的电导率;ε——信号传播路径上的介电常数。
3 空间插值算法
常用的空间插值算法,包括双线性插值算法、反距离权值算法IDW(Inverse Distance Weighted,IDW)、Junkins 算法和自然邻域插值算法等。这里重点对双线性插值算法、反距离权值算法IDW、Junkins 算法进行仿真分析。
3.1 双线性插值算法
双线性插值算法是在x,y两个方向分别进行一次线性插值,如图1 所示。先x方向,后y方向插值,与先y方向,后在x方向插值,插值效果相同,其结果与插值顺序无关[11]。
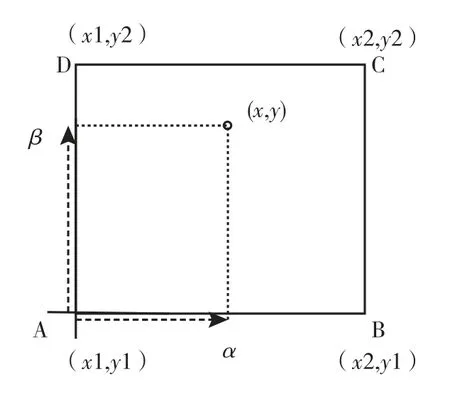
图1 双线性插值算法示意图Fig.1 Bilinear interolation algorithm
四个顶点的坐标分别为(x1,y1),(x2,y2),(x3,y3),(x4,y4),其ASF 分别为C1,C2,C3 和C4,待插值点(x,y)的ASF 如式(4)所示
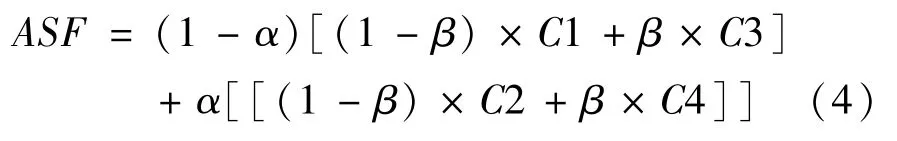
其中,
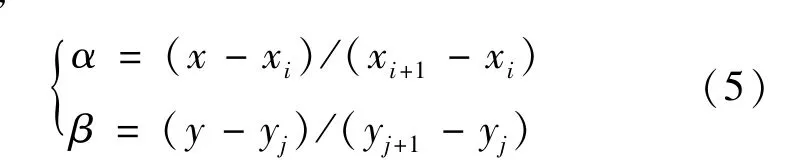
3.2 反距离插值
反距离权重IDW 插值使用一组采样点属性的线性权重组合来确定待插值点的属性,权重是一种反距离函数。这里反距离函数的幂值,取值为2。幂参数越高,可进一步强调最近点对插值点的影响,因此,邻近数据将受到更大影响,拟合的表面更加详细(更不光滑),内插值更接近相邻采样点的值。反之,幂参数越小,更远距离的采样点对插值点的影响越大,拟合的表面更光滑。
IDW 插值方法假定每个输入点都有着局部影响,这种影响随着距离的增加而减弱。算法描述:现有n个离散点Z(x1,y1),Z(x2,y2)…Z(xn,yn),需要对插值点(x,y)进行插值预测,求出Z(x,y),过程如下。
1)利用距离函数求出各离散点与插值点的距离,这里采用欧氏距离如式(5)所示
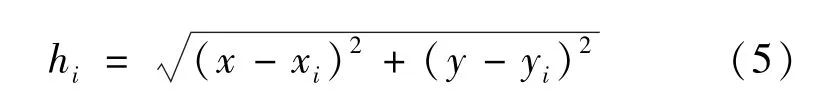
式中:(x,y)——插值点坐标;(xi,yi)——已知点坐标。
2)在幂参数确定的情况下,利用权重函数计算各个离散点的权重如式(6)所示
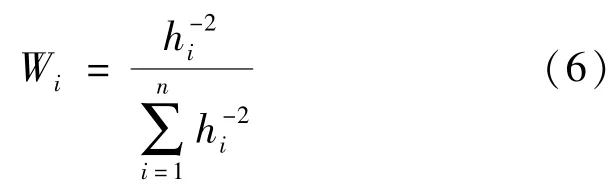
式中:n——离散点个数。
3)计算插值点的插值如式(7)所示
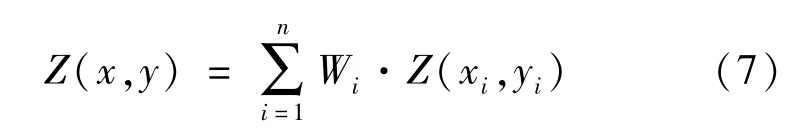
式中:Wi——第i采样点的权重;Z(xi,yi)——第i点的属性值。
3.3 Junkins 权值算法
Junkins 加权法是GPS 系统中用户穿刺点电离层垂直延迟的计算方法。Junkins 加权法与反距离插值算法相比,计算量较小,与简单的双线性加权法相比,其空间相关性较强[12],如图2 所示。其中,1~4 分别指网格结点,其对应的ASF 值分别为ASF1~ASF4;A 点为要拟合的点,其ASF 用ASF(φA,λA)表示为
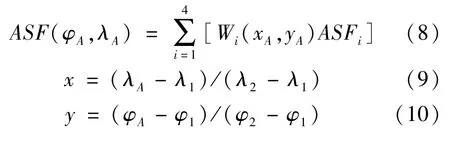
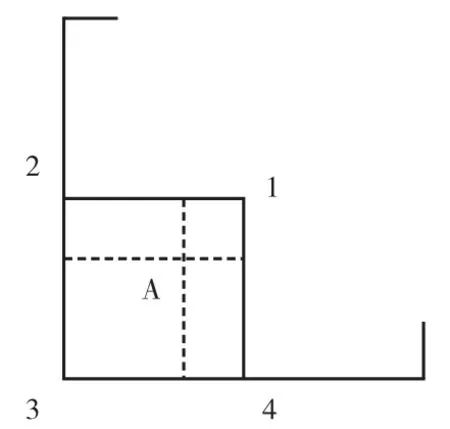
图2 Junkins 加权算法示意图Fig.2 The Junkins weighting method
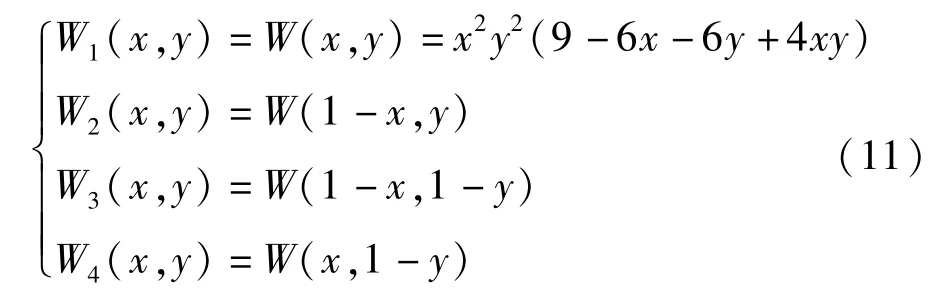
式中:W(x,y)——内插的加权函数。
4 算法仿真分析
4.1 双线性插值算法仿真
4.1.1 不同的网格大小
双线性插值算法在不同大小网格内的插值误差分析如图3 所示,从上到下依次是网格大小为0.5°,0.2°和0.1°,信号传播路路径是平均陆地电导率σ=0.003,ε=22 误差范围分别为(0~6)ns,(0~1)ns 和(0~0.2)ns,显然网格越小,ASF 网格的精度越高。误差最小的区域分布在网格的四个顶点附近,误差最大的区域集中在网格的中心部位。因此相对来说离网格顶点越近,误差越小,距离网格顶点越远误差越大;距离网格中心越近误差越大,距离网格中心越远,误差越小。
4.1.2 不同的传输路径
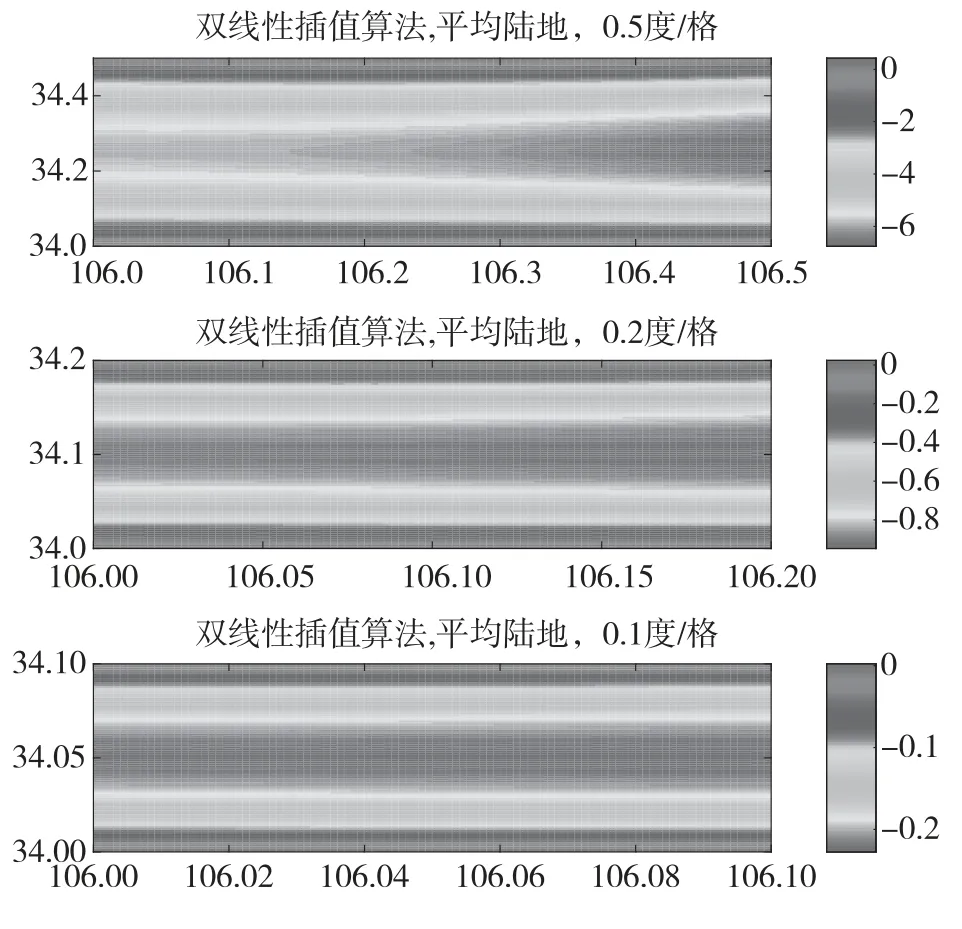
图3 双线性插值算法(不同的网格大小)Fig.3 The bilinear interpolation algorithm (different mesh sizes)
双线性插值算法应用在海水路径、平均陆地和甚干燥地路径三种路径上的0.1°网格中的插值结果的误差如图4 所示。海水介质的误差范围在(0~0.1)ns 左右,平均陆地和甚干燥地在(0~0.2)ns 左右。随着路径的电导率变小,路径的传输介质对信号的阻力增强,同时ASF 网格的误差也变大。因此海水路径对信号的阻力最小,ASF 值最小,相应的ASF 网格计算的误差最小;随着信号传输路径上介质对信号的阻力逐渐变大,ASF 值变大,相应的ASF 网格计算结果的误差逐渐变大。从网格中心处向外部误差逐渐变小,呈现处出一定的层次感。
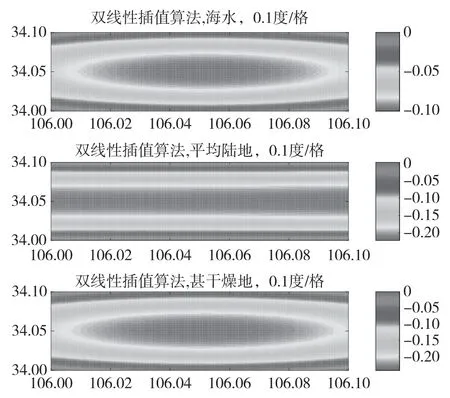
图4 双线性插值算法(不同传输路径)Fig.4 The bilinear interpolation algorithm (different path)
4.2 反距离插值算法仿真
4.2.1 不同的网格大小
对反距离权值算法的仿真如图5 所示,从上到下依次是网格大小为0.5°,0.2°和0.1°,误差范围分别为(0~40)ns,(0~15)ns 和(0~8)ns。显然网格越小,ASF 网格能实现的精度越高。IDW 算法网格误差分布较分散,网格中靠近顶点的分散区域误差最小,同时网格的中心部分误差最小,误差最大的区域包括网格的侧边的几个分散区域。
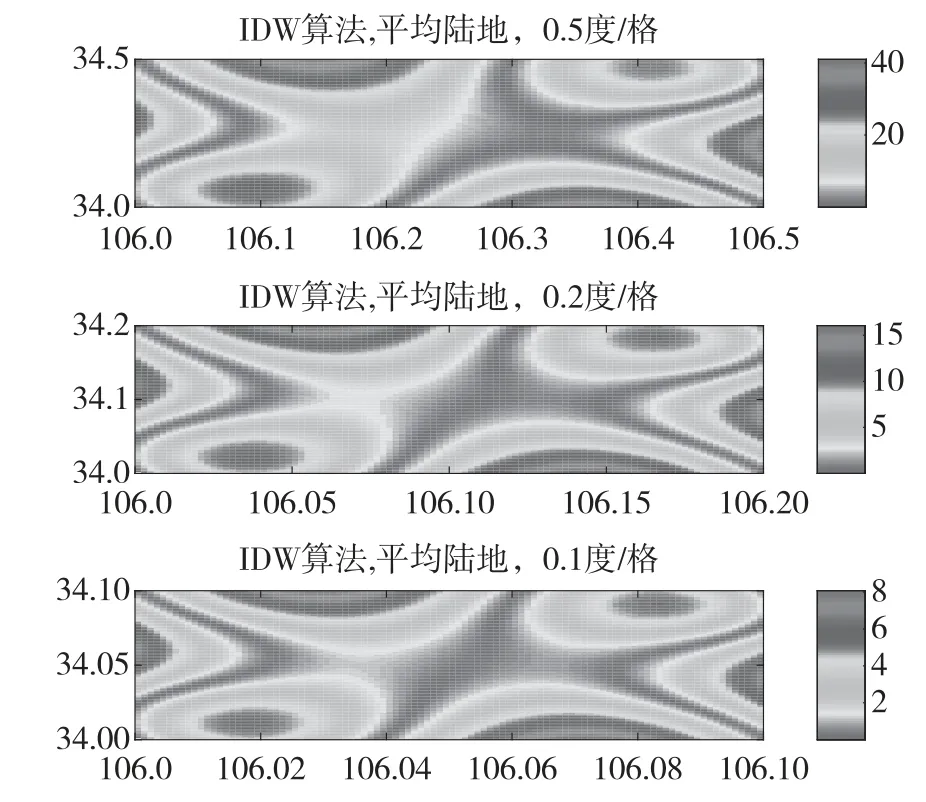
图5 反距离加权插值算法(不同网格大小)Fig.5 IDW interpolation algorithm (different mesh sizes)
4.2.2 不同的传输路径
针对海水路径、平均陆地和甚干燥地三种路径上,网格大小0.1°时的误差情况如图6 所示。不同的信号传输路径ASF 网格内插结果的误差:海水介质的误差范围在(0~2.5)ns,平均陆地的误差范围在(0~6)ns 和甚干燥地的误差范围在(0~8)ns。从甚干燥地到海水随着路径的电导率变小,路径的传输介质对信号的阻力减小,同时ASF 网格的误差也变小。因此甚干燥地路径对信号的阻力最大,相应的ASF网格计算的误差最大,随着信号传输路径上介质对信号的阻力逐渐变小,ASF 网格计算的误差逐渐变小。
4.3 Junkins 插值算法仿真
4.3.1 不同的网格大小
junkins 算法的结果误差分析如图7 所示,从上到下依次是网格大小为0.5°,0.2°和0.1°,误差范围分别为( -20~20)ns,( -10~10)ns 和( -5~5)ns,网格越小,ASF 网格能实现的精度越高。误差分布的规律性介于双线性插值差算法和反距离插值算法之间,网格内左下角部分网格误差小,右上角区域网格误差大,误差的分布较集中。

图6 反距离加权插值算法(不同传输路径)Fig.6 IDW interpolation algorithm (different path)
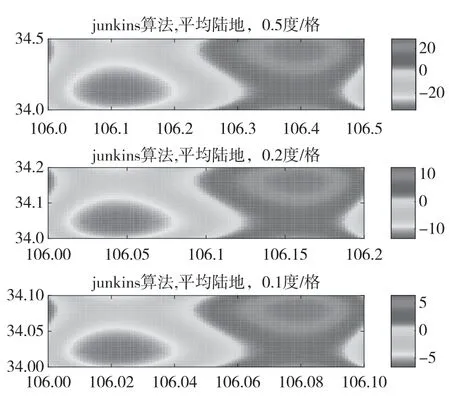
图7 Junkins 算法(不同网格大小)Fig.7 The junkins weighting method(different mesh size)
4.3.2 不同的传输路径
按照网格0.1°时计算的海水路径、平均陆地和甚干燥地路径的误差情况如图8 所示,海水介质的误差范围在( -2 ~2)ns,平均陆地的误差范围在( -5~5)ns和甚干燥地的误差范围在( -5~5)ns。随着路径的电导率变小,路径的传输介质对信号的阻力增强,同时ASF 网格的误差也变大。因此,海水路径对信号的阻力最小,相应的ASF 网格计算误差最小,随着信号传输路径上介质对信号的阻力逐渐变大,ASF 网格的计算误差逐渐变大。
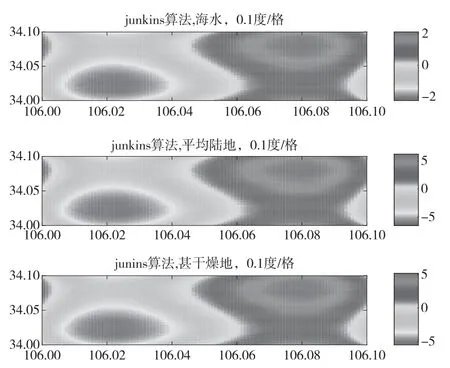
图8 Junkins 算法(不同传输路径)Fig.8 The Junkins weighting method(different path)
5 算法比较
首先在待测试区域建立4 个网格,每个网格经纬度方向的大小0.2°,待测试区域到发播台的信号传输路径属于平均陆地。比较三种网格应用算法如图9 所示,从上到小依次是IDW 插值算法、Junkins 插值算法和Bilinear 插值算法,从最左边一列看出三种算法误差分布IDW 插值算法误差分布的规律性最差,误差最小的区域集中在网格中心部位,误差大的区域分散在网格的边缘区域;Junkins 算法的规律性介于二者中间,误差最小的区域集中在网格的左下部分,误差大的区域集中在网格的右上部分;双线性算法误差分布的规律性最好:离网格顶点越近,误差越小,离网格顶点越远,误差越大,从网格中心向外部扩散开来误差逐渐变小。
图9 中间一列是色柱,反距离插值算法的误差范围是(0~15)ns;Junkins 算法的误差范围是( -10 ~10)ns;双线性插值算法的误差范围是(0~1)ns,双线性插值算法引入的误差最大。
图9 中,右侧3 个图分别是三种算法的误差概率分布函数曲线图。IDW 插值算法误差不大于20ns,95%的误差小于12ns,Junkins 插值算法误差不大于15ns;95%的误差小于10.7ns,Bilinear 插值算法误差不大于1.2ns,95%的误差小于0.9943ns。三种算法分析比较得出IDW 插值算法误差最大,Junkins 算法误差次之,双线性插值算法的误差最小。
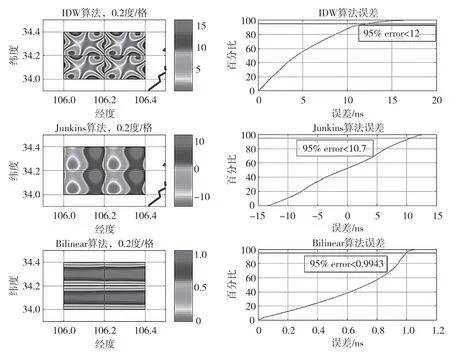
图9 三种插值算法的比较示意图Fig.9 The comparison of three interpolation algorithms
6 结束语
通过以上仿真分析比较,双线性插值算法的误差最小,而且呈现一定的规律型从网格中心到网格边缘误差逐渐减小;反距离插值算法优于要计算距离算法计算量最大,误差最大,而且误差的规律性差;Junins 算法计算量、误差大小以及误差的规律性在三种算法中居中。

