基于遗传算法的阵列天线波束能量定量控制技术

王友保，王英植，张宥诚

(南京信息工程大学 应用电磁学研究中心，江苏 南京 210044)

在移动通信领域，随着移动用户数据业务的增加，通信系统能耗不断提高，因此降低系统能耗已成为移动通信要解决的问题.目前，无论用户是否需要信号，大部分发射天线(如无线局域网天线、基站天线等)均处于全天候满负荷状态，能量浪费严重.随着第5代移动通信技术的兴起，大规模多输入多输出(multiple input and multiple output， 简称MIMO)将成为下一代无线网络的关键技术，基站大规模MIMO天线的应用将使能耗更大.因此，解决天线系统能耗问题对提高能源利用率，具有重要意义.为此，国内外学者做了大量研究.在提高微波能量转换效率方面，文献[4]分别从发射天线和接收天线的角度，提出了两种用来提高能量传输转换效率的方法，但是这两种方法对天线有较高要求.在微波输能领域，文献[5]利用场积分得到适用于任意平面阵列天线的波束能量传输效率最大化的一般表达式，并对结果进行仿真验证，然而验证过程复杂.相比之下，文献[6]提出了一种保证阵列天线能量传输效率最大化方法，此方法操作简单，可应用于聚焦阵列天线、无线输能阵列天线.在文献[6]的基础上，文献[9]提出了有约束条件的阵列天线激励优化方法，实现了阵列天线近场平顶波束赋形.此外，遗传算法和粒子群算法，已广泛应用于阵列天线激励寻优.上述文献在一定程度上实现了微波能量的有效利用，但均不能从定量角度实现微波能量的有效利用，而波束能量的定量控制才是微波能量有效利用的关键.

该文将微波网络能量传输最优理论与遗传算法相结合，提出阵列天线波束能量的定量控制技术.首先，将给定的发射阵列天线和若干接收天线看成一个微波网络，并通过HFSS仿真得到该微波网络的散射矩阵；其次，根据接收天线反射波与发射天线入射波间的关系，构建微波网络能量传输效率最大化的约束条件；再次，用遗传算法优化得到发射阵列天线的最优端口激励分布；最后，在HFSS中基于优化的激励分布给阵列天线馈电，得到阵列天线的远场电场分布.仿真验证表明该技术能对阵列天线的波束能量进行定量控制.

1 波束能量定量控制的遗传算法

1.1 波束能量定量控制的数学描述

设发射天线个数为

n

，接收天线个数为

m

，则发射天线及接收天线构成一个

n

+

m

端口的微波网络系统，如图1所示.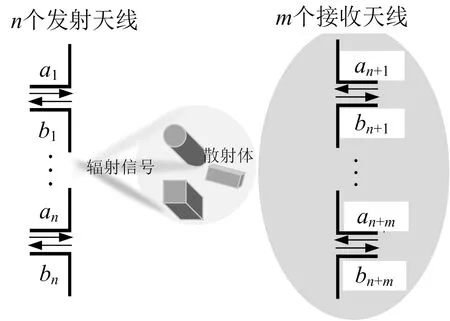

图1 n+m端口微波网络系统

通过散射矩阵将各端口入射波组成的矢量与反射波组成的矢量联系起来，如下式

(1)

其中：下标t表示发射天线，下标r表示接收天线；=[

a

a

,…,

a

]为发射天线的入射波，为接收天线的入射波；为发射天线的反射波，=[

b

+1

b

+2,…,

b

+]为接收天线的反射波；，，，为散射矩阵的子矩阵.设

T

为发射天线与接收天线间的功率传输效率，由文献[6]可知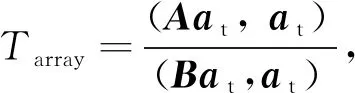

(2)

=.

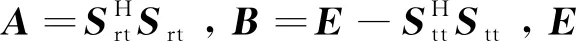
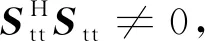
(3)

对进行设定后，便可确定发射天线的波束能量.于是，待解决的问题就是：求解，使其满足(3)式，同时保证(2)式的值最大.这样，天线波束能量定量控制问题就转化为求解有约束条件的极大值问题，即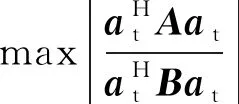

使得

=.

(4)

1.2 遗传算法目标函数的构建

将(4)式中的最大值函数

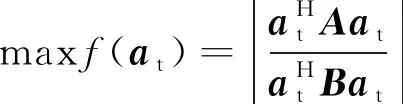
(5)

作为遗传算法的第1目标函数.将式(4)中的约束条件变为-=0.由于遗传算法仅能对实数求解，故将其转化为|-|>=0.构建第2目标函数为min

f

()=|-|>.

(6)

1.3 遗传算法适应度函数的设计

在实际应用中，适应度函数是遗传算法的关键.构建适应度函数方法有：搜索空间限定法、可行解变换法和罚函数法.该文波束能量定量控制问题采用罚函数法.设计的适应度函数为

(7)

其中：

β

，

δ

为根据经验设定的常数，通常情况下

β

=2,

δ

的表达式为

δ

=-10(1-)，

(8)

其中：

ρ

为可行解比例，

α

为1～10的自然数.根据目标函数的处理结果，可得适应度函数为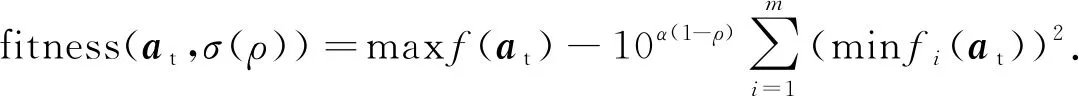

(9)

1.4 定量控制问题的算法实现

1.4.1 编码设计

遗传算法的基因编码采用二进制，最小编码长度的确定方法来源于文献[22]，其计算公式为

k

=log(

b

-

a

)+

c

log10，

(10)

其中：

k

为中间变量，(

b

-

a

)为决策变量的可行区间，

c

为小数点后的位数，

l

为编码长度.决策变量=[

a

,

a

,…,

a

]为天线的端口激励，由于其为矢量组成的矩阵，因此要对中各矢量的实部和虚部分别进行二进制编码.编码过程要产生1组随机编码解

P

(

t

),

t

∈{1,2,…,2

n

}.每个初始染色体包含2

n

列元素，其中奇数列元素为天线阵元端口激励实部的二进制编码序列，偶数列元素为天线阵元端口激励虚部的二进制编码序列.遗传算法基因型到表现型的映射关系为[

P

(1)]+i[

P

(2)]→

a

，[

P

(3)]+i[

P

(4)]→

a

，

⋮

[

P

(2

n

-1)]+i[

P

(2

n

)]→

a

，

(11)

其中：下标10表示十进制，i为虚数单位.

定义种群实部的可行域为[-

R

,

R

]，虚部的可行域为[-

I

,

I

].仿真计算发现，要保证波束能量定量求解的准确性，可行域的边界应满足3

b

≤{

R

,

I

}≤5

b

，其中

b

为各分量绝对值的最大值.

1.4.2 遗传操作

遗传算法的运行机制来自两个生物学原理，即“自然选择”和“自然遗传”.遗传算法的3个基本操作为：选择(selection)、交叉(crossover)和变异(mutation).该文遗传算法有关设置如下：种群规模POP=100，最大遗传代数MAXGEN=300；选择方式采用随机遍历抽样；交叉方式采用单点交叉，交叉概率CROSS=0.7；基因变异概率MUTATION=0.01.

2 阵列天线设计

将微带单极子天线作为天线阵元，单极子的中心频率为2.45 GHz，馈电方式为同轴馈电.天线基板采用环氧树脂FR4材质，其介电常数为4.4，介电损耗角正切大小为0.02.用上述单极子天线组成8单元阵列天线，如图2所示.天线端口号与阵元编号一致，天线的具体参数如下：

L

=62 mm，

W

=62 mm，

L

=26 mm，

W

=29 mm，

d

=6 mm，

d

=3 mm，

d

=10 mm，

h

=4 mm.由于阵列天线各阵元呈左右对称分布，因此图3中仅给出端口1，2，5，6的反射系数.由图3可知，阵列天线各单元均在2.45 GHz频点附近匹配.

图2 单极子阵元和阵列天线的几何结构 图3 阵列天线端口1，2，5，6的反射系数

3 定量控制效果验证

3.1 阵列天线端口激励获取流程

在HFSS中阵列天线端口激励分布的获取流程如图4所示.

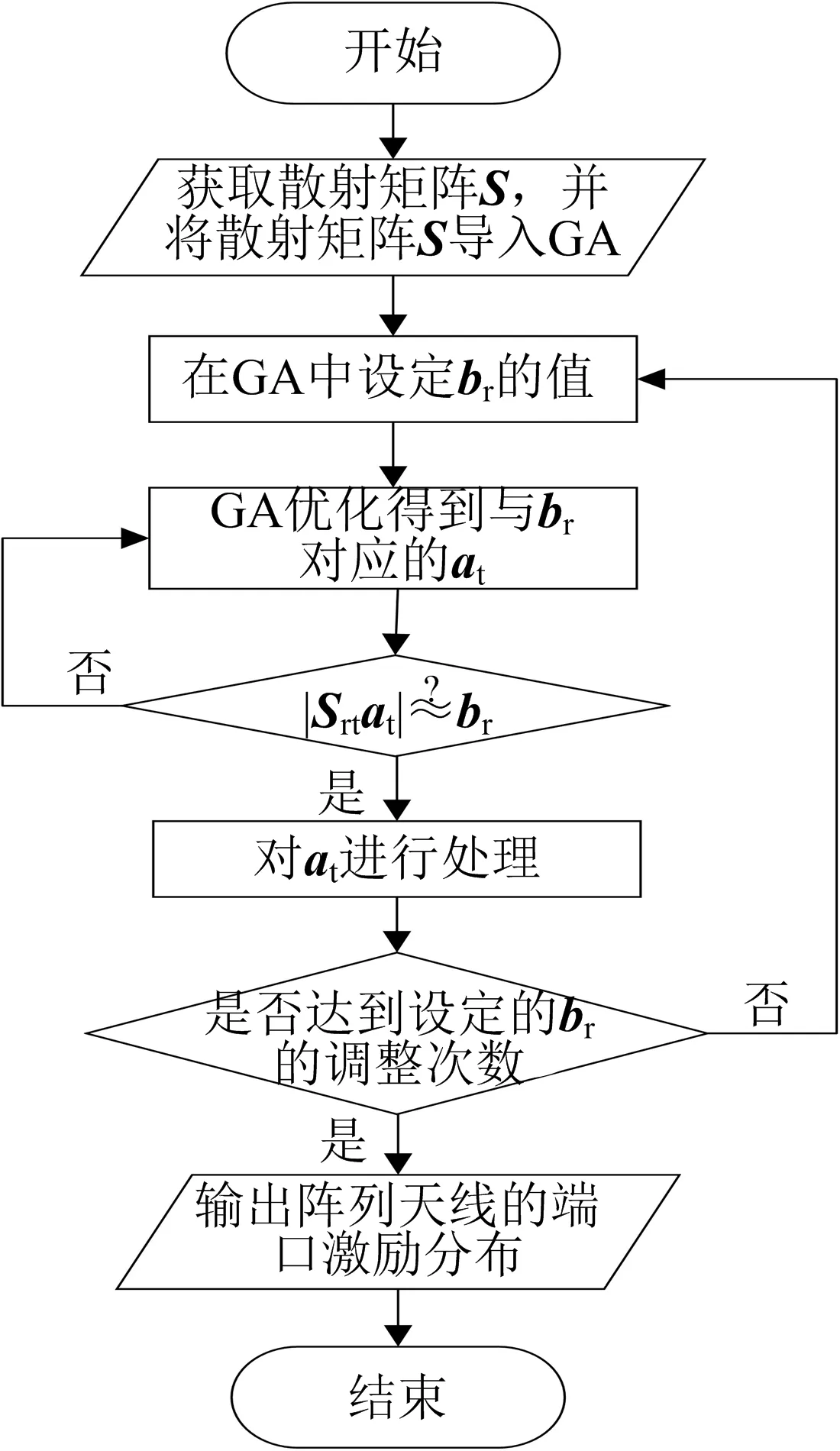
图4 阵列天线端口激励分布的获取流程

阵列天线端口激励分布获取的步骤为：

(1) 在HFSS中，设计微波网络模型，得到微波网络的散射矩阵，且将导入遗传算法;(2) 在算法中，设定的值，优化得到与之对应的;(3) 将||>与||>进行对比，若不满足||>≈||，则重新运行遗传算法，若满足||>≈||，则通过abs()及angle()×180/π分别得到阵列天线端口激励的幅值及相位;(4) 调整的值多次，获取多种定量情况下的.

3.2 微波网络系统设计与仿真验证

3.2.1 8+1端口微波网络系统

对于8+1端口微波网络系统，接收天线为1个单极子天线，置于

Z

轴上方，其辐射贴片位于坐标原点正上方1.196 m的远场区域，如图5所示.

图5 8+1端口微波网络系统示意图

设接收天线在1.196 m处的有效长度为

L

、电场强度幅值为||、信号强度为

U

，则有

U

=||·

L

.当接收天线个数为1时，||=

b

，定量控制满足

b

≈

U

.表1列举了5种定量情况的设置.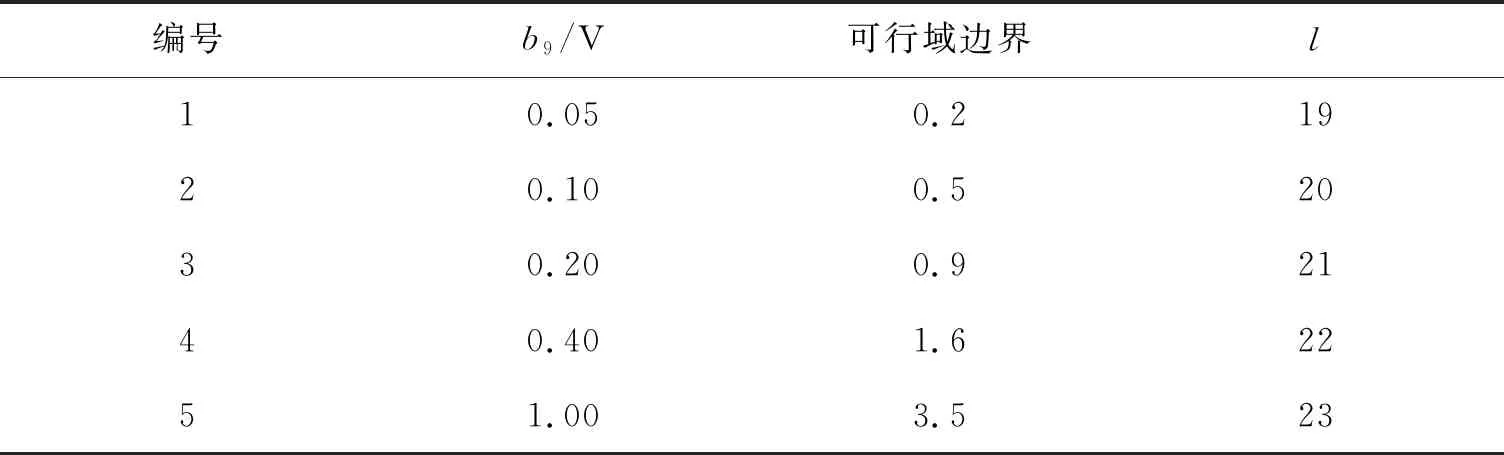

表1 8+1端口微波网络系统的5种定量情况的设置

5种定量情况下遗传算法适应度函数值的变化情况如图6所示.从图6可看出，5条适应度函数曲线均收敛，表明该文设计的适应度函数是合适的，优化得到的能使能量传输效率最大.

图6 8+1端口微波网络系统的5种定量情况下适应度函数值

图7给出了5种定量情况下阵列天线

YOZ

平面远场总电场信号强度.由图7可知，5种定量情况下最大远场总电场均在

θ

=0°处，且与接收天线所在方向一致.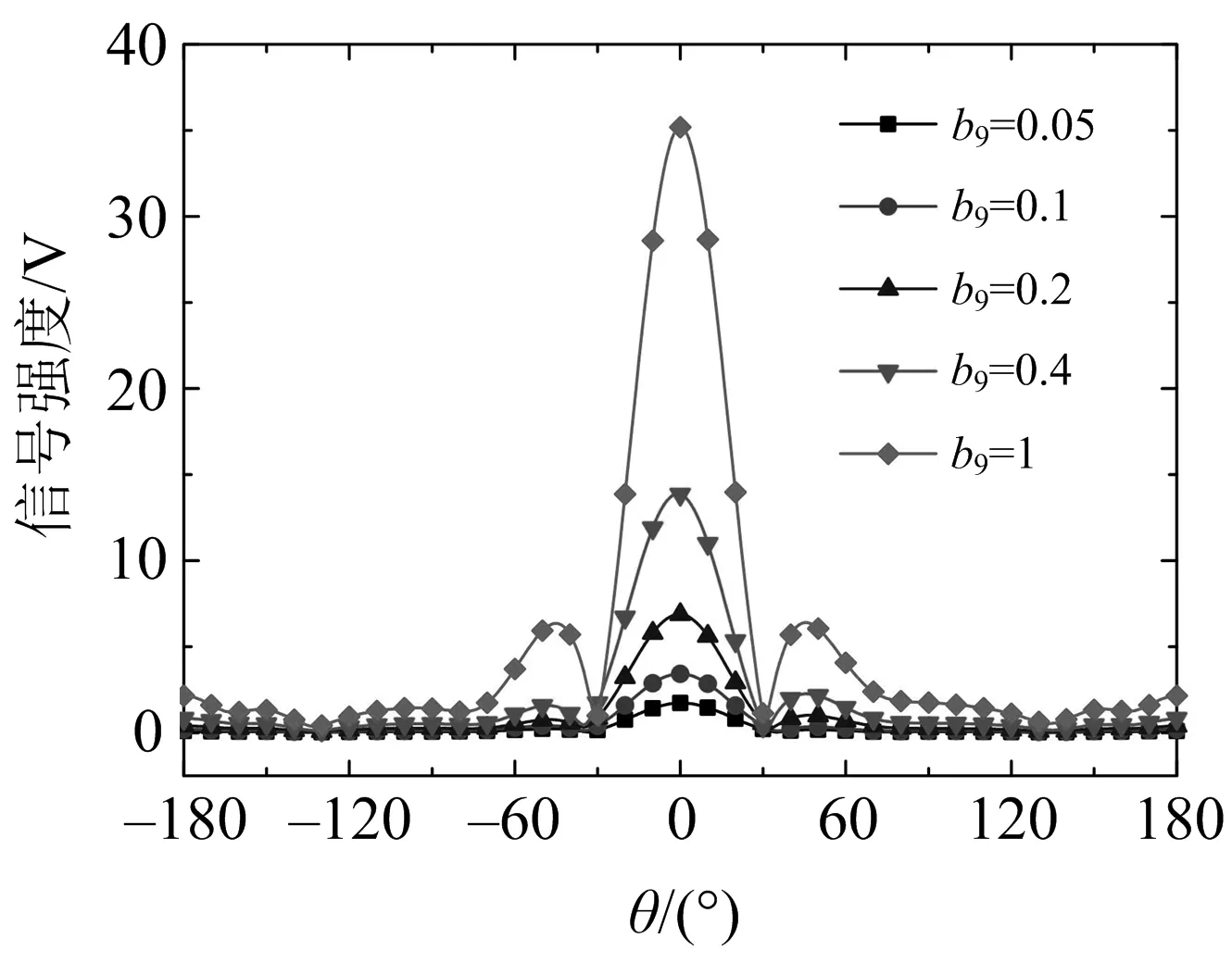

图7 8+1端口微波网络系统5种定量情况下阵列天线YOZ平面远场总电场信号强度

图8给出了HFSS中阵列天线沿

Z

轴的电场复振幅的分布情况，据此可得1.196 m处的电场强度幅值|

E

|.

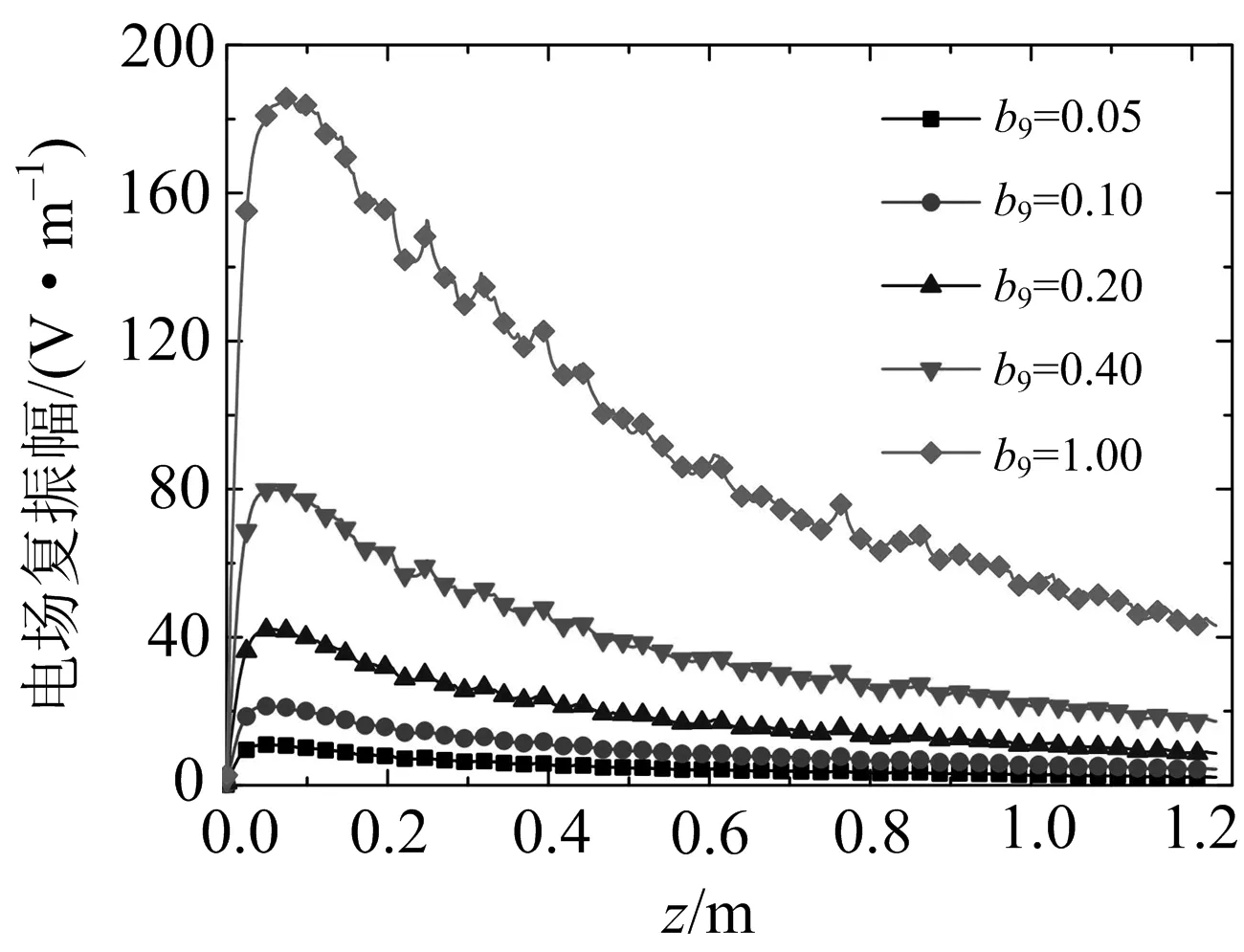
图8 8+1端口微波网络系统5种定量情况下阵列天线沿Z轴的电场复振幅

通过多种定量数据仿真，最终确定接收天线在1.196 m处的有效长度

L

=0.023 m.计算得到的5种定量情况下接收天线所在处的信号情况如表2所示.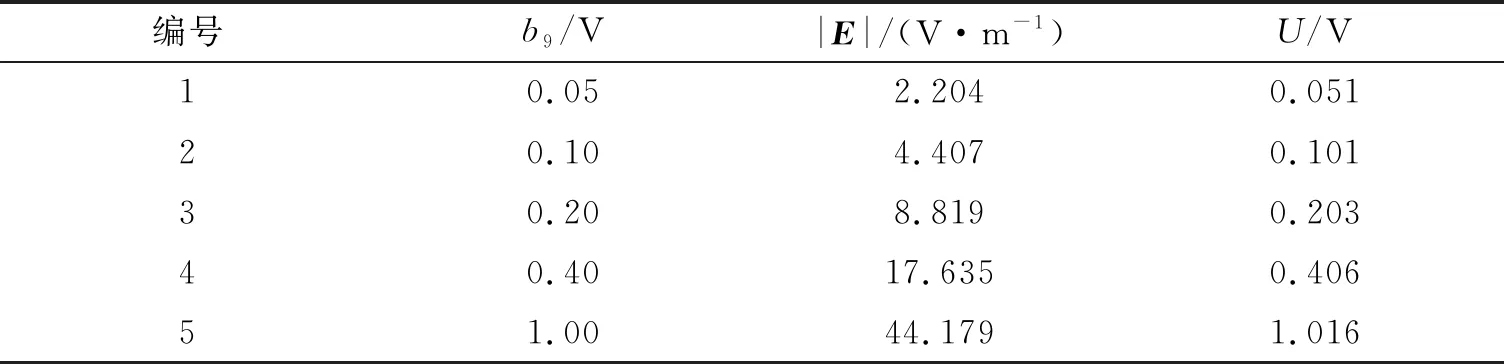

表2 8+1端口微波网络系统5种定量情况下接收天线所在处的信号情况

由表2可知，计算得到的5种定量情况下阵列天线所在处的信号强度

U

与设定值

b

基本吻合，表明该文的定量控制有效.表3给出了5种定量情况下阵列天线的端口激励分布.

表3 8+1端口微波网络系统5种定量情况下阵列天线的端口激励分布

由表3可知，同一端口5种定量情况幅值之比与设定值

b

之比吻合，且各端口的相位差异不大，表明该文的定量控制技术适用于8+1端口微波网络系统.

3.2.2 8+2端口微波网络系统

8+2端口微波网络系统的接收天线为2个单极子天线，接收天线1，2在

Y

轴正上方且与

Z

轴对称，两接收天线的金属贴片均位于坐标原点1.196 m的远场区域，如图9所示.

图9 8+2端口微波网络系统示意图

两接收天线的有效长度均为

L

，则接收天线1所在处的信号强度

U

=||·

L

，接收天线2所在处的信号强度

U

=||·

L

.当接收天线个数为2时，有=[

b

,

b

]，

b

和

b

分别对应接收天线1和接收天线2所在处的信号强度，定量控制满足|

b

|≈

U

，|

b

|≈

U

.8+2端口微波网络系统的5种定量情况的设置如表4所示.

表4 8+2端口微波网络系统5种定量情况的设置

图10为5种定量情况下遗传算法适应度函数值的变化情况.由图10可知，5条适应度函数曲线均收敛，表明设计的适应度函数具有合理性.

图10 8+2端口微波网络系统的5种定量情况下适应度函数值

图11给出了5种定量情况下阵列天线

YOZ

平面远场总电场信号强度.从图11可以看出，阵列天线在

θ

=±30°处的总电场信号强度随变化而出现较大波动.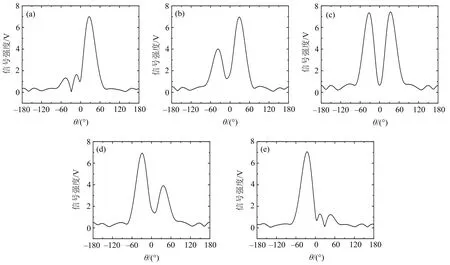

(a)b9=0,b10=0.2;(b)b9=0.1,b10=0.2;(c)b9=0.2,b10=0.2;(d)b9=0.2,b10=0.1;(e)b9=0.2,b10=0.图11 8+2端口微波网络系统的5种定量情况下的阵列天线YOZ平面远场总电场信号强度

图12给出了5种定量情况下阵列天线沿

θ

=±30°方向的电场复振幅，据此可得到两个接收天线1.196 m处的电场强度幅值.通过多种定量数据仿真，最终确定两接收天线1.196 m处的有效长度

L

=0.026 m.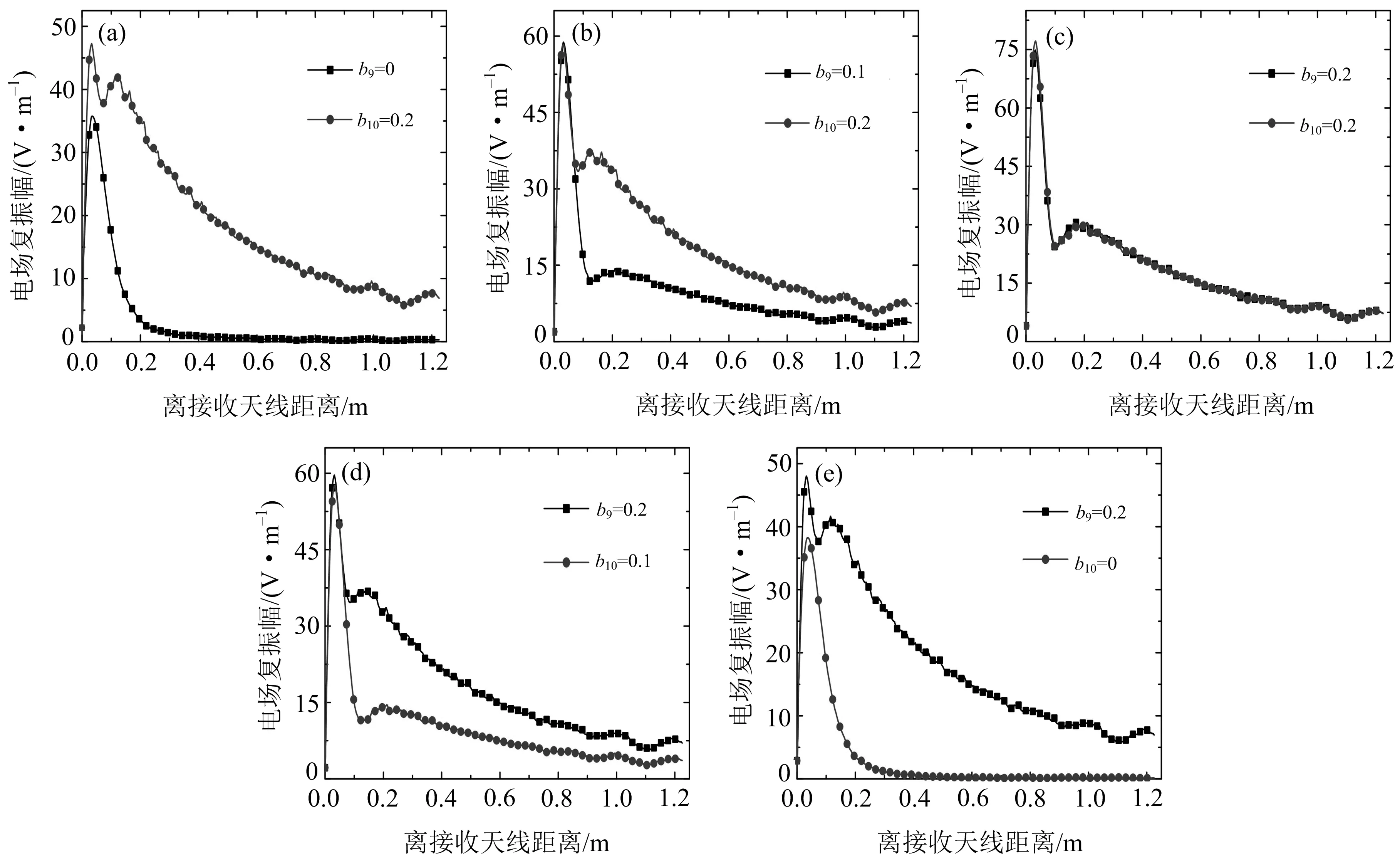

(a)b9=0,b10=0.2;(b)b9=0.1,b10=0.2;(c)b9=0.2,b10=0.2；(d)b9=0.2,b10=0.1；(e)b9=0.2,b10=0.图12 8+2端口微波网络系统5种定量情况下阵列天线沿θ=±30°方向的电场复振幅

计算得到的5种定量情况下两接收天线所在处的信号情况如表5所示.

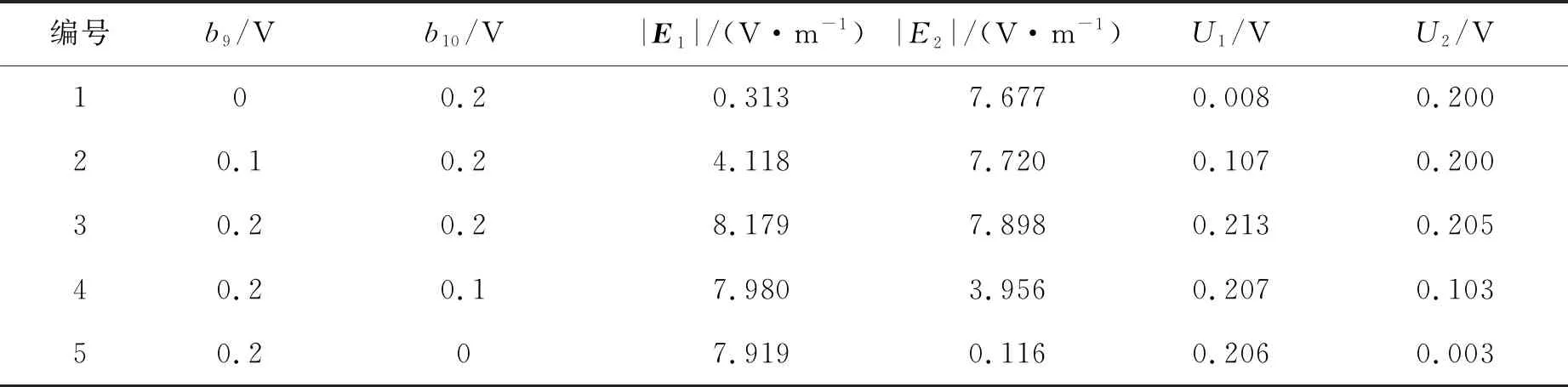
表5 8+2端口微波网络系统的5种定量情况下两接收天线所在处的信号情况

由表5可知，计算得到的阵列天线所在处的信号强度=[

U

,

U

]与设定值=[

b

,

b

]基本吻合，表明该文的定量控制对于8+2端口微波网络系统同样有效.

表6给出了5种定量情况下阵列天线的端口激励分布.

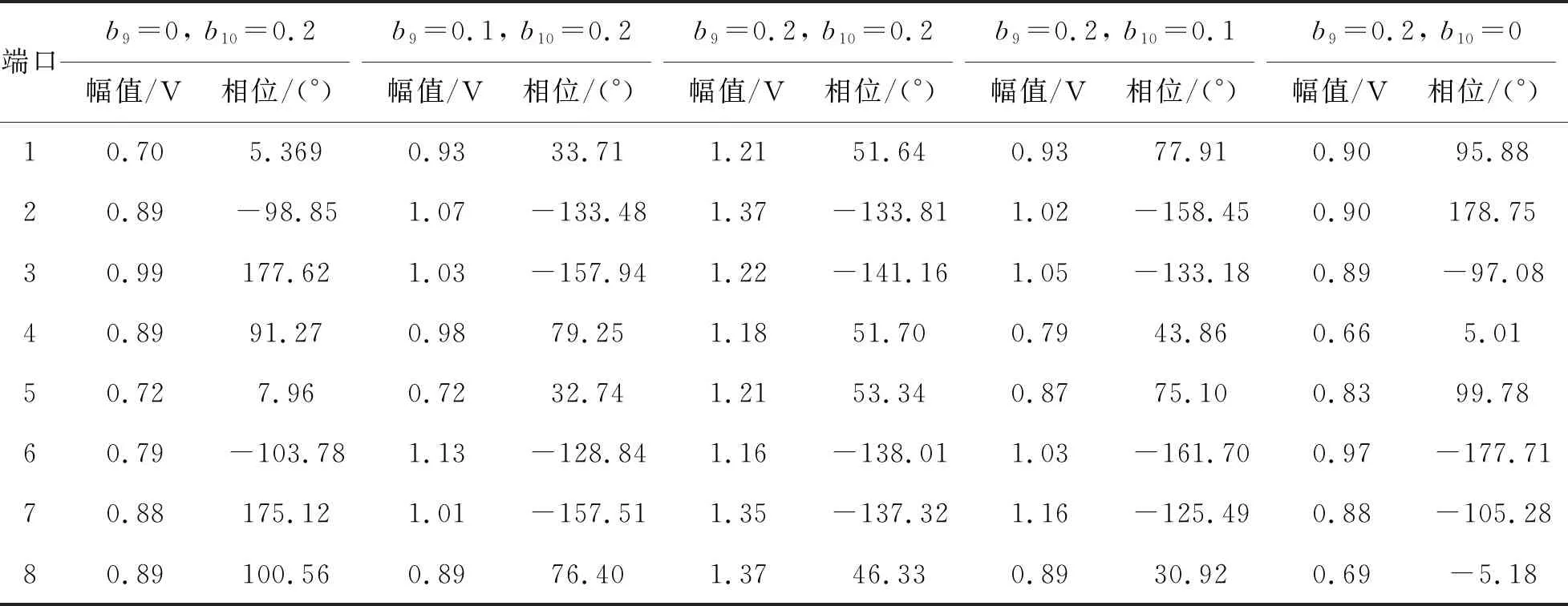
表6 8+2端口微波网络系统5种定量情况下的端口激励分布

由表6可知：各端口幅值随

b

和

b

变化而变化，当

b

=0.2，

b

=0.2时，幅值最大；随着接收天线数量、方位的改变，各端口相位也相应改变.可见，该文的定量控制技术同样适用于8+2端口微波网络系统.

4 结束语

该文将波束能量定量控制问题归结为含有约束条件的极值问题.为了实现对阵列天线波束能量的定量控制，在适应度函数的设计时引入了自适应罚函数，通过罚函数将定量约束问题转化为非约束问题.在遗传算法中，对接收天线处的信号强度进行设定，优化得到阵列天线端口激励分布.在HFSS中，根据||与接收天线有效长度

L

的乘积得到接收天线所在处的信号强度，且将信号强度与设定值进行对比.8+1，8+2端口微波网络系统的仿真验证结果表明：通过增大或减小的值，可调整阵列天线的信号辐射强度，进而定量控制不同接收天线所在区域的能量辐射.