基于相空间重构的电压暂降分类方法

程志友，臧世民

(1.安徽大学 教育部电能质量工程研究中心，安徽 合肥 230601;2.安徽大学 电子信息工程学院，安徽 合肥 230601)

太阳能及风能为主的DG(distributed generation)接入使电能质量问题变得十分复杂.电压暂降造成的经济损失约占全体电能质量扰动损失的80%，因此治理电压暂降就显得尤为重要.由于不同暂降类型对应不同治理方案，故必须首先对其进行分类.

自文献[7]基于电路系统提出将电压暂降造成的故障分成7类后，文献[8]对其进行补充，划分为9类，分别记为a～i.文献[9]采用对称分量分析法，对c，d类故障进行细分，然而其采用的故障特征量较多.文献[10]采用卷积神经网络与随机森林相结合的方法，对三相电压故障进行分类，但训练时间较长.文献[11]提出一种基于顺序选择的分类方法，计算流程较卷积神经网络方法有所简化，然而实现难度较大.文献[12]对三相电压信号进行Clarke变换，将三相电压信号正序、负序信息转换至

α

,

β

坐标系，且绘制出暂降椭圆图形，通过椭圆倾角完成分类.虽然该方法增强了分类的直观性，并实现了电压暂降的分类，但是其仅从单一特征入手，忽略了零序电压的存在，准确率不很高.为了解决分类速度欠佳、分类不直观的问题，文献[13]根据相空间重构图对电能质量进行分类，该方法规避了序列信息、较直观，然而并未获得轨迹所包含的暂降相位关系及幅值信息，故可能导致误判.

针对上述分类方法存在的复杂、实时性不强及误判等问题，该文提出基于相空间重构的电压暂降分类方法.对无扰动三相信号进行相空间轨迹变换，获得变换矩阵.对持续时间不足1周期的信号通过变换矩阵重构周期信号，对持续时间为1周期以上的信号使用变换矩阵进行处理.通过仿真实验及算例分析验证所提方法的可行性.

1 相空间重构

1.1 相空间轨迹

理想的电力系统是三相平衡且对称的，然而多种因素的影响使故障经常发生，现以一相电压为例进行说明.归一化后的电压信号可由下式表示

u

(

t

)=

A

(

t

)sin[

ωt

+

φ

(

t

)]，

(1)

其中：

A

(

t

)为电压振幅；

φ

(

t

)为初相位，表征发生电压暂降时伴随的相位跳变.离散化

u

(

t

)得到的电压时间序列为

u

,

u

,…，

u

，该序列对应的

m

维相空间为=[

u

,

u

+,…,

u

+(-1)]，

i

=1,2,…,

N

-(

m

-1)

τ

，其中：

τ

为延迟因子.第

j

相信号的相空间轨迹矩阵为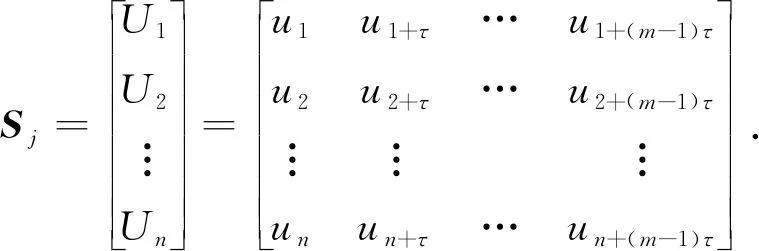

(2)

为避免采样频率变化导致的延迟因子不一致及端点效应的最小化，选取

τ

=1.根据Takens定理，为了保证相空间吸引子的拓扑特征不变，该吸引子的重构维数至少为原吸引子所处空间维数的2倍且加1.原吸引子维数为1，故重构维数

m

=3，则式(2)改写为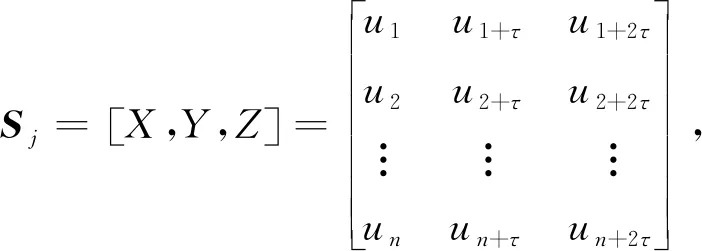

(3)

其中：

X

,

Y

,

Z

均为列向量.

1.2 相空间轨迹变换

为了获得电压暂降的相空间轨迹，采用RRM(Rodrigues’ rotation matrix)对式(3)作空间旋转.其步骤为：

(1) 求旋转角度.选择未发生故障的轨迹曲线上的3点，它们分别记为

P

(

x

,

y

,

z

),

P

(

x

,

y

,

z

),

P

(

x

,

y

,

z

)，基于这3点构建电压暂降轨迹平面.令=-,=-.由于故障前后轨迹平面旋转的信息与法向量的相同，因此可通过法向量信息计算旋转信息.旋转前的、旋转后的、旋转轴(

l

,

m

,

n

)及旋转角

θ

分别为=×，

(4)

=(0,0,1)，

(5)

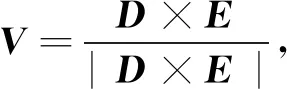
(6)

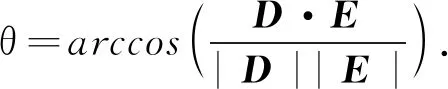
(7)

(2) 求RRM.通过旋转轴及旋转角，得到旋转矩阵为

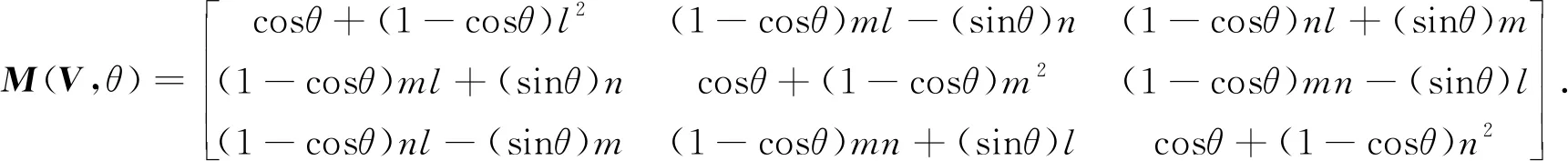
(8)

为了便于表达，将该矩阵简记为.(3) 使用旋转第

j

相轨迹.通过式(8)对第

j

相轨迹进行旋转，得到变换后的坐标向量为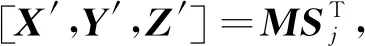

(9)

其中：′,′,′为变换后的列向量.利用式(9)将轨迹主体旋转至

xoy

平面，此时得到的图形为双椭圆.变换矩阵的表达式为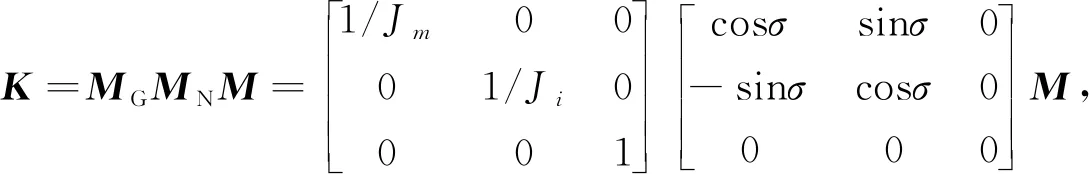

(10)

其中：为椭圆标准化矩阵；为椭圆化圆矩阵；

J

,

J

,

σ

分别为椭圆长半轴、短半轴及倾角.在采样频率及工频一定的情况下，矩阵不变.用代替式(9)中的，对要判断类型的三相信号依次变换，可获得需要的点坐标.通过检测可得到三相信号在某时刻的3点，将这3点分别与圆心相连得到三相相量图，再旋转该三相相量使其特征相落于横轴.式(9)经变换，再经相关运算可得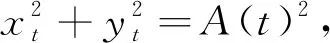

(11)

其中：(

x

,

y

)为最终坐标.(11)式表明相空间坐标经过上述处理后，可使三相轨迹主体最终化为同心圆.此同心圆由无扰动信号变换得到的参考圆及电压暂降信号变换得到的非参考圆组成.由式(11)可知参考圆的半径为1.已知参考圆的情况下，可得非参考圆的半径，进而求出暂降深度.通过同心圆可使各相信号离散后的相位均匀.从三相轨迹的周期性可知，相间相位差等于相间圆弧对应的圆心角.

1.3 基于相空间重构的电压暂降故障分类

对于故障持续时间大于1周期的情况，电压暂降故障分类步骤为：

(1) 检测得到发生电压暂降的一相，对该相作变换并得到暂降起止的两条过渡线.从起始过渡线与轨迹主体中获得相关信息.

(2) 寻找该相扰动的初始稳定点.寻找该点的方法为：若某点的前5点位于参考圆或过渡线上，其后5点位于非参考圆上，则该点为该相扰动的初始稳定点.然后，通过检测得到与该点时刻相同的其他两相扰动的初始稳定点.

(3) 检测另外两相是否发生电压暂降.对电压暂降发生相，判断对应点是否位于非参考圆上；对电压暂降未发生相，判断对应点是否位于参考圆上.若判断结果均为是，则进入步骤(4)；若不全为是，则将步骤(2)所得的点位置向后推一位，重复步骤(2)，(3).

(4) 分别将步骤(3)得到的3点与圆心相连，得三相相量图.

(5) 通过三相相量图得到相间相位差、幅值，将其与

ABC

分类图进行对比，得到扰动类型.对于故障时间不足1周期的情况，以其中任一暂降相为例进行说明.该相连续5点的原始数据经相空间延迟，可得到3个相空间点，利用矩阵对该3点进行变换，若变换后的3点均位于同一圆上，则将此圆作为该相暂降的轨迹.其他两相同理.然后，参考持续时间在1周期以上的情况，处理三相轨迹，得到电压暂降故障分类.

2 仿真实验

该文设置的采样频率为12 800 Hz.构造的归一化三相电压信号为

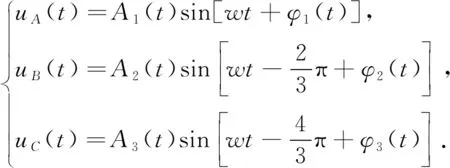
(12)

通过式(12)中未发生暂降的某相3个不共线的相空间点，得到矩阵为

(13)

为了验证该文方法的可行性，建立9类电压暂降故障仿真模型，然后将9类仿真模型的三相信号重构到相空间.通过矩阵获得的坐标，可得图1.图1中，红色、绿色、蓝色实线分别表示

A

,

B

,

C

三相的相空间曲线；蓝色有向实线代表相量，位于水平位置的为

A

相量，以

A

相量为基准顺时针先后出现的为

B

，

C

相量.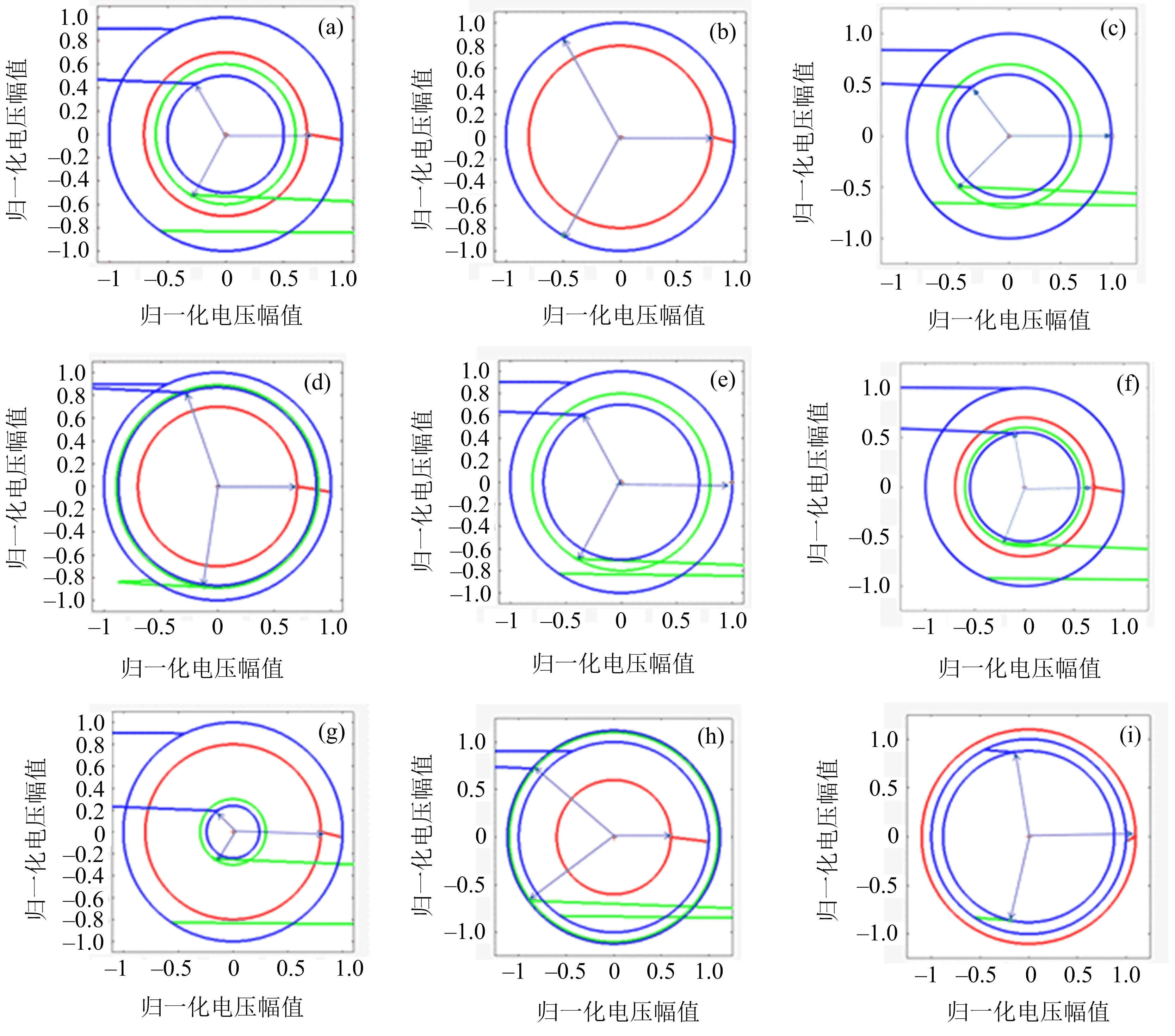

图1 9类电压暂降故障仿真模型的相量图

通过获得的三相相量图，结合预设数据，可得表1，2.

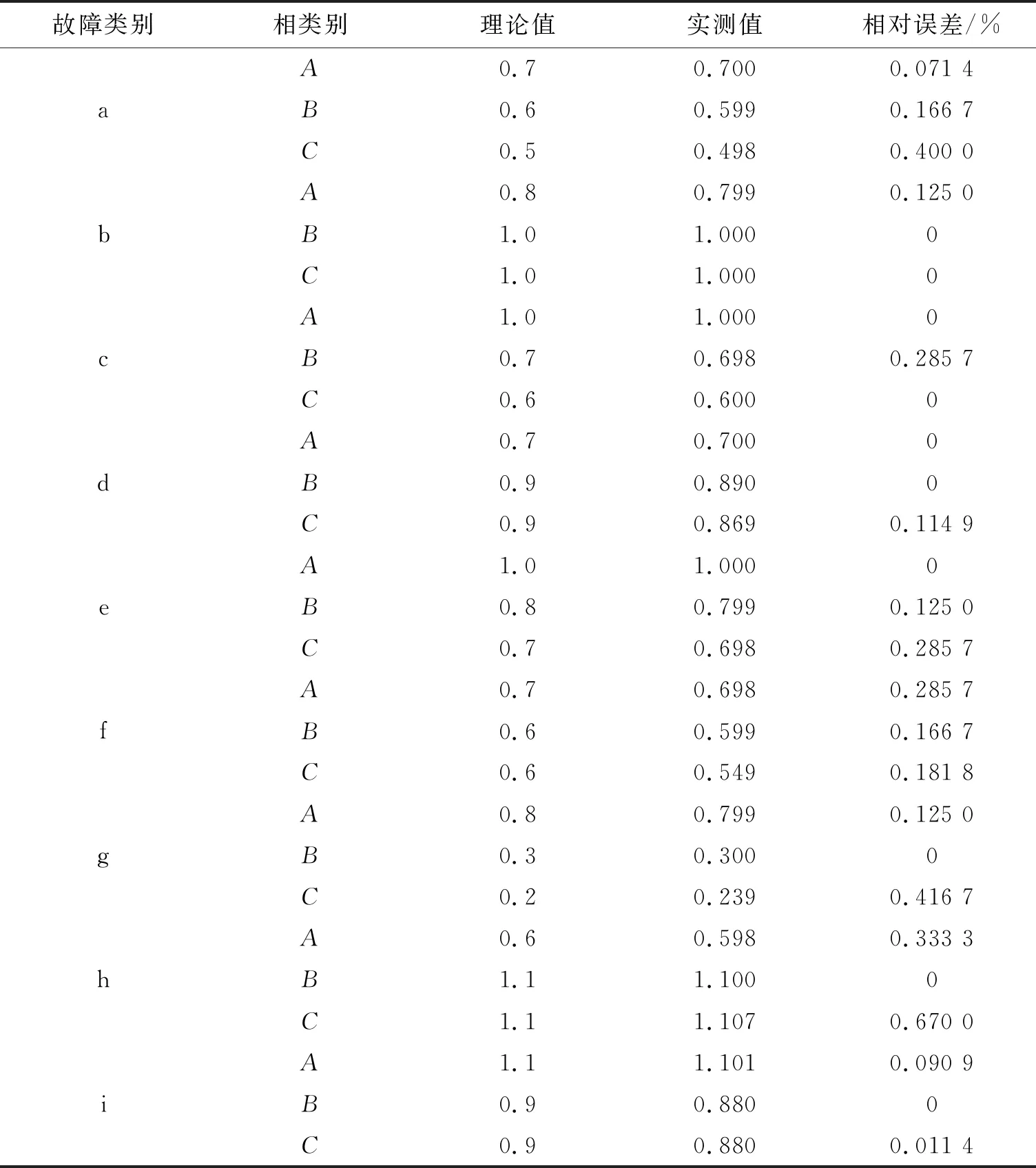
表1 9类电压暂降故障仿真模型的归一化电压幅值

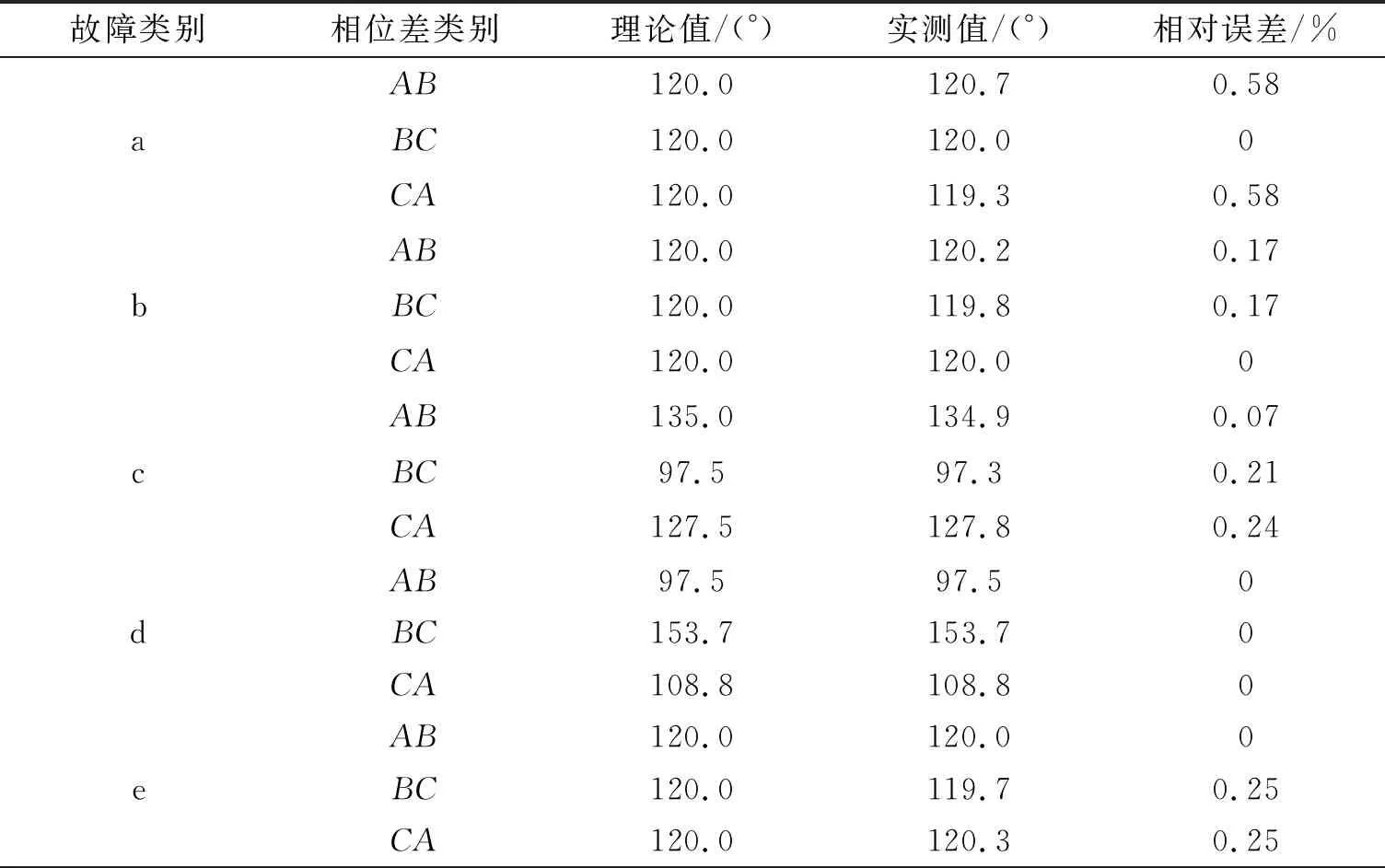
表2 9类电压暂降故障仿真模型的相位差

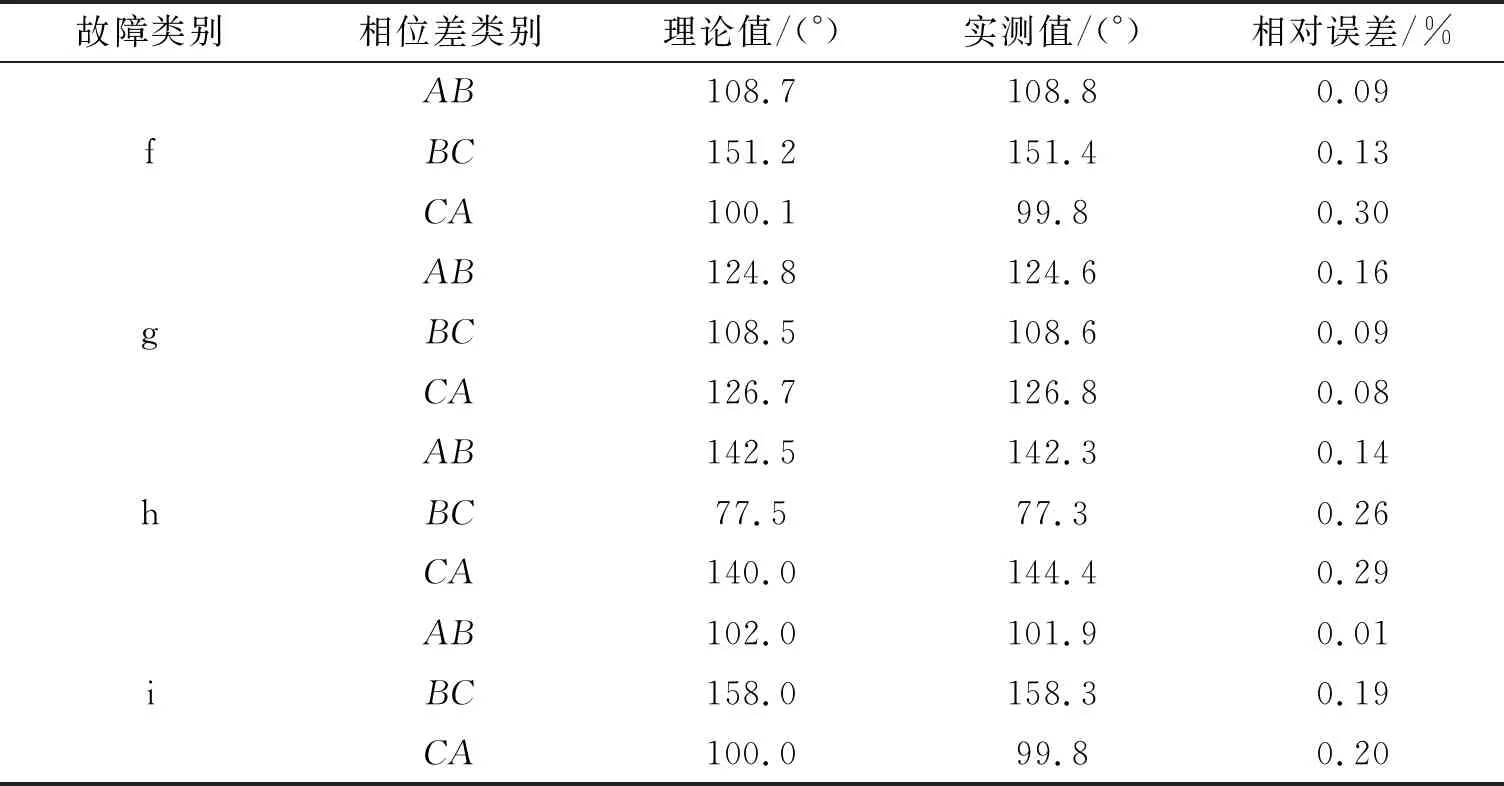
续表2

以图1(c)为例，根据表1,2可知：三相

A

，

B

，

C

的幅值依次为1，0.698，0.6；

AB

，

BC

，

CA

相位差依次为134.9，97.3，127.8°.可见，其故障类型为c类，与设置的类型一致.根据同样的分析可知，图1中的其他8类的二者类型也一致.由表1可知，各相幅值的实测值与理论值的最大相对误差为0.67%，最小相对误差为0.由表格2可知，相位差的最大相对误差为0.58%，最小相对误差为0.

3 算例分析

某制造型工业园区由于重型电力负载较多，电压暂降故障时有发生，经常受到用户投诉，故选取该园区变电站作算例.

3.1 算例1

根据该园区变电站某次电压暂降故障的三相数据，绘制出三相波形图.三相电压波形及相量图如图2所示，图2(a)中虚线框为一个周期的数据.

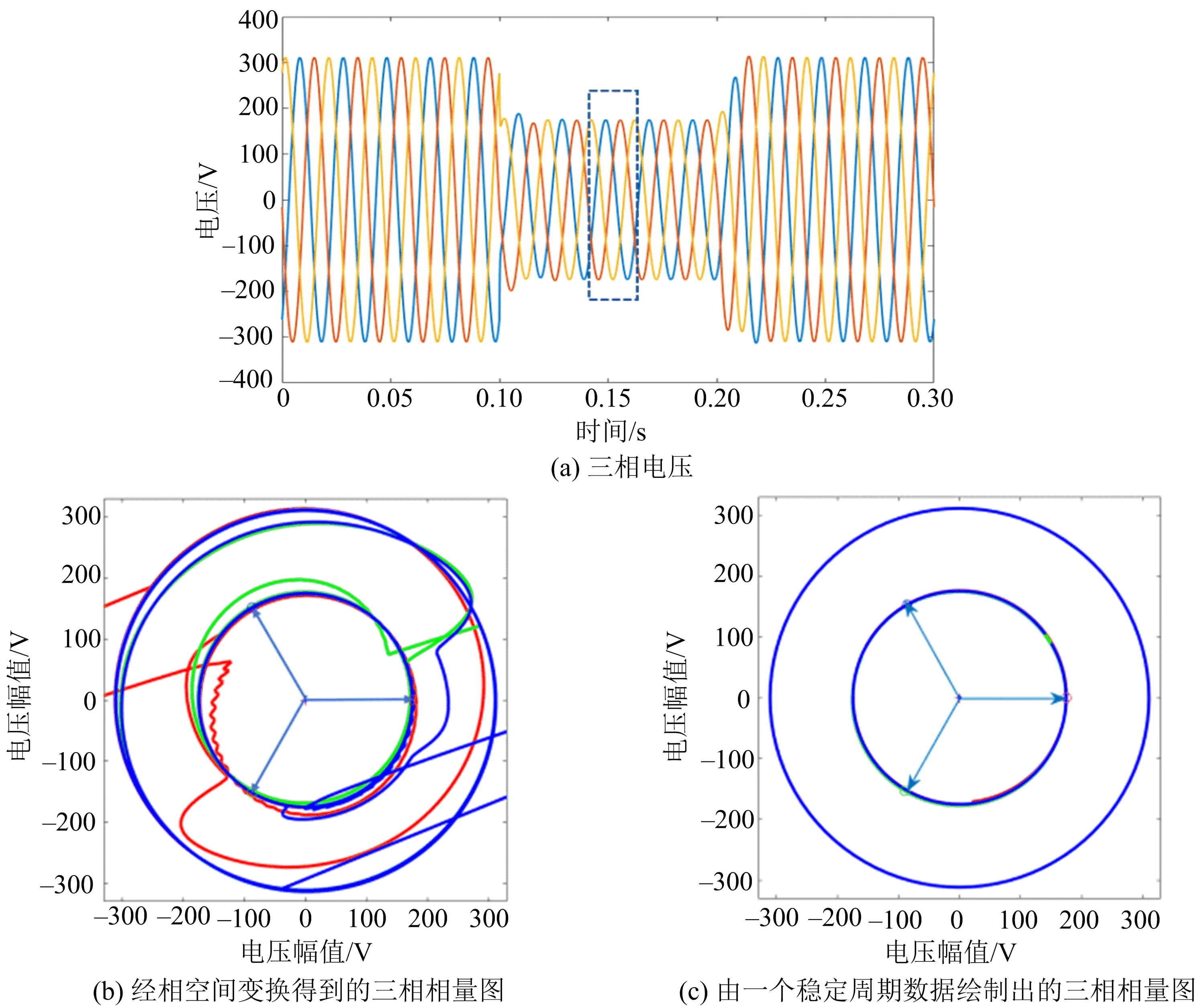
图2 三相电压波形及相量图

由图2(a)可知：幅值为311 V的

A

，

B

，

C

三相电压信号在0.1 s附近发生电压暂降，经过短时间的电压波动后分别稳定为振幅为174.97，174.99，174.99 V的正弦波，即电压暂降深度为0.437 4，0.437 3，0.437 3；0.2 s时，三相电压信号迅速恢复为原信号.由图2(b)，(c)可得表3所示的数据.

表3 暂降深度及相位差

由图2及表3可知，该次电压暂降类型为a类，与实际情况相符，表明该文方法在判断持续时间为1周期以上的暂降类型时是有效的.

3.2 算例2

从该园区变电站数据库中，选取另一项电压暂降故障原始数据，其波形如图3所示.

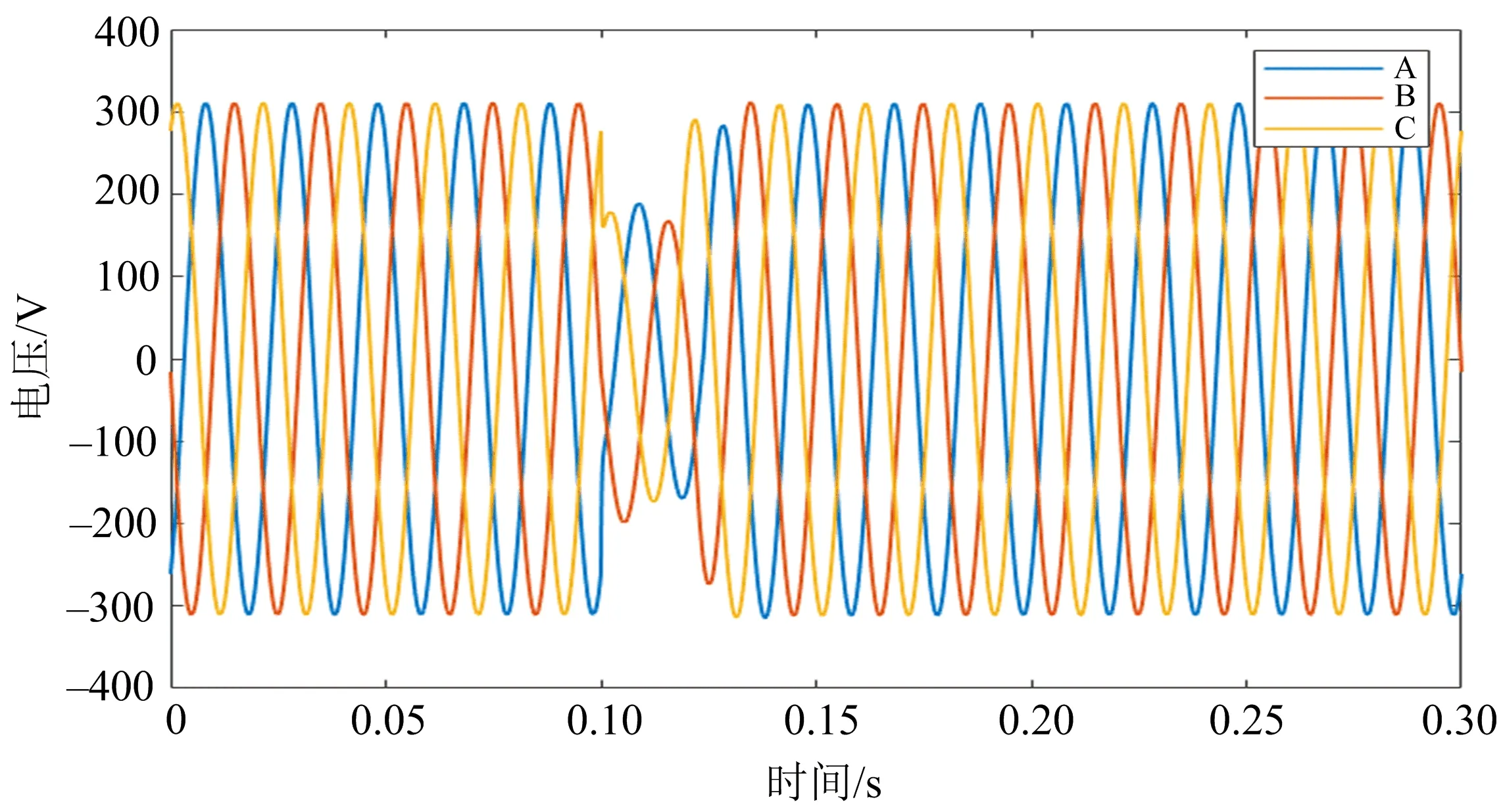
图3 电压波形

由图3可知，算例2故障持续时间不足1周期，原因为故障的及时消除.将图3所示波形图转化为三相相量图，如图4所示.

图4 三相相量图

由图4得到的相位差及暂降深度如表4所示.

表4 由图4得到的相位差及暂降深度

由图4及表4可知，该暂降类型为a类，与实际暂降类型相同，表明该文方法在判断持续时间不足1周期的暂降类型时具有可行性.

4 结束语

笔者使用相空间重构，对原始信号进行椭圆标准化、椭圆化圆操作获得同心圆.利用暂降到达稳定状态时的3点，得到三相相量图.对所得的相量图进行分析，得到电压暂降的分类结果.仿真实验及算例分析结果表明：基于相空间重构的电压暂降分类方法具有可行性.因此，该方法具有一定的工程应用价值.