极大类的capable 3-群
2021-01-14 04:27李志秀
安徽大学学报(自然科学版) 2021年1期
李志秀
(晋中学院 数学系,山西 晋中 030600)
对于一个给定的群G
, 若存在另一个群H
,使得H
/Z
(H
)≅G
,则称G
可以充当中心商, 或称G
为capable群. 早在1938年Baer在文献[1]中开始研究中心商问题,后来许多学者都研究过此问题.对中心商问题的研究,P.Hall在他的p
-群研究的奠基性论文中做了如下评论:“一个群G
需要满足什么条件才可以充当另一个群H
的中心商群,这是个有趣的问题,得到大量的必要条件是比较容易的,但要得到充分条件却很难.”此外,中心商问题也与覆盖群的Schur’s理论及射影表示有联系.文献[9-10]借助群的扩张理论,通过换位子计算分别得到了交换的capable群和亚循环的capable群.文献[11]得到了内交换的capable群.论文得到了一些极大类的capable3-群,并且由群G
构造出了群H
,使得H
/Z
(H
)≅G
.若无特别说明,文中所用的符号和概念均取自文献[12-13].
1 主要结果
下面给出论文的主要结果. 文中讨论的均为极大类的3阶群.
定理1
若G
为群G
=〈a
,b
,c
,d
,e
|e
=d
=1,a
=e
,b
=d
e
,c
=e
,[b
,a
]=c
,[c
,a
]=d
,[d
,a
]=e
〉,其中
[c
,b
]=[c
,d
]=[d
,b
]=[d
,e
]=1,或者
G
=〈a
,b
,c
,d
,e
|a
=e
=d
=1,b
=d
e
,c
=e
,[b
,a
]=c
,[c
,a
]=d
,[d
,a
]=e
〉,其中
[c
,b
]=[c
,d
]=[d
,b
]=[d
,e
]=[e
,a
]=1,则G
是capable 群.证明
G
同构于第一个群时,从3阶交换群出发,作循环扩张可构造出H
,使得H
/Z
(H
)≅G
.设交换群A
=〈d
〉×〈e
〉×〈f
〉≅Z
×Z
×Z
3,令映射σ
:d
→df
,f
→f
,e
→ef
, 再把它扩充到整个A
上, 可证σ
是A
的3阶自同构.设〈b
〉是3阶循环群,b
=d
e
且b
在A
上的作用与σ
相同. 令B
=A
〈b
〉=〈b
,d
,e
,f
〉, 则|B
|>=3.在B
中规定映射β
:b
→bf
,d
→df
,e
→e
,f
→f
,再把它扩充到整个B
上, 可证β
是B
的3阶自同构.设〈c
〉是3阶循环群,c
=e
, 且c
在B
上的作用与β
相同,令C
=B
〈c
〉, 则|C
|>=3.在C
中规定映射γ
:b
→bc
,c
→cd
,d
→de
,e
→e
, 再把它扩充到整个C
上, 可证γ
是C
的3阶自同构.设〈a
〉是3阶循环群,a
=e
, 且a
在C
上的作用与γ
相同,令H
=C
〈a
〉, 则|H
|>=3.H
=〈a
,b
,c
,d
,e
,f
|f
3=e
=d
=1,a
=e
,b
=d
e
,c
=e
,[b
,a
]=c
,[c
,a
]=d
,[c
,b
]=f
,[d
,a
]=e
,[b
,d
]=[d
,c
]=[b
,e
]=f
〉,其中:[e
,a
]=[e
,c
]=[e
,d
]=[f
,a
]=[f
,b
]=[f
,c
]=[f
,d
]=[f
,e
]=1,中心〈f
〉是3阶循环群,H
/Z
(H
)≅G
,G
是capable 群.注
G
同构于第二个群时, 在C
中令c
=e
f
,a
=1, 便可得到相应的H
,使得H
/Z
(H
)≅G
.定理2
若G
为群G
=〈a
,b
,c
,d
,e
|a
=e
=d
=1,b
=d
,c
=e
,[b
,a
]=c
,[c
,a
]=d
,[d
,a
]=e
〉,其中:[c
,b
]=[c
,d
]=[d
,b
]=[d
,e
]=[e
,a
]=[e
,b
]=1,则G
不是capable 群.
H
=〈a
,b
,Z
(H
)〉, 因为[b
,c
]在中心里,所以有[b
,c
]=[b
,c
]=[bc
,bd
]=[b
,c
][b
,d
][c
,d
],
b
,d
]=1,[b
,c
]=[b
,c
]=[d
,c
]=[c
,d
]=1,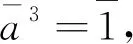
b
,a
]=[b
,a
][c
,a
][d
,a
]=[b
,a
][c
,a
][b
,a
]=[c
,a
]=[c
,a
],c
与a
交换,c
属于中心, 矛盾,G
不是capable 群.定理3
若G
为群G
=〈a
,b
,c
,d
,e
|a
=e
,e
=d
=1,b
=d
,c
=e
,[b
,a
]=c
,[c
,a
]=d
,[c
,b
]=[d
,a
]=e
〉,其中
[c
,d
]=[d
,b
]=[d
,e
]=[e
,b
]=1,或者
G
=〈a
,b
,c
,d
,e
|a
=e
,e
=d
=1,b
=d
,c
=e
,[b
,a
]=c
,[c
,a
]=d
,[c
,b
]=[d
,a
]=e
〉,其中
[c
,d
]=[d
,b
]=[d
,e
]=[e
,b
]=1,则G
不是capable 群.

c
,a
]=[e
,a
]=1,c
与a
交换,又[c
,b
]=[c
,b
][e
,a
]=[c
,b
]=[c
,b
]=[cd
,bc
]=[c
,b
][e
,d
][d
,c
][d
,b
],
c
,a
]=[c
,a
]=[c
,a
]=[c
,a
][d
,e
],[d
,e
]=1,故[d
,c
]=1,即1=[d
,c
]=[b
,c
]=[b
,c
]=[b
,c
],c
与b
交换,c
属于中心, 矛盾,G
不是capable 群.定理4
若G
为群G
=〈a
,b
,c
,d
,e
|a
=e
=d
=1,b
=d
,c
=e
,[b
,a
]=c
,[c
,a
]=d
,[c
,b
]=[d
,a
]=e
〉,其中
[c
,d
]=[d
,b
]=[e
,a
]=[d
,e
]=[e
,b
]=1,则G
不是capable 群.
H
=〈a
,b
,Z
(H
)〉, 由于[c
,b
][e
,a
]=[c
,b
]=[c
,b
]=[cd
,bc
],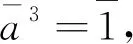
b
,a
]=[b
,a
][c
,a
][d
,a
]=[b
,a
][c
,a
][b
,a
]=[c
,a
]=[c
,a
],故
1=[c
,a
]=[e
,a
]=[d
,c
]=[b
,c
],c
与a
,b
交换,c
属于中心, 矛盾,故G
不是capable 群.
