混合型交换四元数矩阵的指数形式
2021-01-14 04:26孔祥强
安徽大学学报(自然科学版) 2021年1期
孔祥强
(菏泽学院 数学与统计学院,山东 菏泽 274015)
四元数的概念由爱尔兰数学家Hamilton提出,其形式为H
={a
+a
i+a
j+a
k;a
,a
,a
,a
∈R},i=-1,j=-1,k=-1,ijk=-1.James Cockle给出了分裂四元数的概念,其形式为H
={a
+a
i+a
j+a
k
;a
,a
,a
,a
∈R},i=-1,j=1,k=1,ijk=1. 与四元数代数H
不同,分裂四元数代数H
不是除环,且含有零因子、幂零元和幂等元.在分裂四元数的研究方面已取得系列成果.Segre在文献[7]中首次研究了交换四元数代数问题,即乘法满足交换律的四元数问题,开辟了四元数研究的新领域.对交换四元数代数的研究已取得了部分成果.文献[11]对交换四元数进行了详细阐述,文献[12]对交换四元数进行了分类,文献[13]重点研究了椭圆型交换四元数及其矩阵.论文研究的是混合型交换四元数,从两个方面展开:①给出混合型交换四元数的复表示及性质;②得到混合型交换四元数矩阵的指数形式及相关定理,并通过算例验证了求指数形式新方法的有效性.1 交换四元数的复表示及性质
设H
={a
=a
+ia
+ja
+ka
;a
,a
,a
,a
∈R},R为实数域,且i=-1,j=1,k=-1,ijk=1,ij=ji=-k,jk=kj=-i,ki=ik=j,称满足条件的交换四元数a
为混合型交换四元数.为叙述方便,以下将混合型交换四元数简述为交换四元数.符号Re(a
),Im(a
)分别表示混合型交换四元数a
的实部和虚部,即Re(a
)=a
,Im(a
)=ia
+ja
+ka
.设a
,b
∈H
,则a
+b
=(a
+b
)+i(a
+b
)+j(a
+b
)+k(a
+b
),ab
=(a
b
-a
b
+a
b
-a
b
)+i(a
b
+a
b
-a
b
-a
b
)+j(a
b
+a
b
+a
b
+a
b
)+k(a
b
-a
b
-a
b
+a
b
).定理1
任一交换四元数均可表示为复数域C
上的2阶矩阵.证明
设a
=a
+ia
+ja
+ka
∈H
,a
,a
,a
,a
∈R,则a
=(a
+ia
)+j(a
-ia
)=c
+j·c
,其中c
=a
+ia
,c
=a
-ia
,c
,c
∈C
.定义映射φ
:H
→H
,对于任意的b
∈H
,有φ
(b
)=ab
,则φ
为双射且φ
(1)=a
1=c
+jc
,φ
(j)=a
j=c
+jc
.依此映射,可定义交换四元数集合为2阶复矩阵集合
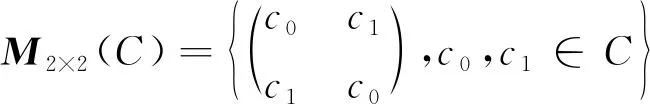
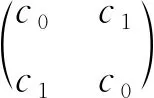


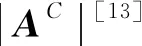
定理2
设,∈×(H
),则:
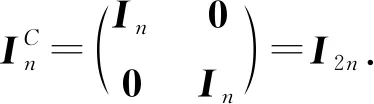
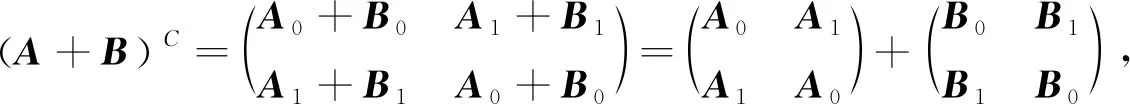
(3) 由
=(+)+j(+),则

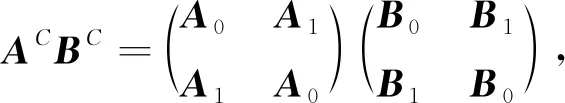
2 交换四元数矩阵的指数表示
对任意的n
阶实矩阵或复矩阵,其指数形式记为g
,g
∈×(R
).g
的幂级数表示为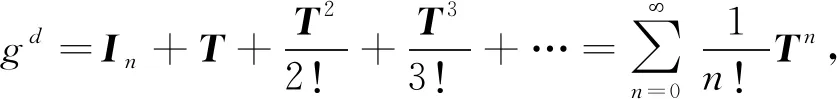
(*)
该级数总是收敛的. 该级数既定义了指数映射,也定义了矩阵间的映射,对任意的n
阶交换四元数矩阵,(*)式成立,且收敛.定理3
设∈×(H
),为的复表示形式,则g
=(g
).证明
由定理2,有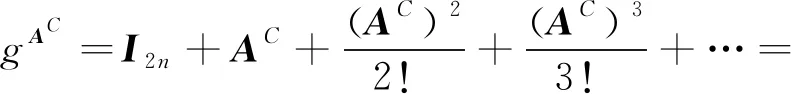
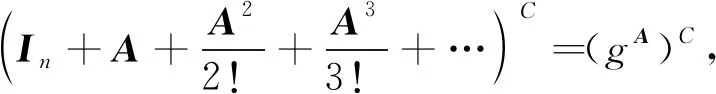
g
=(g
).定理4
设,∈×(H
),且满足=,则g
+=g
g
.证明
设,的复表示形式分别为,,由定理2,有()=,()=,又=,故=.由于结论对复矩阵也是成立的,所以
g
(+)=g
+=g
g
=(g
)(g
),即 (g
+)=(g
g
),所以g
+=g
g
.下面给出求交换四元数的指数形式的方法.
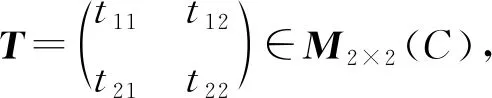
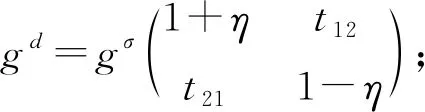

a
的复表示,则由定理3,可得a
的指数形式g
.
定理5
设,∈×(H
),且可逆,则g
=g
.证明
由定理2,有()=()=(),由于对复矩阵结论成立,则g
()=g
(),故
g
()=g
(),又由定理3,有
g
()=(g
),所以
g
()=(g
),g
=g
.设=(a
)∈×(H
),称的主对角线元素的和为的迹,记作tr,即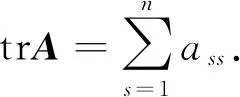
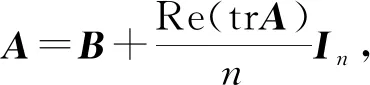
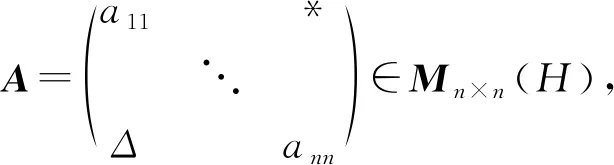

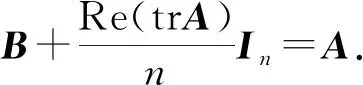
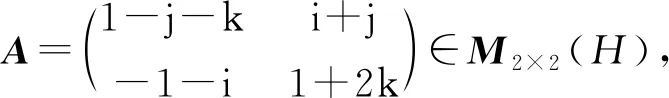
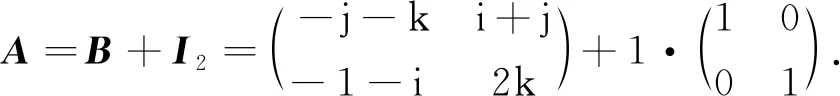
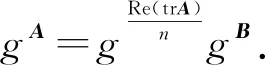
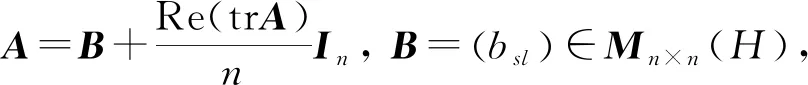
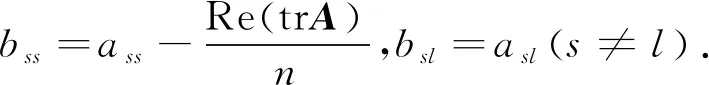
由于

由定理4,有
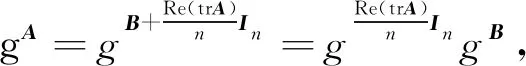
由定理2,有

则
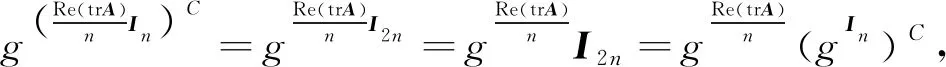
故
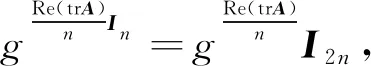
所以
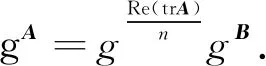
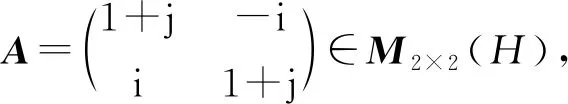
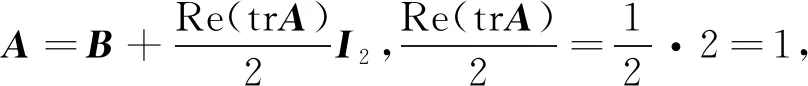
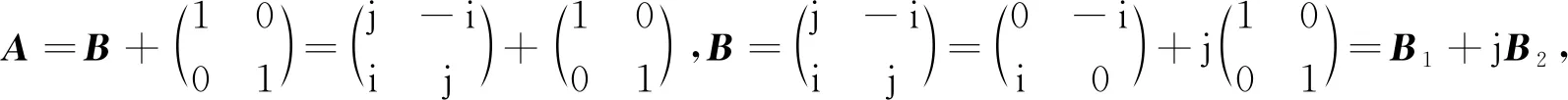
则

其特征值为2,-2,0,0.
令
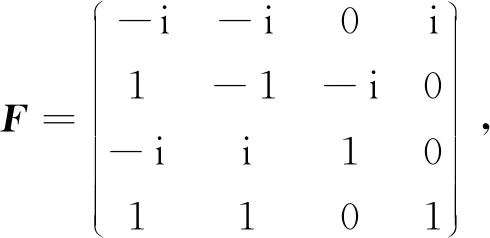

由复矩阵指数表示的性质,有
g
=diag(e,e,1,1)=
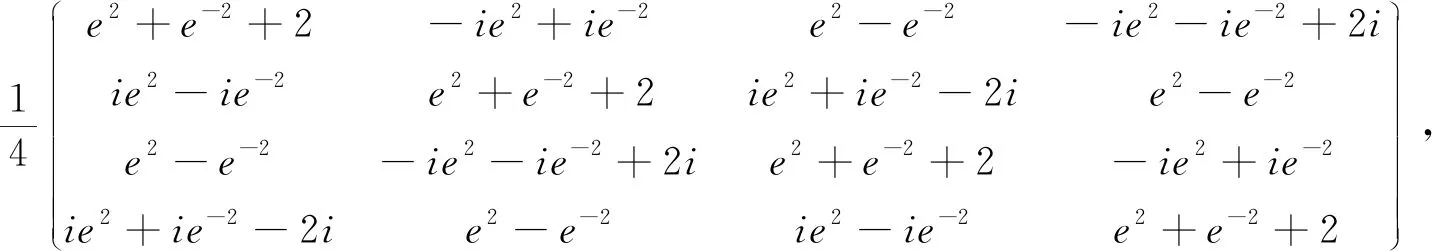
由定理3,有
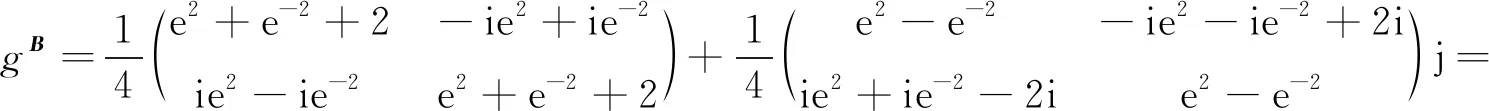
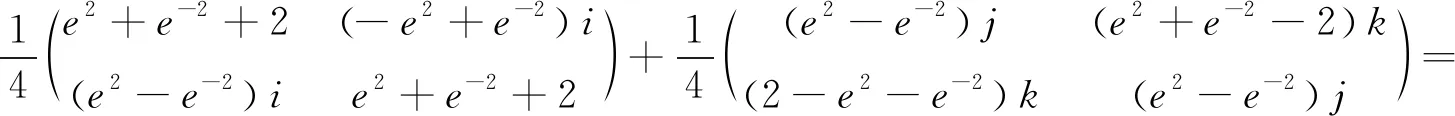
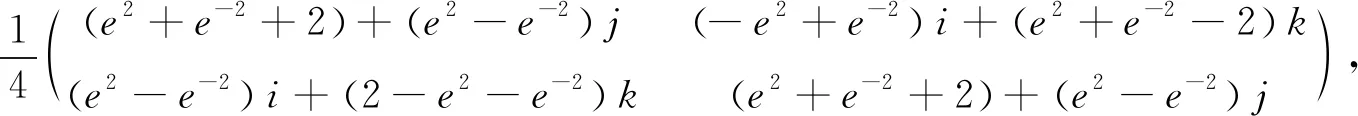
由定理6,有

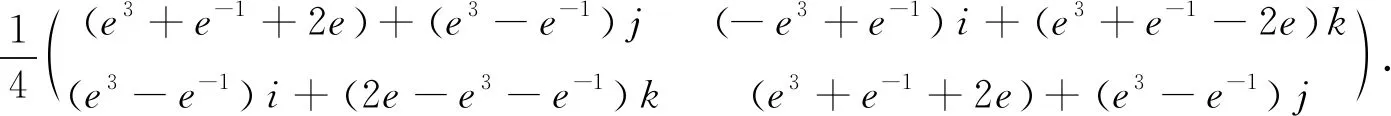
定理7
设∈×(H
),tr为的迹,则|g
|>=g
2Re(tr).证明
令=+j,,∈×(C
),为的复表示,则=,=diag(λ
,λ
,…,λ
2),λ
(p
=1,2,…,2n
)为的特征值,所以g
=g,两边取行列式|g
|>=||>|g
|>||>,又|g
|>=g
g
…g
2,故|g
|>=g
++…+2=g
tr,即
|g
|>=|(g
)|>=|g
|>=|g
|>=g
tr.由复表示定义及迹的性质 tr=tr(+)=2Re(tr),故|g
|>=g
2Re(tr).推论1
设∈×(H
),则|g
|>=1⟺Re(tr)=0.定理8
设∈×(H
),λ
为的实特征值,则g
为g
的特征值.证明
由题意,存在非零的交换四元数向量x
,满足x
=λx
,则x
=λ
x
(l
=1,2,…).又
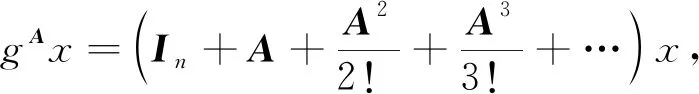
即
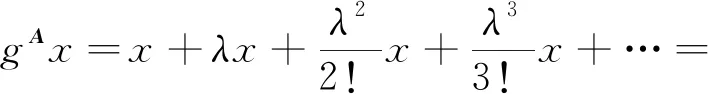
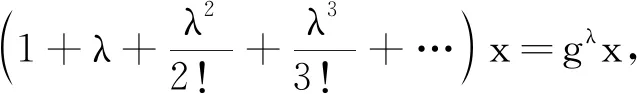
g
为g
的特征值,且属于特征值g
的特征向量仍为向量x
.推论2
设∈×(H
),λ
为的实特征值,则g
也为g
的特征值.3 结束语
交换四元数理论在控制论、群论、计算机图形图像学等方面均有重要的应用.交换四元数的类型主要分为椭圆型、双曲型、抛物型和混合型等. 通过对混合型交换四元数的研究,给出了利用混合型交换四元数的复表示求混合型交换四元数矩阵指数形式的新方法. 以复表示为基础,也可展开对混合型交换四元数矩阵的逆矩阵问题、可对角化问题、广义对角化问题的研究.

