血细胞生成模型的数值振动性分析
2021-01-14 04:26刘子婷
安徽大学学报(自然科学版) 2021年1期
王 琦,刘子婷
(广东工业大学 应用数学学院, 广东 广州 510006)
考虑如下非线性延迟微分方程
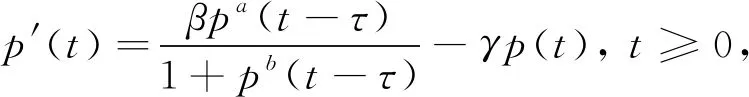
(1)
其中
β
,γ
,τ
∈(0,∞),a
,b
∈N.(2)
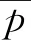
a
=0时, El-Sheikh等得到了方程(1)的振动性和全局吸引性条件. Saker对于广义的a
和b
进行了拓展并改进了文献[3]中的相应结果. 当a
=1时, Hale等给出了方程(1)的数值模拟和混沌问题的结论. 有关方程(1)的更多信息, 可参阅文献[6]及其参考文献. 然而,以前的结果都是关于理论分析方面的,很少考虑数值行为. 作者的目的是研究方程(1)的数值振动性和非振动性. 作为微分方程研究领域中最受关注的问题之一, 振动性越来越受到人们的青睐.定理1
考虑差分方程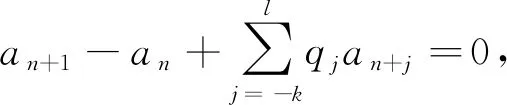
(3)
假设k
,l
∈N,q
∈R,j
=-k
,…,l
,则下面两个陈述是等价的:(i) 方程(3)的每一个解都是振动的;
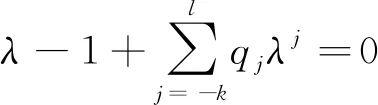
定理2
对于差分方程a
+1-a
+pa
-+qa
=0,(4)
其中:k
,p
,q
>0, 方程(4)的所有解振动的充分必要条件是q
∈(0,1)且
引理1
对于m
≥M
,有(i) (1+d
/(m
-θd
))≥e.当且仅当d
>0时,1/2≤θ
≤1;d
<0时,φ
(-1)≤θ
≤1.(ii) (1+d
/(m
-θd
))d
<0时,0≤θ
<1/2;d
>0时,0≤θ
≤φ
(1).其中:φ
(x
)=1/x
-1/(e-1),M
是正的常数.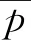

(5)
令
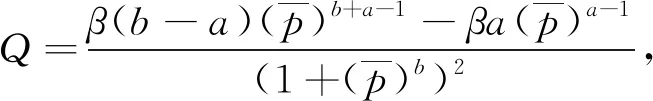
(6)
则(5)式可化为
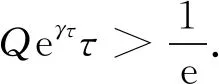
(7)
1 离散格式
为了减少计算量和复杂度,首先引入方程(1)的一个不变振动变换, 然后将数值方法应用到方程被简化后的形式.
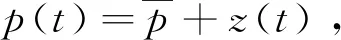
z
′(t
)+γf
(z
(t
))+Qf
(z
(t
-τ
))=0,(8)
其中
f
(u
)=u
,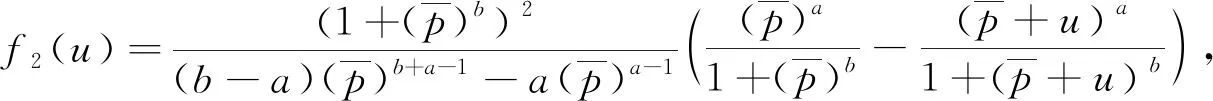
并且满足
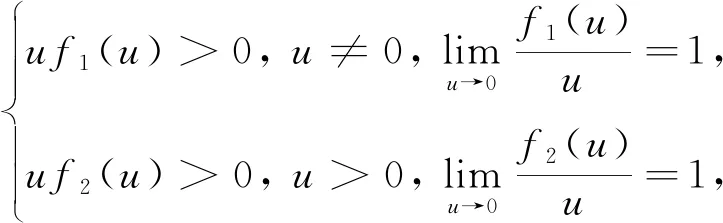
(9)
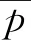
h
=τ
/m
为步长,m
为正整数, 将θ
-方法 (0≤θ
≤1)应用于(8)式,得z
+1=z
-hθγf
(z
+1)-hθQf
(z
+1-)-h
(1-θ
)γf
(z
)-h
(1-θ
)Qf
(z
-),(10)
其中:z
+1和z
+1-分别是(8)式中z
(t
)和z
(t
-τ
)在t
+1处的近似.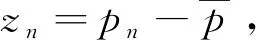
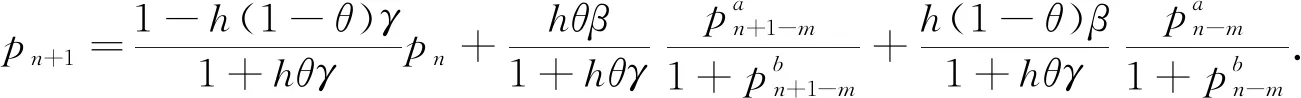
(11)
2 数值解的振动性
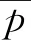
将(10)式线性化为
z
+1=z
-hθγz
+1-hθQz
+1--h
(1-θ
)γz
-h
(1-θ
)Qz
-,(12)
整理得
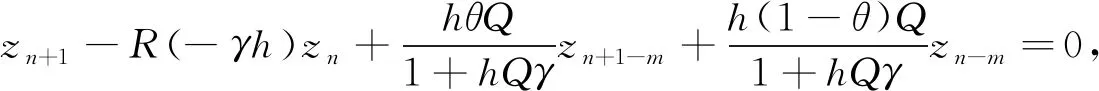
(13)
其中:R
(x
)=(1+(1-θ
)x
)/(1-θx
)是θ
-方法的稳定函数. 由文献[12]知, 如果(13)式在满足条件(9)时振动, 则(10)式就是振动的.接下来, 将考虑θ
-方法是否保持了方程(1)的振动性,即在定理3成立的前提下, 研究(11)式在什么条件下是振动的.引理2
方程(12)的特征方程由下式给出λ
=R
(-h
(γ
+Qλ
-)).(14)
证明
由方程(12)和R
(x
)的表达式可证.引理3
如果定理3成立, 则特征方程(14)在0≤θ
≤0.5时没有正根.证明
设A
(λ
)=λ
-R
(-h
(γ
+Qλ
-)). 由引理1得R
(-h
(γ
+Qλ
-))≤exp(-h
(γ
+Qλ
-)).(15)
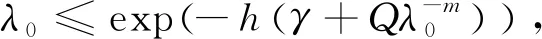
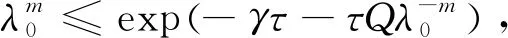
(16)
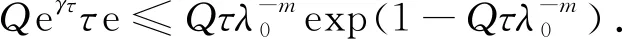
分以下两种情形讨论:
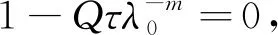

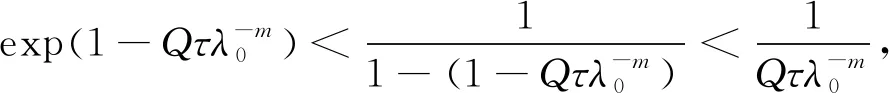
即
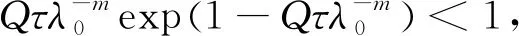
Qτ
ee<1,仍与(7)式矛盾,因此对于λ
>0,有A
(λ
)=λ
-R
(-h
(γ
+Qλ
-))≥λ
-exp(-h
(γ
+Qλ
-))=B
(λ
)>0,这就意味着特征方程(14)没有正根. 证毕.
不失一般性, 假设当0.5<θ
≤1时,总有m
>1.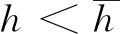
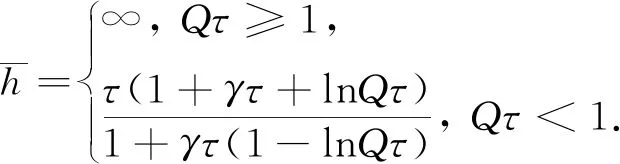
(17)
证明
易知函数R
(-h
(γ
+Qλ
-))当λ
>0时关于参数θ
单调上升, 有
接下来证明下式在一定条件下成立
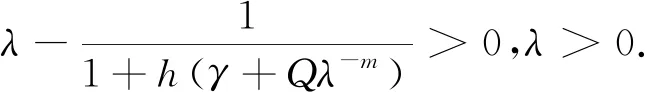
(18)
记
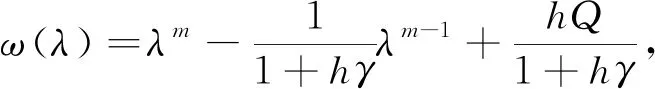
(18)式的左侧可化为
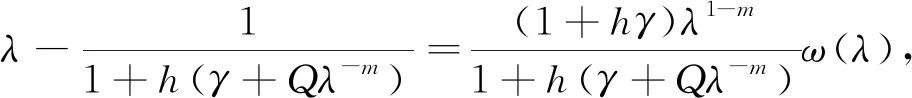
λ
>0时,ω
(λ
)>0. 显然,ω
(λ
)是如下差分方程的特征多项式
ω
(λ
)没有正根当且仅当下式成立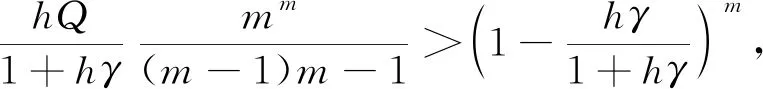
此式可化为
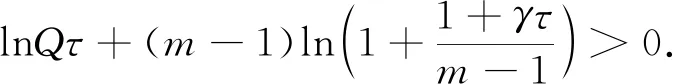
(19)
因此, 考虑以下两种情形:
情形1:若Qτ
≥1, 由m
>1知(19)式成立.情形2:若Qτ
<1,h
<τ
(1+γτ
+lnQτ
)/(1+γτ
(1-lnQτ
)), 有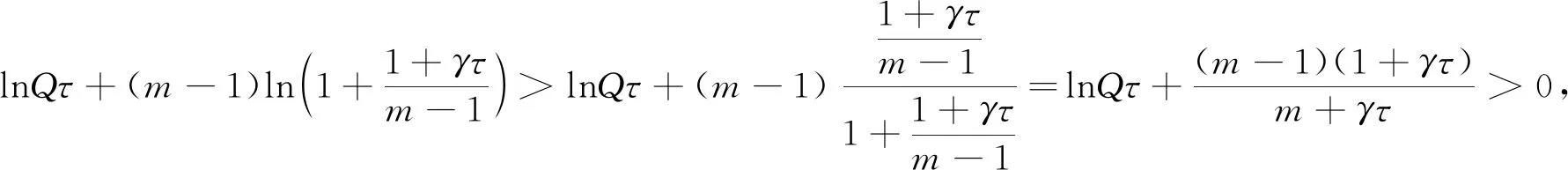

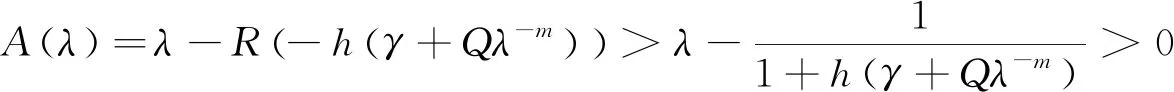

应用(9)式、引理3,4和定理1,得到论文的第一个主要结论,即定理4.
定理4
如果定理3成立, 则(11)式在如下条件下是振动的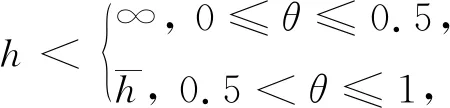
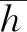
3 非振动数值解的渐近行为
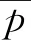
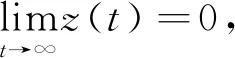
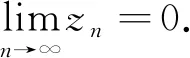
证明
不妨假设对于充分大的n
,z
>0,有f
(z
)>0,f
(z
)>0. 由(10)式,得z
+1-z
+hθQf
(z
+1-)+h
(1-θ
)Qf
(z
-)=-hθγf
(z
+1)-h
(1-θ
)γf
(z
)<0,(20)
故z
+1-z
<0, 从而{z
}单调下降,则存在η
≥0,使得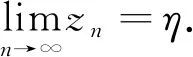
(21)
下面证明η
=0. 如果η
>0, 则存在N
∈N和ε
>0,使得n
-m
>N
,0<η
-ε
<z
<η
+ε
,从而z
->η
-ε
,z
-+1>η
-ε
. 因此由(20)式,得z
+1-z
+hθQf
(η
-ε
)+h
(1-θ
)Qf
(η
-ε
)<0,这就隐含着z
+1-z
<C
<0, 其中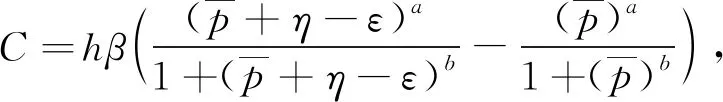
z
→-∞ (n
→∞), 与(21)式矛盾. 证毕.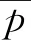
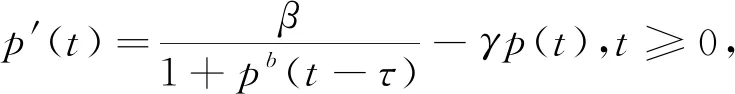

(22)
在ρ
=1时的情形. 文献[15]讨论了方程(22)数值解的振动性,得到的结论是论文相应结果的特殊情形.4 数值算例
先考虑如下问题
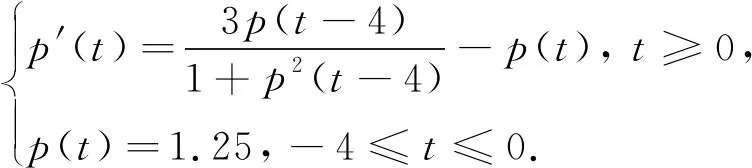
(23)


图1 问题(23)的解析解(a)和数值解(b)
再考虑如下问题
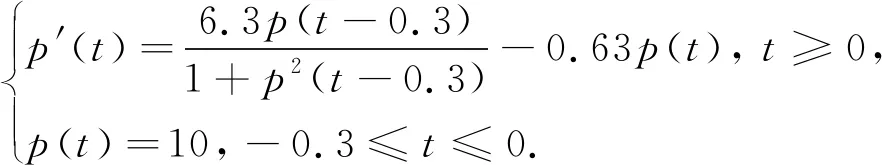
(24)
易验证条件(5)不成立, 所以问题(24)的解析解非振动. 图2(a)、(b)分别为问题(24)的解析解与数值解.在图2中令m
=30,θ
=0.4, 则
n
→∞),即数值方法保持了问题(24)的非振动解的渐近性, 这与定理5一致.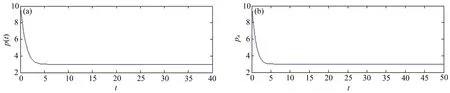
图2 问题(24)的解析解(a)和数值解(b)
总之, 从图1,2中可以看出,θ
-方法分别保持了问题(23)的振动性和(24)的非振动性.
