合理利用几何画板 提升学生数学核心素养

姚晋秋

摘  要 在高三数学复习课中合理运用几何画板，可以帮助学生直观感受数学知识的内在联系，便于探究“定点定值”“轨迹方程”等动态问题，提高课堂效率，提升学生数学学科核心素养。

关键词 几何画板;高三数学;直线与圆;定点定值;轨迹方程;数学核心素养

中图分类号：G633.6    文献标识码：B

文章编号：1671-489X（2021）20-0066-03

1  教学背景分析

本节内容是高三数学一轮复习“直线和圆”的探究课，是对本章知识的总结和提升，尤其是对直线与圆位置关系中的动态问题进行复习。在这之前，学生已经系统复习了“直线方程”“圆方程”“直线与圆的位置关系”及“圆与圆的位置关系”等知识，并能熟练掌握基本题型的解题方法，但涉及动态问题难免会束手无策。因此，无论是从高考应试方面，还是从提升学生数学学科核心素养方面，本节内容都是不可缺少的。此外，高三数学一轮复习的下一章内容是“圆锥曲线”，“定点定值”“最值问题”“轨迹方程”向来是“圆锥曲线”中的重点与难点，而本节探究内容所用的思想方法对下一章的复习具有类比和启发作用，因此，这就使得本节知识变得尤为重要。

几何画板是高中数学常用的教学软件，不仅能画出几何图形，还具备变换、度量、动画、跟踪轨迹等诸多功能。用几何画板辅助数学课堂教学已经变成常态，尤其是数学新授课，它不仅融合了PPT中的功能，而且使得原本抽象的静态图变得生动而形象，让学生对问题的分析更加直观，激发学生学习数学的兴趣。在高三复习课中合理地运用几何画板，能给学生创造一个实际“操作”几何图形的环境，增强其对几何图形的感性认识，帮助其形成丰富的几何背景经验，从而有助于对动态问题的理解和证明。

2  制定课前任务

探究直线与圆的动态问题是本节课的重点与难点，但如何才能自然地引出动态问题呢？笔者制定如下课前任务。

1）直线l：y=kx-3与圆C：x2+y2=16的位置关系是

2）若直线l：y=kx-3与圆C：x2+y2=4有两个不同交点A、B，且AB=2，则k=

3）过点作圆x2+y2=4的切线方程为

4）过直线l：x-y+4=0上一定点P（2，6）作圆O：x2+

y2=4的切线，求：①切线方程;②切线长;③切点所在的直线方程。

【设计意图】

1）会用几何法和代数法判断直线与圆的位置关系，而题1中所给的含参直线恒过一个定点且此定点在圆的内部，这既是判断直线与圆位置关系的第三种方法，又为下文探究1作热身。

2）复习直线与圆相交及相切基本问题，指出圆心到直线的距离d是解题关键，圆本身的几何性质决定所有的动态问题都离不开这个基本量。

3）第四题中所给的点P是定點且位置比较特殊，学生会用多种方法求解。利用几何画板变动P的位置之后，如图1所示，让学生明白，多种解法中的“两圆公共弦所在直线即为切点所在的直线”为最优解法，且自然地引出探究1。

3  课堂探究提升

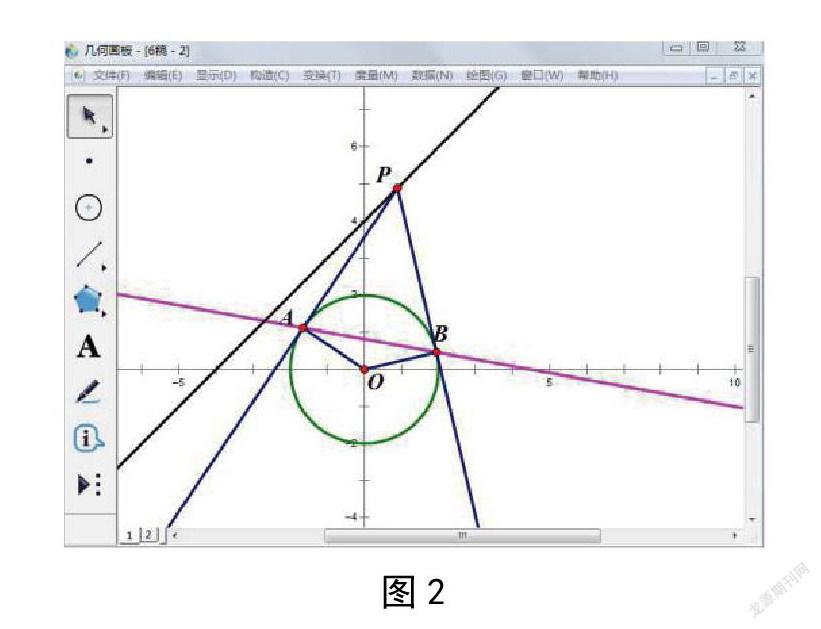
【探究1】如图2所示，过直线l：x-y+4=0上任意一点P（x，y）作圆O：x2+y2=4的两条切线，切点分别为A、B，探究直线AB是否过定点。

【设计意图】拖动点P，追踪直线AB，轨迹如图3所示，定点一目了然。启发学生思考：如何在有了“形”的直观后，用“数”的运算得到定点坐标？在这一过程中提升学生数学运算、直观想象等核心素养。

【解题方法】设P（m，m+4），通过课前任务可以知道，A、B两点所在直线方程为mx+（m+4）y=4，所以恒过定点Q（-1，1）。

【探究2】过直线l：x-y+4=0上任意一点P（x，y）作圆

O：x2+y2=4的两条切线，切点分别为A、B，探求A、B中点的轨迹方程。

【设计意图】取AB的中点M，追踪点M的轨迹，拖动点P，得到点M的轨迹。消参法和定义法是求轨迹方程的两种常用方法，引导学生用这两种方法探求轨迹方程，在解题过程中培养学生逻辑推理、数学运算等核心素养。

【解题方法1】如图4所示，点M即为AB与OP的交点。由探究1知直线AB的方程为mx+（m+4）y=4，直线OP的方程为（m+4）x-my=0，两式联立消去m，得M的轨迹方程为x2+x+y2-y=0（y≠x）。

【解题方法2】由探究1知直线AB恒过定点Q（-1，1），又因为QM⊥MO，所以M点在“以OQ为直径的圆”上。考虑到点M与点O不会重合，所以轨迹是一个不封闭的圆，如图5所示，轨迹方程为（x+1/2）2+（y-1/2）2=1/2（y≠x）。

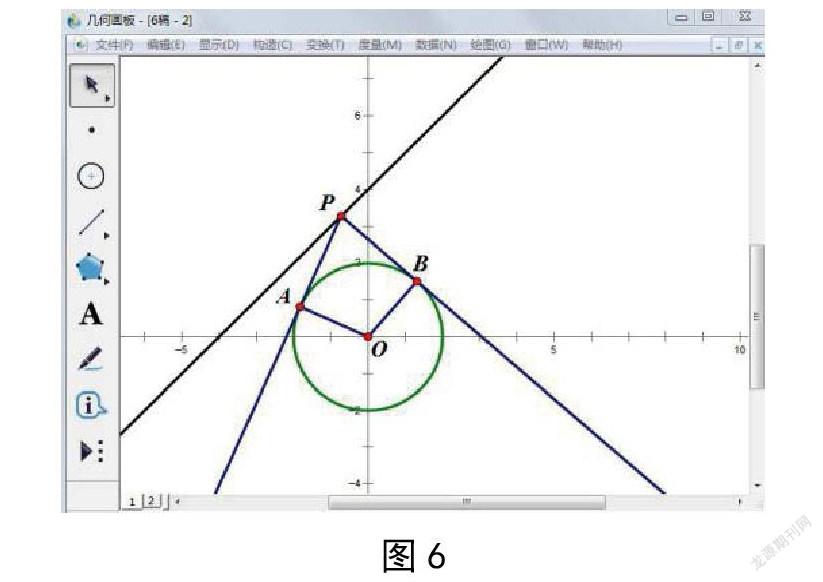
【探究3】如图6所示，过直线l：x-y+4=0上任意一点P（x，y）作圆O：x2+y2=4的两条切线，切点分别为A、B，探究四边形PAOB面积是否存在最小值。

【设计意图】最值问题是解析几何中常见的题型，怎样把四边形的面积表示成某个变量的函数形式呢？如图7所示，拖动点P，四边形面积随之改变。学生的第一反应是四边形面积随着切线PA的变化而变化，但考虑到点P和点A都是动点，PA的范围不容易求，由于有了课前任务作为铺垫，此时学生自然会想到连接PO，用PO的长度作为变量来表示四边形面积。这个过程有效发展了学生的数学建模核心素养。

【解题方法】S四边形PACB=2S△PA0=A0·PA=A0·

，PO最小值为O到直线x-y+4=0的距离，所以四边形PAOB面积的最小值为4。

【探究4】已知P为直线l：x-y+4=0上的点，若圆O：x2+y2=4上存在点A、B，使得∠APB=60°，求点P横坐标的取值范围。

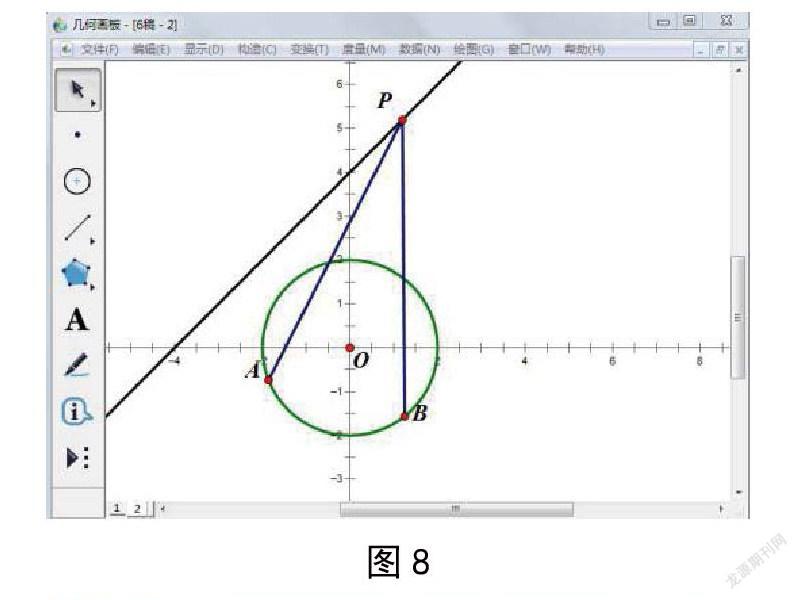
【设计意图】“存在性问题”是近年来考试的热点。前三道探究问题中，PA、PB均是切线，在探究4中A、B变成动点，思维难度又上一个台阶。首先固定点P，任意拖动点A、B，让学生直观感受∠APB的大小变化，如图8所示。此时会发现，当PA、PB分别为圆的切线时，∠APB最大。其次拖动点P，发现当点P离圆O越远，∠APB越小，也就不可能存在点A、B，使得∠APB=60°;而点P越靠近圓O，∠APB越大，会存在无数组点A、B，使得∠APB=60°。最后，学生自然会去寻求∠APB的“临界状态”，如图9所示，找到解题突破口。

【解题方法1】设P（m，m+4），连接PO，如图10所示，在△PAO中，sin∠APO=AO/PO。由分析知∠APO≥

30°，所以PO=AO/sin∠APO≤4，进而求出点P横坐标的取值范围是[-4，0]。

【解题方法2】在掌握方法1的基础上，引导学生理解：在平面内，若PO≤4，则P点的轨迹是“以O为圆心，4为半径的圆及其内部”;又P在直线x-y+4=0上，所以点P为直线与圆面的公共部分，如图11所示，从而可以求出点P横坐标的取值范围。此种方法需要找出点P的“隐藏轨迹”，在解题中应用广泛。

4  课后复习巩固

为了巩固课堂所学知识，笔者制定课后作业：复习教科书中相关的作业与练习，整理直线与圆动态问题错题，提出一个有价值的问题并尝试解决它。

【设计意图】数学基础知识与数学基本技能是我国高中数学课程目标的重要构成部分。通过课堂学习，切实提高学生“从数学角度发现和提出问题的能力、分析和解决问题的能力”。数学课程不应仅仅满足于教给学生一些结论，而应该给学生以更多数学思想、精神的浸润。这节在几何画板辅助下的“直线与圆动态探究”复习课，将会在很长一段时间内让学生铭记在心。事实上，从学生的作业反馈来看，确实收到不错的教学效果，学生提出诸如“如图6，求线段AB的取值范围”等很有探究价值的问题。

5  总结

数学学科核心素养的培养不是无源之水、无本之木、必须接地气，要有良好的学习基础与具体教学过程目标来支撑。几何画板的合理利用，一改高三复习课高强度、沉闷的课堂氛围，能使原本枯燥、抽象的知识变得生动有趣，更能激发学生的科学探索精神，有助于他们复习迎考。如何用好几何画板，这对施教者提出新的挑战，广大教师要更加激流勇进，不断提高自身学科素养，真正做到“立德树人”。■

参考文献

[1]教育部基础教育课程教材专家工作委员会.普通高中数学课程标准（2017年版）解读[M].北京：高等教育出版社，2018：64-65.

[2]徐新兵.翻转课堂提升物理学科核心素养：以《反冲运动 火箭》为例[J].中国信息技术教育，2019（20）：64-66.

[3]徐新兵.基于DIS的翻转课堂教学实践研究提升物理学科核心素养：以《单摆》教学为例[J].中国现代教育装备，2018（20）：32-34.