尾流干涉下串联圆柱涡激振动数值模拟研究*

王晓凯 娄 敏

(中国石油大学(华东)石油工程学院)

0 引 言

T.KITAGAWA等[7]在亚临界雷诺数下改变间距比，研究了上游圆柱的尾流对下游圆柱流体力的影响。B.S.CARMO等[8]对两圆柱串联流动进行仿真分析，上游圆柱保持固定，下游圆柱仅允许在横流向自由振动，与孤立圆柱对比结果表明，串联圆柱的振动最大位移显著增大。郭晓玲等[9]对低雷诺数下(Re=150)等直径串联圆柱的流动干涉进行了数值模拟研究，发现圆柱间距比的改变会导致“锁定”区间发生变化。ZHAO M.等[10]重点关注了大圆柱对小圆柱尾流与振动的影响，在特定的间距范围内发现圆柱响应会出现4个不同的分区。宋振华等[11-12]研究了顺流向振动对横流向最大振幅和锁定区间的影响，同时针对3根附属杆抑制装置对立管所受流体力的抑制效果、泄涡模式及抑制机理进行了深入研究。F.J.HUERA-HUARTE等[13]改变上游圆柱与下游圆柱的直径比，通过振幅和流体力系数的变化讨论了尾流干涉的影响。娄敏等[14-15]在尾流干涉下考虑流固耦合作用对串联圆柱进行了仿真研究，发现随着约化速度增大，涡激振动远离“锁定”状态的多频现象逐渐减弱；同时采用不同的抑振装置对串联立管涡激振动抑制进行了试验分析，综合比较得出控制杆的抑制效果更佳。

从目前情况来看，对于圆柱涡激振动的研究已经趋于成熟，然而多数研究集中在单自由度情况下，同时涉及到小尺寸圆柱尾流干涉下的研究十分有限。为此，本文利用Fluent软件中的SSTk-ω湍流模型，基于新颖的Overset-Mesh方法对流场建模处理，通过雷诺平均法求解黏性N-S方程，并运用动网格技术实现流固耦合，针对小尺寸串联双圆柱在双自由度下的涡激振动位移响应、受力特性、运动轨迹以及涡脱模式进行二维仿真研究。研究结果可以为深海油气开发中立管的涡激振动分析提供理论依据。

1 数值方法

1.1 Overset Mesh

Overset Mesh又被称为重叠网格或者嵌套网格，重叠网格通常由一个背景网格和至少一个前景网格所组成，如图1所示。重叠网格是将流体计算域划分成多个简单的部件区域，然后各部件区域单独划分Parts网格，并将其嵌入到背景网格中，再通过Overset Interface连接重叠网格单元区域，在前景网格和背景网格的接连区域通过插值来实现流场信息的传递，迭代计算的过程中会不断搜索重叠区域边界，将真实的物理边界识别出来并参与计算。

图1 重叠网格构成图Fig.1 Composition of overset mesh

利用重叠网格技术可以处理具有小缝隙部件的相对网格运动，与传统网格相比，重叠网格对网格拓扑要求低，且网格生成相对容易，同时可以避免传统动网格技术所面临的网格动态更新时易出现的负体积现象，在网格运动期间始终能够保持很高的网格质量，实现了局部结构网格在非结构网格中的使用。Overset Mesh在计算流体力学工程实际应用中的流程如图2所示。

图2 重叠网格在数值计算中的流程Fig.2 Numerical calculation process of overset mesh

1.2 控制方程

不可压缩黏性牛顿流体的控制方程为N-S方程。在直角坐标系下，基于雷诺平均的连续性方程和动量方程分别为：

U=0

(1)

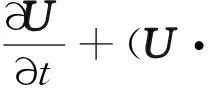
(2)

漩涡泄放对圆柱体作用力如图3所示。由图3可见，流体流经圆柱时会在其两侧产生漩涡泄放现象，在横流向方向产生升力FL造成横向运动，同时在顺流向方向产生脉动阻力FD造成顺流向的运动。升力与脉动阻力的表达式分别为：

(3)

(4)

图3 漩涡泄放对圆柱体作用力Fig.3 Acting force of vortex discharge on the cylinder

式中：CL为升力系数；CD为阻力系数，与雷诺数Re有关，无量纲；ρ为流体密度，kg/m3；D为圆柱体直径，m。

早期对于涡激振动的研究主要集中在较大质量比的圆柱，顺流向振幅极小，因此大多数研究选择忽略顺流向运动而采用主要观察横流向运动响应特征的单自由度模型。虽然顺流向的阻力FD通常要比横流向的升力FL小得多，但由于阻力周期是升力的2倍，所以顺流向阻力对圆柱结构的影响不可忽略。对于本文采用的小质量比圆柱，顺流向运动会对横流向造成影响，与横流向的单自由运动相比，两自由度运动能够使横流向获得相对较大的幅值。圆柱振动模型如图4所示。

图4 圆柱振动模型Fig.4 Cylindrical vibration model

本文根据圆柱在流场中的受力形式和运动情况将振动模型简化为双自由度(2-DOF)弹簧-质量-阻尼系统，便于研究顺流向与横流向之间的耦合运动。振动模型控制方程为：

(5)

(6)

式中：x、y分别为圆柱顺流向位移与横流向位移，m；m为圆柱质量，kg；c为结构阻尼系数；k为系统刚度系数；FD(t)为圆柱所受顺流向阻力，N；FL(t)为圆柱所受横流向升力，N。

2 数值模型

2.1 模型参数

数值模拟中圆柱模型的基本参数如表1所示。根据T.K.PRASANTH等[16]对网格尺寸的研究，当满足尾流区长度大于25D，整体高度区域大于20D时，圆柱体两自由度涡激振动的响应将不再受流体区域边界的影响。流场区域计算模型如图5所示。选取D=0.018 m，两圆柱为等径串联排布，圆柱间距比L/D=4(L表示两圆柱圆心间的距离)，整个流场区域设为40D×20D，下游圆柱尾流区域长度为26D。流场建模时基于Overset-Mesh技术进行网格划分，如图6所示。从图6可见，整个流场区域由矩形的蓝色背景网格和2个圆环形的红色前景网格组成，对圆柱体周围和漩涡发散区域进行加密处理，其他区域进行线性加密，逐渐增大网格密度，合理控制网格总量。通过设定初始流速的方式来控制流场雷诺数的变化，在设置计算区域的边界时，入口处采用速度边界(Velocity-inlet)，出口处采用压力边界(Pressure-outlet)，上、下两侧面为对称边界条件(Symmetry)，流场与立管重叠部分为无滑移壁面边界(Wall)。

表1 圆柱模型基本参数Table 1 Basic parameters of cylindrical model

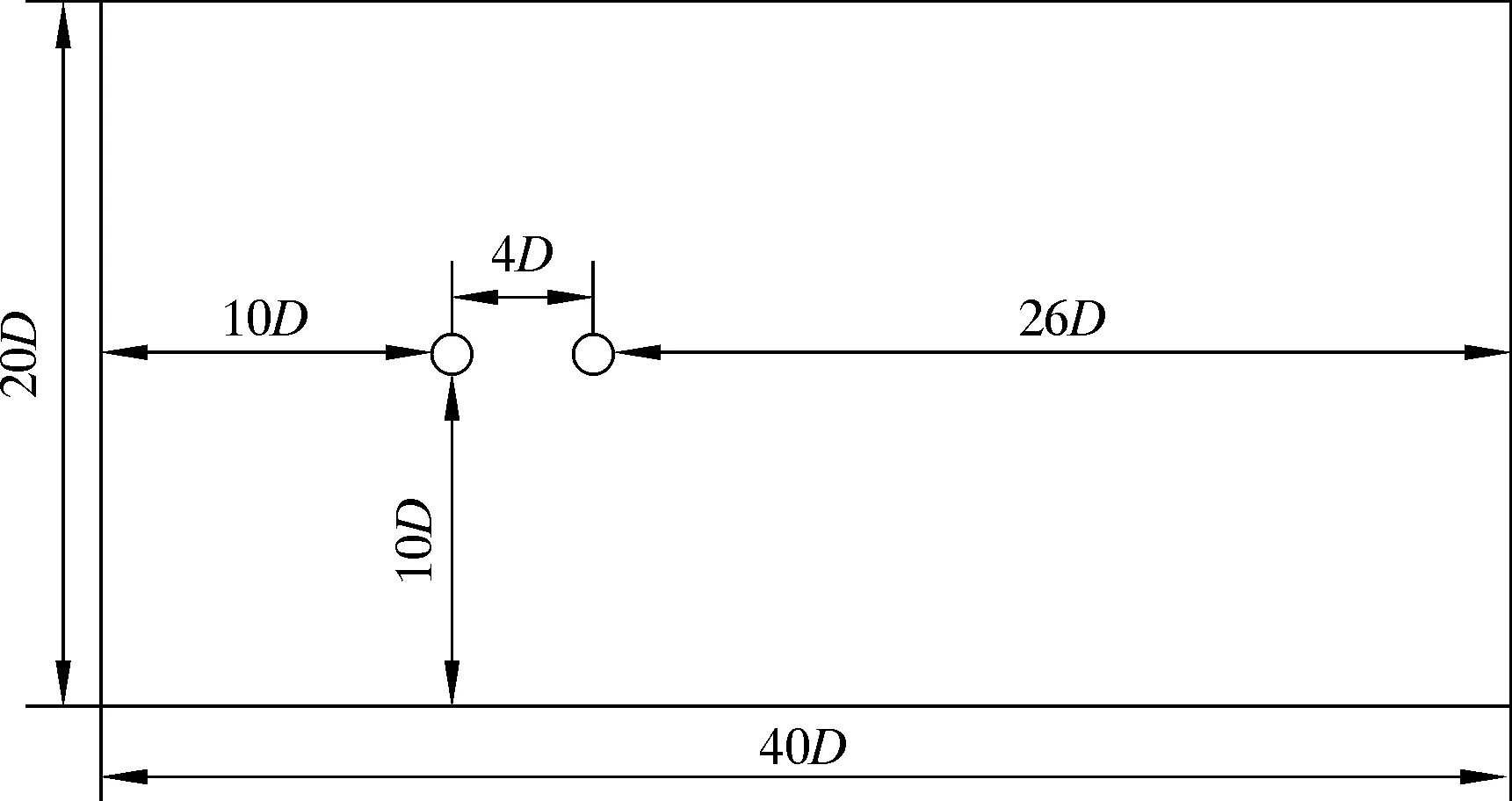
图5 流场区域计算模型Fig.5 Computational model of flow field area

图6 网格划分Fig.6 Mesh generation

本文数值模拟研究采用了SST(Shear Stress Transport)k-ω模型。SSTk-ω湍流模型属于雷诺平均法，是一种混合两方程的涡黏性分区模型，该湍流模型兼具了k-ω模型和k-ε模型的优点。当计算模型近壁面区域时，使用k-ω模型可以更好地解决边界层问题；而在远离壁面的区域则通过k-ε模型能够较好地模拟发展充分的湍流流动，这使得SSTk-ω模型的应用范围变得更加广泛。同时SSTk-ω模型考虑了湍流剪切应力的传播方式，并对ω方程的交叉扩散进行了合并，在求解负压梯度问题时会有更好的表现，整体计算的精确度和可靠性也得到提升。

2.2 模型验证

为检验上述计算模型与网格划分的可靠性，当雷诺数为200时，分别进行单圆柱绕流和间距比为4的串联双圆柱绕流数值模拟，得到相应的升力和阻力系数，模拟结果如图7所示。

图7 圆柱绕流模拟结果Fig.7 Simulation results of flow around the cylinder

将升力系数和阻力系数的相关数据通过MATLAB读取，并进行FFT(Fast Fourier Transform)傅里叶变换，得到漩涡脱落频率fs，再通过fs计算斯特劳哈尔数Sr：

(7)

将所得结果与文献[17-21]等数值模拟结果进行对比，如表2和表3所示。从表2和表3可见，模拟得到的升力系数CL、阻力系数CD和斯特劳哈尔数Sr与相关文献中的参考值均较为接近，确保了所选取的网格划分方法、数值求解格式等参数设置的可靠性，可采用该模型继续进行流固耦合的计算。表3中的CD1表示上游阻力系数，CD2表示下游阻力系数。

表2 单圆柱绕流结果对比Table 2 Comparison between simulation results of flow around a single cylinder

表3 双圆柱绕流结果对比Table 3 Comparison between simulation results of flow around two cylinders

3 计算结果

3.1 圆柱位移响应

对于圆柱结构的涡激振动问题，当圆柱的涡旋脱落频率fs与固有频率fn接近时，一般认为发生了“锁定”现象。图8给出了串联两圆柱的频率比fs/fn随约化速度Ur(表示来流速度和结构振动频率之间的无量纲参数)的变化关系。从图8可判断两圆柱的“锁定”区间为6≤Ur≤11。

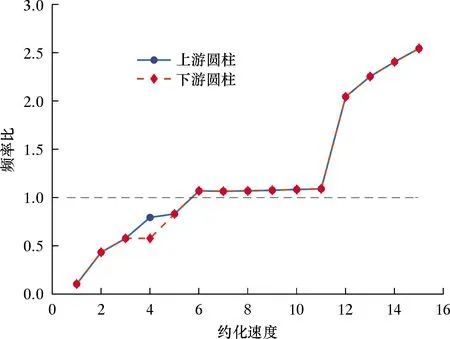
图8 频率比随Ur的变化关系Fig.8 Variation of frequency ratio with Ur

圆柱涡激振动响应随Ur的变化曲线如图9a所示。顺流向平均位移与圆柱直径之比X/D随约化速度的变化曲线如图9b所示。从图9a可见：采用振幅均方根与圆柱直径之比Y/D对横流向振动响应进行描述，两圆柱的横流向无量纲振幅Y/D随Ur发生振荡变化，观察发现横流向振幅可明显分为初始分支、上端分支和下端分支3个响应区间；当进入“锁定”区间内，下游圆柱的振幅迅速增大，当Ur=10时下游圆柱的Y/D取得最大值0.79，此时被“完全锁定”。因为频率比不再随约化速度的变化继续增大，漩涡之间相互融合使得漩涡强度得到提升，所以在流体与圆柱之间产生了剧烈的非线性动力相互作用，致使圆柱结构产生大幅度振动，形成上端分支的响应区间。从图9b可见：两圆柱的顺流向平均位移X/D呈现增大趋势；由于随着Ur的增大，流经圆柱结构的来流速度相应增加，圆柱在顺流向方向上受到的冲击作用越来越强，故顺流向平均位移持续增大。

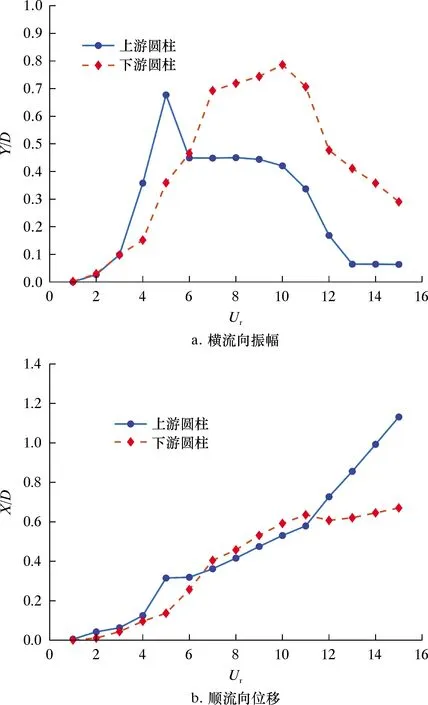
图9 圆柱涡激振动响应随Ur的变化曲线Fig.9 Variation of cylinder's vortex-induced vibration response with Ur

3.2 圆柱受力特性

图10为串联双圆柱在涡激振动过程中升力系数和阻力系数随Ur的变化关系。

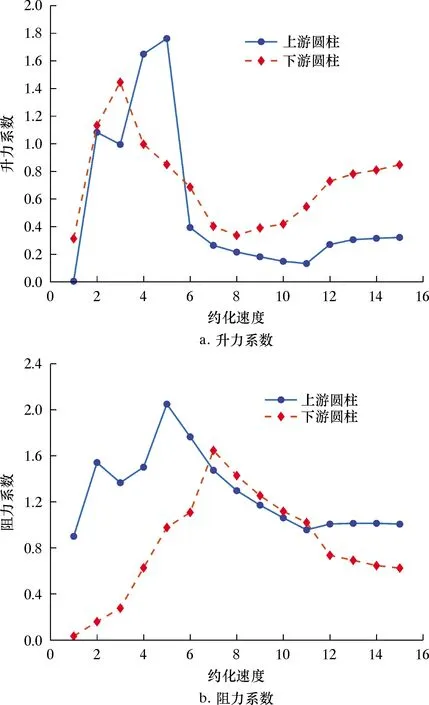
图10 升力系数和阻力系数随Ur的变化关系Fig.10 Variation of lift resistance coefficient with Ur

由图10a可见，两圆柱的脉动升力系数随Ur的变化过程总体相似，表现为先增后减再增的三段式进程，这说明约化速度Ur的改变对脉动升力系数有着显著的影响。由图10b可见，当Ur较小时，上游圆柱平均阻力系数始终大于下游圆柱，且下游圆柱的阻力峰值小于上游圆柱，而在Ur>6之后，两圆柱的平均阻力系数逐渐减小，下游圆柱阻力系数短暂大于上游圆柱。下游圆柱受到上游圆柱尾流干涉的影响，圆柱周围的实际来流速度小于上游圆柱，因此下游圆柱的平均阻力系数在低约化速度时均小于上游圆柱，同时峰值也会小于上游圆柱。在“锁定”区间内，下游圆柱横流向振幅迅速增大，明显大于上游圆柱，使得在来流方向上两圆柱已不在同一平面，上游圆柱无法继续对下游圆柱产生较大的影响，所以下游圆柱平均阻力系数在此期间短暂大于上游圆柱。随着Ur继续增大，最终两圆柱的平均阻力系数趋于稳定。

3.3 圆柱运动轨迹

图11为上游圆柱和下游圆柱的运动轨迹随Ur的变化关系。

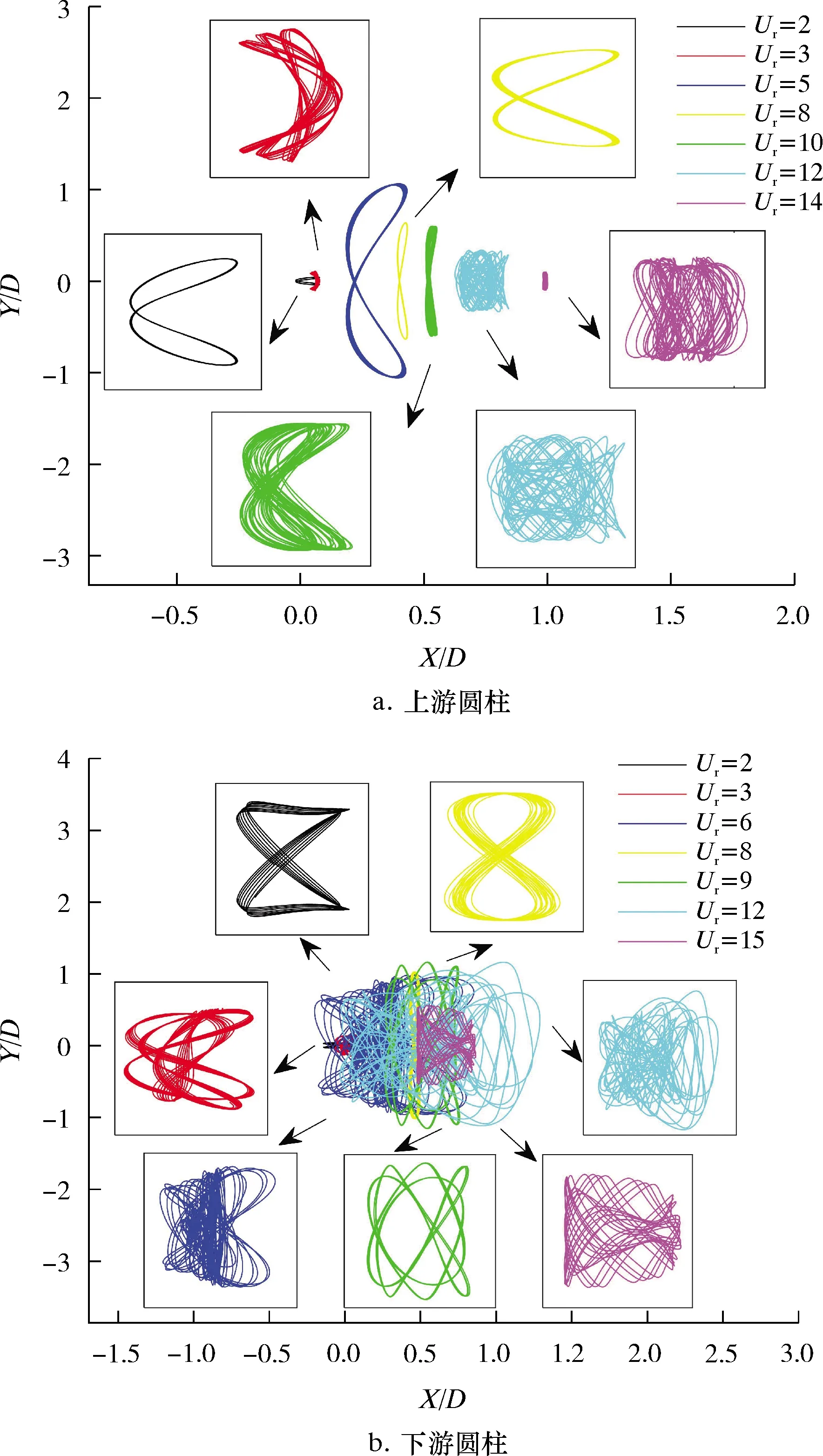
图11 圆柱运动轨迹随Ur的变化关系Fig.11 Variation of cylinder’s moving trajectories with Ur

从图11可发现：上游圆柱在初始分支和上端分支响应区间的运动轨迹以“8”字形、“新月”形封闭曲线为主，周期性并不稳定，这说明当间距比L/D=4时下游圆柱对上游圆柱振动模态的影响作用比较有限，仅引入些许的随机性扰动；当Ur继续增大，在离开“锁定”区间后，横流向振幅迅速减小，上游圆柱的运动轨迹逐渐向“椭圆”形转变；下游圆柱的轨迹形状随Ur的增大在“椭圆”形、“8”字形和“新月”形等之间转换，运动轨迹相比上游圆柱更加复杂。由于下游圆柱受到上游圆柱的遮蔽干扰以及尾流干涉作用的影响，故其呈现出不稳定的非周期性运动轨迹，此外，约化速度也对圆柱的运动有明显的影响。

3.4 圆柱尾涡脱落模式

图12为圆柱尾涡脱落模式随Ur的变化关系。

图12 尾涡脱落模式随Ur的变化关系Fig.12 Variation of wake shedding mode with Ur

从图12可以看出，当Ur<5时，上游圆柱无明显涡脱现象，因为此时来流速度较小，在圆柱两侧未能产生周期性漩涡脱落，所以串联圆柱的尾流在下游圆柱后方汇集形成一条涡带，使得圆柱系统尾流区内的漩涡以图12a的模式进行整体脱落。随着Ur不断增大，从图12c可见，Ur=8时尾涡脱落呈现“2S”模式，即每个周期内泄放两个漩涡。当进入“锁定”区间内，上游圆柱后方开始出现漩涡脱落，下游圆柱的漩涡脱落长度同时增加，上游圆柱分离的剪切层与下游圆柱侧面发生碰撞，两圆柱的漩涡在下游圆柱表面发生融合，使得漩涡强度提升，尾涡脱落模式因此发生变化。从图12d可见，Ur≥12时脱落模式由“2S”转变为“2P”。从上游圆柱一侧脱落的漩涡与下游圆柱表面发生碰撞，撞击后的漩涡一部分与下游圆柱同侧漩涡融合，另一部分跟随下游圆柱反向脱落的漩涡一起脱落，即每个周期内从下游圆柱两侧各释放一对逆向旋转的漩涡，最终导致尾涡脱落模式再次发生转变。

4 结 论

(1)Overset-Mesh技术操作方便，在网格运动期间能够保持很高的网格质量，可以较好地用于计算流体力学工程实际中。

(2)下游圆柱的“锁定”区间与上游圆柱保持一致，并未受到流动干涉的影响而产生后移现象，说明在间距比L/D=4条件下，上游圆柱对下游圆柱的尾流干涉作用相对较弱。

(3)在约化速度Ur=6附近存在一个临界值Ur-crit，当Ur>Ur-crit时，下游圆柱的横流向振幅大于上游圆柱，而当Ur

(4)在“锁定”区间内，上游圆柱脱落的漩涡与下游圆柱发生碰撞，同性质漩涡融合使得漩涡强度增大，尾涡脱落模式因此转变，下游圆柱振幅相应增大。串联圆柱的尾涡脱落模式随Ur增大会发生显著变化，进而深刻影响圆柱的运动响应和受力情况。