基于AMEsim液压增速回路仿真分析

邓均成，陶 柳，雷 雄，王 竞

（四川工程职业技术学院交通工程系，四川 德阳618000）

0 引言

增速回路用来使执行元件获得尽可能快的运动速度，缩短工作循环时间，以提高生产率和充分利用功率。该回路一般采用自重充油，增速液压缸等来达到增速的目的，所以又称为快速运动回路[1]。自重充油回路不需要增设辅助的动力源，结构简单，但是在活塞下行时液压缸上腔吸油不充分，容易导致增速不稳定，而增速液压缸能很好的克服这一缺点，在实际生活中应用广泛。

本文利用AMESim仿真软件建立了增速液压缸增速回路仿真模型[2]，对回路的增速特性进行了仿真分析，对相关参数进行了优化设计，为增速回路的精度提高提供了理论参考。

1 增速液压缸增速原理

采用如图1所示的利用增速液压缸（又称为快速活塞）的增速回路。活塞快速右行时，液压泵只给增速液压缸的小腔1供油，大腔2所需的液压油经液控单向阀3通过油箱4来补充，由于小腔1的有效工作面积小，所以此时活塞快速右行。当负载增加时，系统压力升高打开顺序阀5，压力油关闭液控单向阀3并进入大腔2，由于此时有效工作面积增大，活塞转入慢进。回程时，压力油打开液控单向阀3，大腔2的回油排回油箱4中，活塞实现快退。

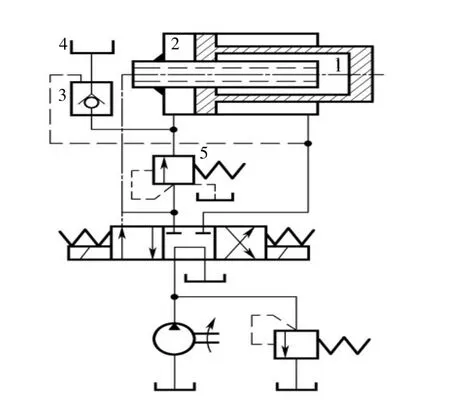
图1 增速液压缸增速回路

2 仿真分析

2.1 仿真模型的建立

根据液压缸增速回路工作原理[3-5]，利用AMESim软件搭建的回路仿真模型如图2。

图2 增速回路AMEsim仿真模型

利用AMESim软件中BAP11（12）模块模拟增速液压缸的小腔1，BRP18模块模拟增速液压缸的大腔2；其余模块模拟增速回路中的各种开关及阀体。

2.2 参数设置

根据增速回路工作原理及元件实际参数，设定各模块参数如表1。

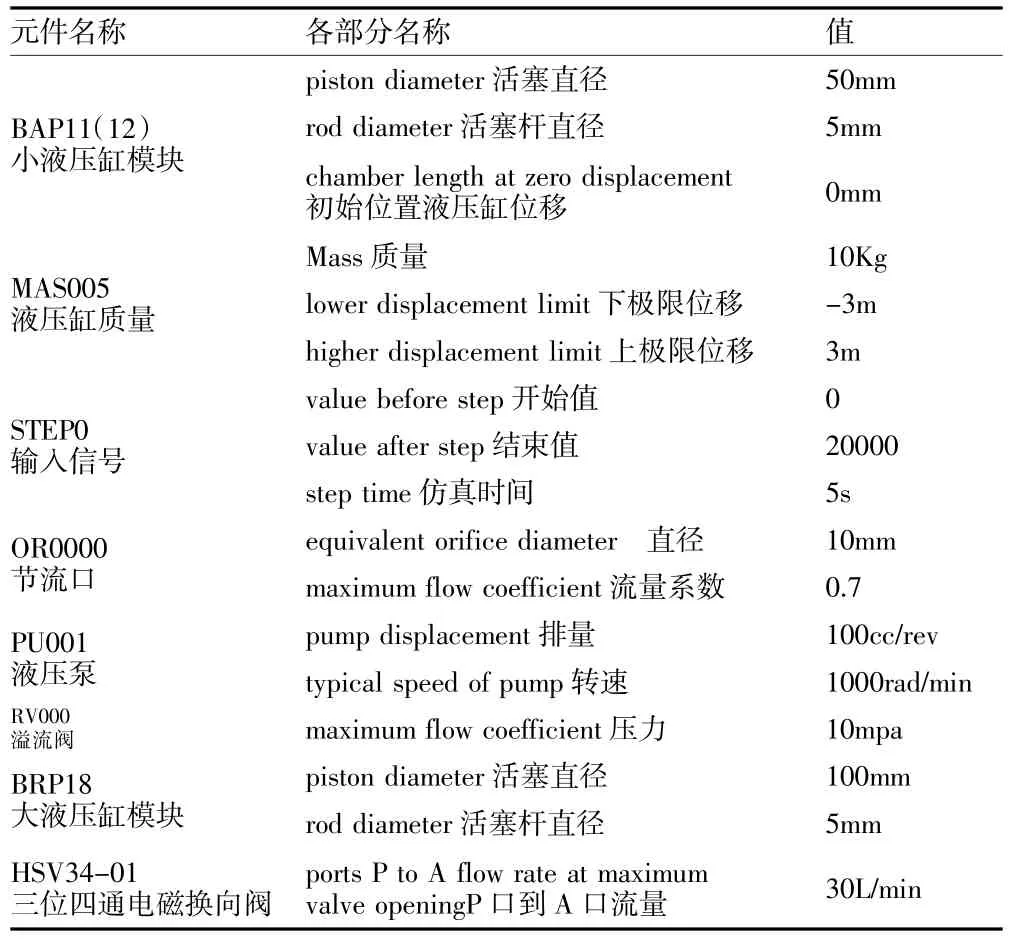
表1 参数设置表

其他子模型参数保持系统默认值。

2.3 仿真结果分析

图3为增速液压缸增速回路进程中液压缸速度随时间变化的曲线图：在仿真区间1～5 s中，由于外加负载为零，此时顺序阀处于关闭状态，液压泵泵出的油液经管道进入液压小缸中，液压缸以0.318 991 1 m/s的速度向右运行；在仿真时间为5 s时，外加负载为20 000 N的作用力由STEP0提供并加人液压回路当中，此时顺序阀入口处的压力瞬间达到22.65 MPa，超过了其设定的开启压力10 MPa，顺序阀打开。此时液压泵泵出的压力油进顺序阀流经大液压缸，由于液压缸面积增大，液压缸的速度减小，在本文中设定的参数下，液压缸的速度最终稳定在0.255 155 5 m/s的速度下运动。这与理论推导得出基本一致，说明了仿真模型的正确性。

但在仿真结果图中可以发现，在仿真时间为5 s时即刚刚加入外加负载之后，增速液压缸的速度出现了震荡：震荡的最低值达到了-0.387 m/s，最高值达到了0.689 m/s，速度变化量绝对值达到1.076 m/s，且震荡时间维持了将近1 s。这对于液压系统来说，危害巨大，特别是对于高精度的液压系统，尤为明显。

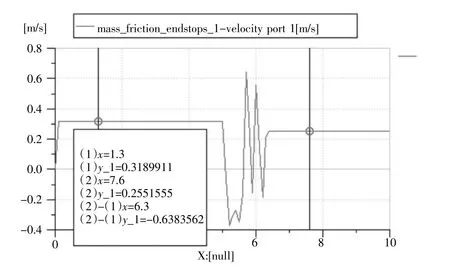
图3 增速液压缸进程速度变化曲线

下面对系统进行优化，通过在增速液压缸进油口处增加一个节流阀方法来减小液压缸的震荡幅度及震荡时间。研究得到节流口优化参数，为增速液压缸增速回路的设计提供参考依据，改进的仿真回路如图4所示，在增速液压缸进油口处增加一个节流阀。

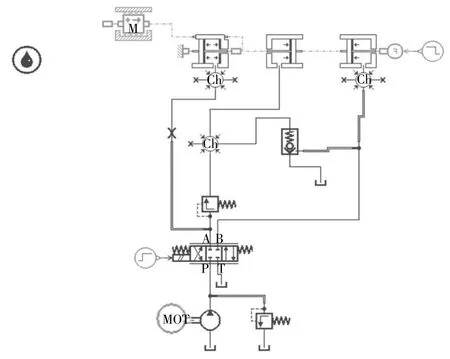
图4 改进的增速回路AMEsim仿真模型

如图4改进的的增速缸增速回路中，采用节流模型OR0000来模拟回路中小液压缸的进油口，通过子模型OR0000可以来设定不同的进油直径大小，以获得在不同参数工况下增速液压缸的动态特性。

通过OR0000设定进油口的直径为10 mm，获得的增速液压缸的速度变化曲线如图5所示。

从图5的仿真结果可以发现，在小液压缸直径为10 mm下有：在仿真区间1～5 s中，液压缸的运动速度为0.314 063 1 m/s；在仿真时间为5 s时，外加负载为20 000 N的作用力由STEP0提供并加人液压回路当中，液压缸的速度最终稳定在0.255 100 5 m/s。速度大小与原仿真模型获得的液压缸速度大小基本一致。

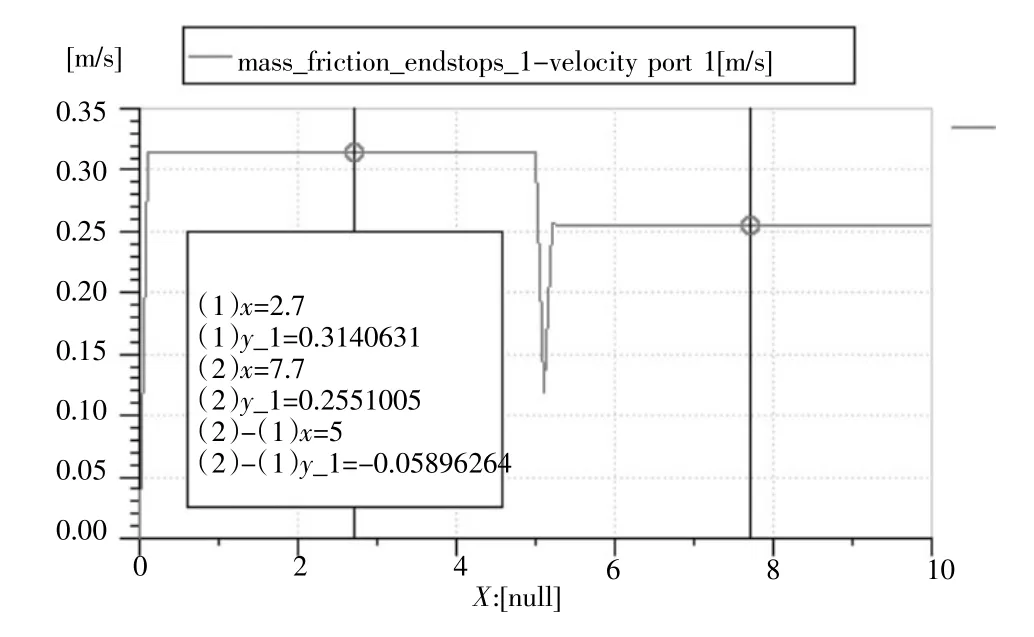
图5 改进的增速缸速度随时间变化曲线

但相对于原仿真模型，在仿真结果图中可以发现，在仿真时间为5 s时即刚刚加入外加负载之后，增速液压缸的速度现震荡情况已经消失：只是在负载加入的瞬间，由于液压泵的压力油没有及时补充至液压缸，致使液压缸的速度瞬间降低到0.102 35 m/s。但液压系统在约为0.1 s的时间内恢复到了液压缸的稳定速度值0.255 100 5 m/s。这比原仿真模型的1 s时间大大减少。

以上结论得出，适当的调节小液压缸进油口出的直径及长度可以减轻增速回路在速度变化瞬间速度的不稳定性，下面通过改变OR0000值的大小，对模型进行批处理仿真：分别取equivalent orifice diameter值为 9 mm、9.5 mm、10 mm、10.5 mm、11 mm，五组组数据来获得在此工况下增速回路的最佳入口直径的数值大小。

图6（a）为直径大小分别为9 mm、9.5 mm下液压缸速度变化曲线图，从仿真结果图可以发现，当小孔直径由9 mm增加到9.5 mm时有：在仿真区间1～5 s中，液压缸的运动速度由0.270 028 6 m/s增加到0.293 061 6 m/s；在仿真时间为5 s后，两者液压缸的速度最终分别稳定在0.255 100 3 m/s、0.255 100 4m/s。在加入负载的瞬间，对于前者，液压缸的速度震荡剧烈，出现了时高时低的反复震荡的情况。

图6（b）为直径大小分别为9.5 mm、10 mm下液压缸速度变化曲线图，从仿真结果图可以发现，当小孔直径由9.5 mm增加到10 mm时有：在仿真区间1～5 s中，液压缸的运动速度由0.293 061 6 m/s增加到0.314 061 3 m/s；在仿真时间为5 s后，两者液压缸的速度最终分别稳定在0.255 100 4 m/s。在加入负载的瞬间，随着小孔直径增加，液压缸的速度震荡进一步降低。

图6（c）为直径大小分别为10 mm、10.5 mm下液压缸速度变化曲线图，从仿真结果图可以发现，当小孔直径由10 mm增加到10.5 mm时有：在仿真区间1～5 s中，液压缸的运动速度由0.314 061 3 m/s增加到0.318 991 1，这与原仿真模型中获得的该阶段的速度大小一致；在仿真时间为5 s后，两者液压缸的速度最终分别稳定在0.255 170 4 m/s、0.255 166 8 m/s。在加入负载的瞬间，随着小孔直径增加，液压缸的速度震荡弧度进一步降低，但可以发现，随着孔径的进步增加，液压缸达到稳定速度的时间略有增加。

图6（d）为直径大小分别为 10.5 mm、11 mm下液压缸速度变化曲线图，从仿真结果图可以发现，当小孔直径由10 mm增加到10.5 mm时有：在仿真区间1～5 s中，两者液压缸运动速度都稳定在0.3 189 911 m/s，这与原仿真模型中获得的该阶段的速度大小一致；在仿真时间为5 s后，两者液压缸的速度最终分别稳定在0.255 166 8 m/s 0.255 015 2 m/s。在加入负载的瞬间，随着小孔直径继续增加，液压缸的速度震荡弧度反而开始增加。

通过对不同节流口直径下液压缸速度变化进行了仿真研究，得到了本设计工况下较优的节流口直径值为10～10.5 mm，为增速回路的设计、结构参数的优化及元件选型有一定参考价值。

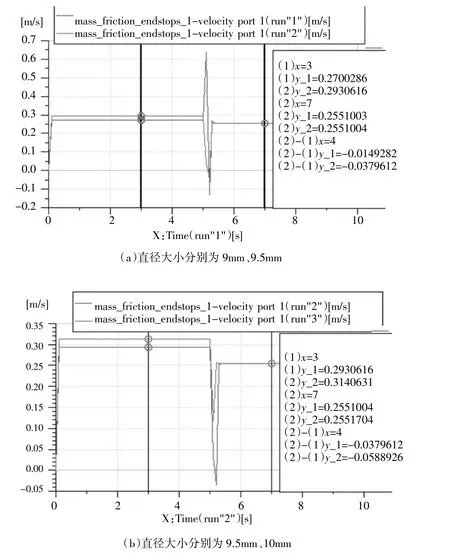
图6 不同节流口直径下液压缸速度变化曲线

3 结束语

本文基于AMEsim建立了增速液压缸回路仿真模型，分析了回路压力、速度的稳定性，得到了其速度变化特性曲线；对模型进行优化设计，得出在本文工况下，进油口直径在10～10.5 mm之间时，该增速回路能获得较好的速度动态性能，为增速回路的精度及理论深度提高提供了理论依据。