提升思维能力 加强数学应用——2020年高考山东物理卷压轴题评析与教学思考

徐忠平

(山东省招远第一中学，山东 招远 265400)

1 试题重现

原题.如图1所示,一倾角为θ的固定斜面的底端安装一弹性挡板,P、Q两物块的质量分别为m和4m,Q静止于斜面上A处.某时刻,P以沿斜面向上的速度v0与Q发生弹性碰撞．Q与斜面间的动摩擦因数等于tanθ,设最大静摩擦力等于滑动摩擦力.P与斜面间无摩擦,与挡板之间的碰撞无动能损失,两物块均可以看作质点,斜面足够长,Q的速度减为0之前P不会与之发生碰撞,重力加速度大小为g．

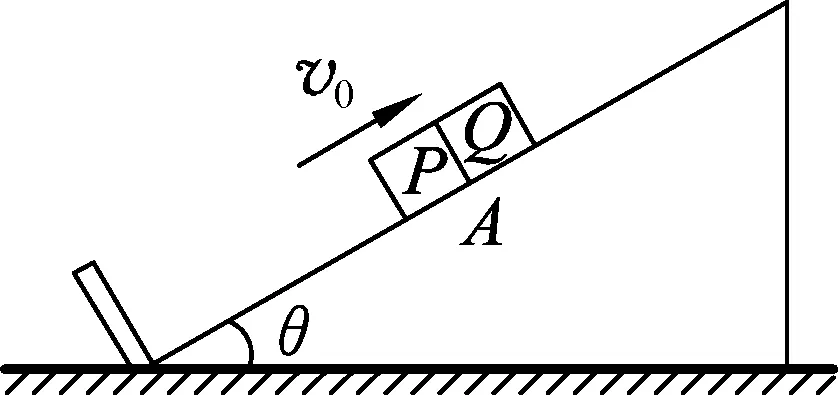
图1

(1) 求P与Q第一次碰撞后瞬间各自的速度大小vP1、vQ1;

(2) 求第n次碰撞使物块Q上升的高度hn;

(3) 求物块Q从A点上升的总高度H;

(4) 为保证在Q的速度减为0之前P不会与之发生碰撞,求A点与挡板之间的最小距离s．

命题意图:本题考查了完全弹性碰撞中动量与能量观点的应用,同时考查了应用牛顿第二定律与动力学观点解题的能力,需要考生有较强的逻辑思维能力与严谨性．本题渗透了较多数学知识,需要考生具有扎实的数学基础,同时考验了考生的计算能力．

试题特点:本题应用了高中物理教学中常见的几个模型:完全弹性碰撞模型、斜面模型等．题目整体解题思路容易寻找,但对考生思维能力要求较高,需要考生有清晰的逻辑与严谨的推理计算才能将其正确解出,计算量较大．

2 解题中的数学思维方法

(1) 求P与Q第一次碰撞后瞬间各自的速度大小vP1、vQ1.

该问考查完全弹性碰撞模型,以P的初速度方向为正方向.

由动量守恒定律得

mv0=mvP1+4mvQ1.

(1)

由机械能守恒定律得

(2)

联立(1)、(2)式解得

(3)

(4)

(2) 求第n次碰撞使物块Q上升的高度hn.

解法1：数学归纳法.

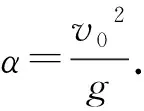
设第1次碰撞后Q上升的高度为h1，对Q由运动学公式得

(5)

联立(1)、(2)、(5)式得

(6)

设P运动至与Q刚要发生第2次碰撞前的位置时速度为v02，第一次碰后至第2次碰前，对P由动能定理得

(7)

联立(1)、(2)、(5)、(7)式得

(8)

P与Q的第2次碰撞，设碰后P与Q的速度分别为vP2、vQ2，第2次碰撞后Q上升的高度为h2,P运动至与Q刚要发生第3次碰撞前的位置时速度为v03,理同第一次碰撞得

(9)

(10)

(11)

(12)

P与Q的第3次碰撞:设碰后P与Q的速度分别为vP3、vQ3,第3次碰撞后Q上升的高度为h3，同理得

(13)

(14)

(15)

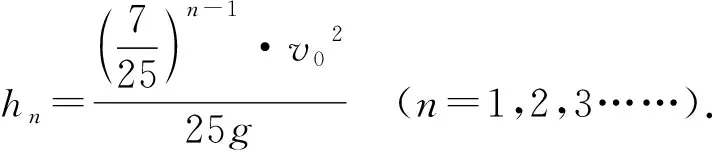
该方法通过计算前几次碰撞后物块Q上升的高度，得出物块Q上升的高度成等比数列，最终求出hn.或者也可根据物块P碰前速度的等比关系求出第n次碰撞前物块P的速度，再通过物块P碰前速度与物块Q碰后上升高度的关系求解物块Q第n次碰撞后上升的高度,相对而言计算量较少.而该方法思维方法较为简便，计算量较大，较为耗费时间且对考生计算能力要求较高..

解法2：递推公式法.

设第n次碰撞后物块P的速度为vPn，物块Q的速度是vQn,第n次碰前物块P的速度为vn.

对物块P、Q第n次碰撞，由动量守恒定律得

mvn=mvPn+4mvQn.

(16)

由机械能守恒定律得

(17)

联立(16)、(17)式得

(18)

(19)

对物块P从第n-1次碰撞位置到第n次碰撞位置，由动能定理得

(20)

对物块Q第n次碰撞后到静止，由动能定理得

(21)

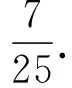
(3) 求物块Q从A点上升的总高度H.

解法1：等比数列求和公式.

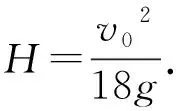
解法2：动能定理法.

当P、Q达到H时，两物块到此处的速度可视为0，对两物块运动全过程由动能定理得

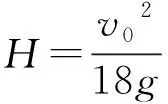
对于本题来说，由于第2问中需要求解hn，得到hn为等比数列，故在第3问中需要求H.即hn的和时，使用等比数列求和公式是较为自然的思路，运算量较小，容易得到正确结果，而若是使用动能定理法，可能有些考生由于思维不够严谨，对物块Q上升H后两物块所处的运动状态分析不清，导致出现错误.若是没有第2问的铺垫，直接求解物块Q上升的高度，则认真对两物块的最终运动状态进行分析，再使用动能定理法更为简便.

(4) 为保证在Q的速度减为0之前P不会与之发生碰撞，求A点与挡板之间的最小距离s.

由分析可得，随着碰撞次数增加，碰后物块Q的速度减小，减速到0所用时间减少，而物块P距离底部挡板距离增大，碰后速度减小，返回至斜面上与物块Q碰撞所用时间增大，故要使物块P在物块Q的速度减为0之前不会与之发生碰撞，只需第1次碰撞后在物块Q的速度减为0之前物块P不会与之发生碰撞.

设Q第1次碰撞至速度减为0需要的时间为t1，由运动学公式得vQ1=2gt1sinθ.设P运动到斜面底端时的速度为v，需要的时间为t2，由运动学公式得

v=vP1+gt2sinθ，v2-vP12=2gsinθ.

设P从A点到Q第1次碰后速度减为0处匀减速运动的时间为t3，

v02=(-vP1)-gt3sinθ.

当A点与挡板之间的距离最小时，

t1=2t2+t3.

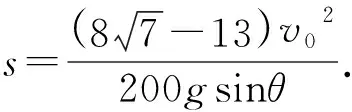
3 教学思考与启示

3.1 重视模型

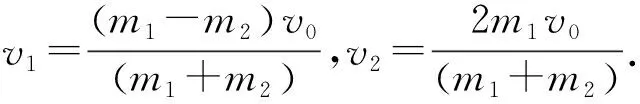
3.2 培养对多物体多过程题目的分析能力

本题涉及两个物块，碰撞、匀变速直线运动等多个过程，需要理清物块在不同位置不同时刻的速度、受力、运动状态，容易出现在某个过程有些点没有注意或重复计算、受力状态分析不清、相对空间位置混乱等问题.为此，需要培养学生条理分析每个过程的能力，养成每个状态画受力分析图、相对位置关系图的习惯，减少受力分析时出现的错误，使各个物体之间的相对位置关系更加清晰、直观.同时规范符号的角标，明晰其代表的含义，规范思路的严谨性.

3.3 培养一道题研究多种解法的习惯

高考是限时答题，考生在平时的训练中不应只满足于会做题，而应当在已经解出答案的基础上继续思考：是否能从另外的角度入手解题，哪种观点更适合用于解决该类问题，如何能够更加快捷地解出这个问题，如果换了问题的问法是否另一种方法就会变得简便.只有在平常的训练中保持这样思考的习惯，才能在考试时迅速地找到解决方法，迅速且准确地解决问题，有足够的时间完成有能力解决的题.

3.4 加强数学知识的应用

在高中物理教学中，要培养学生将数学方法与物理思维有机融合的能力，需要做到两点：一是对初高中所学数学知识熟练掌握，在教授学生时，引导学生使用某些数学方法，而不是对涉及到数学知识的部分避而不谈；二是培养学生从物理问题中抽象出数学问题的能力，在求解物理问题时，使用物理规律将各物理量间的关系列出后，然后利用函数、方程等数学知识求解，将物理问题转化为数学问题.如2020年山东高考物理题的第18题(2)便是利用动能定理，动量守恒，机械能守恒等规律列出各物理量间规律，然后运用数学知识得出hn与hn-1间的递推公式，从而求解.

在物理的学习中，数学是必不可少的一样工具，但数学在物理中的应用，并不只限于数据的计算与处理，还包括运用数学中的公式定理对运算进行简化，使用学到的数学知识从另一个角度更加简便地解决物理中的难题，将学习数学时的思维方法迁移到物理的学习中，另辟蹊径，找到更加简单的解题方法.

例题.一简谐横波沿x轴正向传播，图2(甲)是t=0时刻的波形图，图2(乙)是介质中某质点的振动图像，0时刻该质点的振动位移为-0.1 m，2 s在平衡位置处，则波的传播速度为

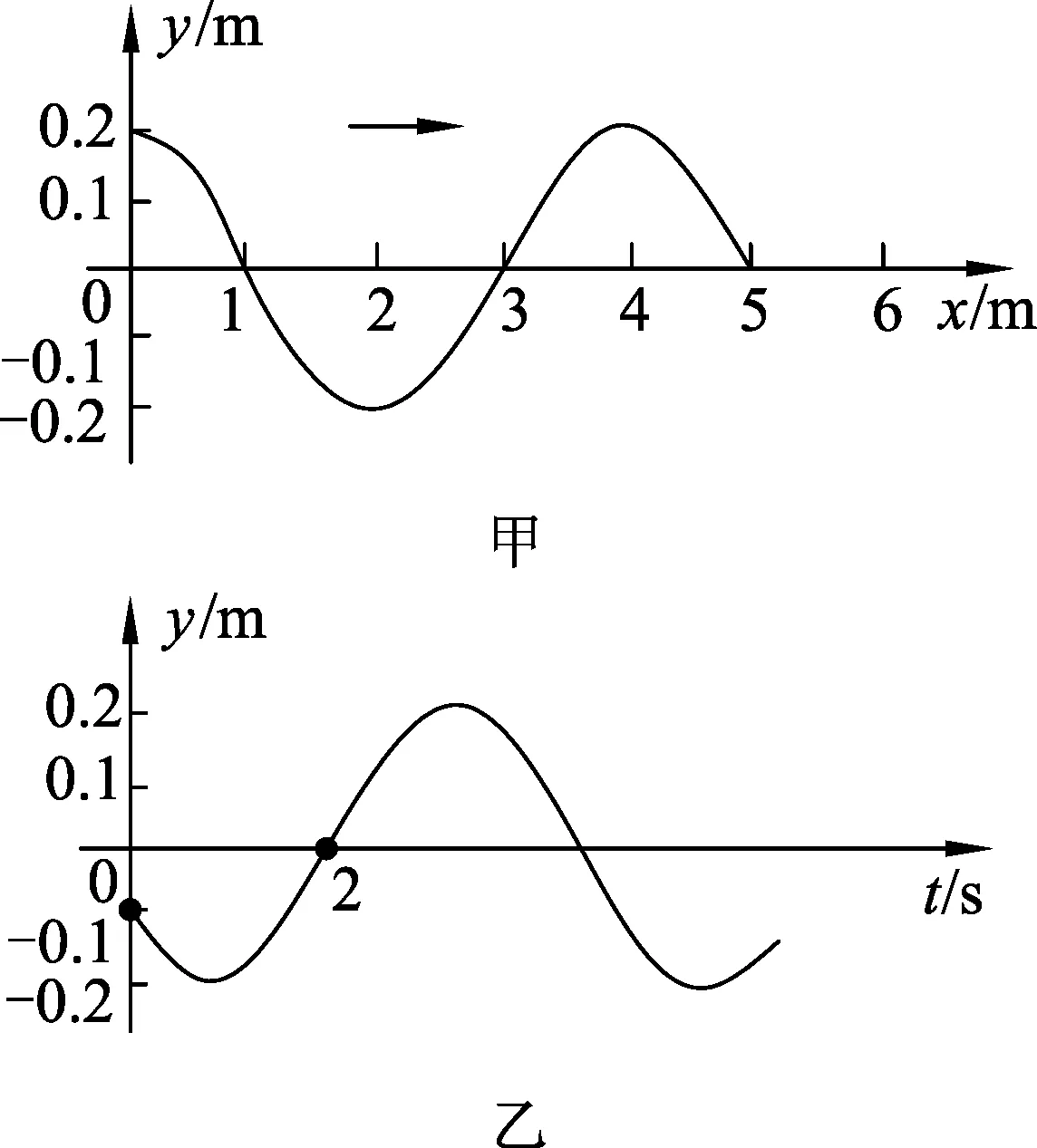
图2

(C) 0.8 m/s. (D) 1.5 m/s.