论熵的定义与熵的物理意义

邢红军

(首都师范大学教师教育学院，北京 100048)

在热力学乃至整个物理学中，熵都称得上是一个很重要的物理概念.它对于透彻理解和深入掌握热力学第二定律，甚至是了解物质世界的演化过程都有着非常重要的作用.由于熵的概念比较抽象，一直以难懂而闻名于世.美国著名物理学家P.W.Atkin也说：科学对解放人类精神的贡献没有任何部分像热力学第二定律那样大，同时科学的其他部分也几乎没有这样高深莫测.”他称熵是“永远难以透彻了解的.”可见熵的概念确实是不易理解的，对初学者尤其如此.

为了确切了解熵的定义和深入理解熵的物理意义，本文先对熵的定义与熵的物理意义研究现状进行综述，而后在对熵的研究过程中，采用“两步走”的方法，即把熵的定义的研究与熵的物理意义的研究分开，避免将二者混在一起进行研究.先从“能量分布”的角度研究熵的定义，而后再从“能量做功”的角度研究熵的物理意义.

1 “熵”的定义与熵的物理意义研究现状

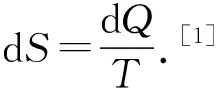
自克劳修斯提出熵这一概念后,150多年来,“熵问题的讨论已波及信息论、控制论、概率论、天体物理、宇宙论、生命与社会等多个不同领域．由于自然界存在的复杂性,使熵的定义出现了极大的混乱,各种议论概念含糊、问题矛盾多多．[2]”究其原因,正是对经典热力学中“熵”的定义缺乏准确理解所致．

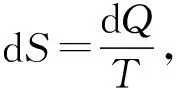
对于熵的理解,只从微观层次上解释熵对于人们认识熵的物理本质还是不够的．著名物理学家吴大猷先生曾指出:“熵的观念是很复杂很深的,很多书为了方便,只从统计观点来解释熵,虽不说这是错,但这是不够的．”[4]因为对于一些研究人员或工程师来说,他们更关心熵的宏观应用．例如用熵来描述热机的热功转换效率,分析热传递过程的不可逆性等．而且,即使已有“熵是系统混乱程度的度量”这一微观物理意义的解释,也似乎没有减少熵的神秘色彩．正如我国著名物理学家冯端所说,“熵是一个极其重要的物理量,但却又以其难懂而闻名于世．”[5]赫尔曼.哈肯也曾指出:“在涉及到熵这一概念时,物理学家们本身也存在着相当的混乱．”[6]就连以熵作为主要研究内容之一并获得诺贝尔化学奖的科学家普利高津都认为,“熵是一个很奇怪的物理量,不可能给出一个完备的解释．”[7]而从下面这个有关信息熵的有趣故事中,更能够深刻体会到科学家们对于熵概念难懂的无奈．1948年,贝尔实验室的电气工程师申农(Claude Shannon)在研究通讯信号时,提出了一个表征“丢失的信息(lost information)”或“不确定度(uncertainty)”的物理量,但他一直苦于找不到合适的名字来命名该物理量．一次偶然的机会,申农遇到了冯·诺依曼(John Von Nouma)并向他请教这个问题．冯·诺依曼说:“为什么不叫它熵呢?一方面它和统计熵的数学表达式很相像,但最重要的一点是,现在根本就没有人知道熵是什么,因此取名熵别人也不会提出反对．”[8]

那么熵的物理学意义究竟是什么呢?成如山认为,“熵是一个像体积、压强、温度、内能那样真实的物理量”,“正如温度是系统分子热运动剧烈程度的量度、气体压强是大量分子碰撞器壁强度的量度一样,熵的物理意义应该是构成系统的微观粒子热运动混乱程度量度”．[9]这种对熵物理意义的认识正如吴大猷先生所指出的那样,是只从统计观点来解释熵,显然并没有触及到熵的本质．赵凯华等人认为,热量从高温传到低温熵增加意味着能量的分散和退降,即把熵看作是能量退化贬值的量度．[10]这种对熵物理意义的理解是从能量退降的角度出发的,但并不能从熵的表达式中直接得出熵的物理意义,所以,也不能认为是熵的一个满意的定义．也有研究者提出,“熵是表示任何一种能量在空间分布均匀程度的物理量．”[11]这一定义已经比较接近熵概念的本质了,但也并不是熵概念的全部,而且也不能从熵的表达式中直接得出．

纵观对熵的定义与熵的物理意义的探讨,不难发现,人们从不同角度对熵的定义与物理学意义做了解释,均有其合理之处．然而,这些解释都是间接或内隐的,无法给人一目了然之感,因此,对认识熵的定义与熵的物理意义就产生了严重障碍．

我们认为,人们之所以长期以来觉得熵的概念难以理解,归根结底是因为一个关键问题没有搞清楚,即:熵的定义应当从“能量分布”的角度进行定义,而熵的物理意义则应当从“能量做功”的角度进行定义．不能将二者区分而将两者混淆在一起讨论,是导致熵的概念艰涩难懂的重要原因．

2 “熵”的定义

在确立上述观点的基础上,我们从熵的原始定义式出发,借助一种重要的科学方法——比值定义法,通过剖析熵的定义式中物理量的深层含义,尝试从“能量分布”的角度对熵的定义给出符合熵概念本质的解释．

在熵定义式的分子上,dQ表示热量,它是能量的一种,这是易于理解的．因此,要想真正理解熵的定义,就必须对定义式中分母T的深层含义进行剖析．

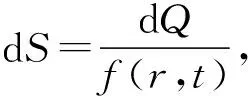
从能量分布或能量储存的角度讨论熵的定义,不难理解,要使一个系统以做功的形式向外输出能量,该系统必须与外界有能量密度的差异．只有存在这种差异,能量才会自动地从高密度区域流向低密度区域,直到能量密度的差异消失为止．换句话说,我们只能从能量的流动过程中得到功．例如,水从高处流向低处推动水轮机而做功,热量从高温物体流向低温物体推动热机而做功,都是能量密度从非均匀分布趋于均匀分布的结果．能量分布越不均匀,熵就越小,反之熵就越大．如果能量分布完全均匀,熵值就达到最大．这时就不可能再发生能量从这一区域自发转移到另一区域的宏观流动,也就是不再对外做功．除非由于外界的原因,再度造成能量密度的不均匀,才能形成能量的流动,从而可以对外做功．由此可见,熵可以作为系统能量储存在空间均匀程度的一种量度．

3 “熵”的物理意义

如前所述,经过长达一个半世纪的探讨,有的学者利用微观统计学的方法对熵的物理学意义进行解释,有的学者从能量退化贬值角度对其进行阐述,还有的学者从能量分布视角进行说明．至今为止,对熵的物理意义的认识仍在继续探究．

我们认为,在熵的定义研究的基础上,从“能量做功”的角度可以给出熵的物理意义的解释．

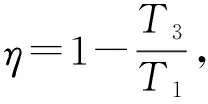
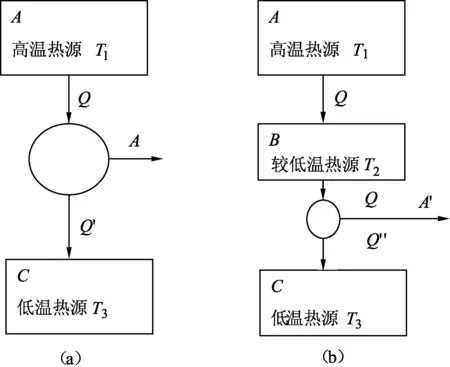
图1

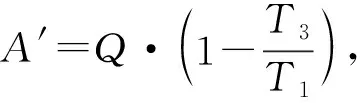
不难发现,熵的物理意义是:它是作为能量的不可使用程度的一种量度．这是因为,在一切实际过程中,能量的总值虽然保持不变(能量守恒),但能量可以利用的程度却随着熵的增加而降低了．换句话说,从能量的数量上说,能量的总量保持不变,而从能量的品质上说,品质变差了,可以用来做功的部分变少了．也可以说,能量的价值降低了．从以上分析可以知道,储存于高温下的热量,能够对外做较多的功,也就是具有较好的品质．储存于低温下的热量,同样数量的热量却只能对外做较少的功,因为其品质较差,故称其为贬值的能量．