析说滚动摩擦力
周启勇
(深圳中学,广东 深圳 518000)
在教学中有学生甚至教师对滚动摩擦力只停留中的教材中“滚动摩擦力小于滑动摩擦力”,那滚动摩擦力到底有何特点?它的大小、方向又如何?本文通过几个例题的分析,逐步析说滚动摩擦力.
1 刚体滚动运动时的摩擦力
1.1 当刚体纯滚动中时,静摩擦的大小与方向的判断

图1
例1.质量为m、半径为R的匀质实心圆柱体,受一水平向右的力F的作用下,在水平面上作纯滚动,力F的作用线到质心转轴的垂直距离为r,如图1.

说明:刚体纯滚动时的静摩擦力的大小不仅同拉力F有关, 还与圆柱体的半径R以及圆心到水平力F作用线的垂直距离r有关. 当R、r为定值时, 静摩擦力同水平外力F成正比.
讨论: (1) 当F=0时,f=0,圆柱体不受静摩擦力,圆柱体靠惯性运动.

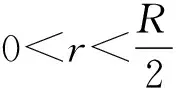

由此可知,刚体纯滚动时,静摩擦的大小与方向要视情况来定,基本方法是列动力学方程求解.
1.2 刚体有滑滚动摩擦力方向的确定

图2
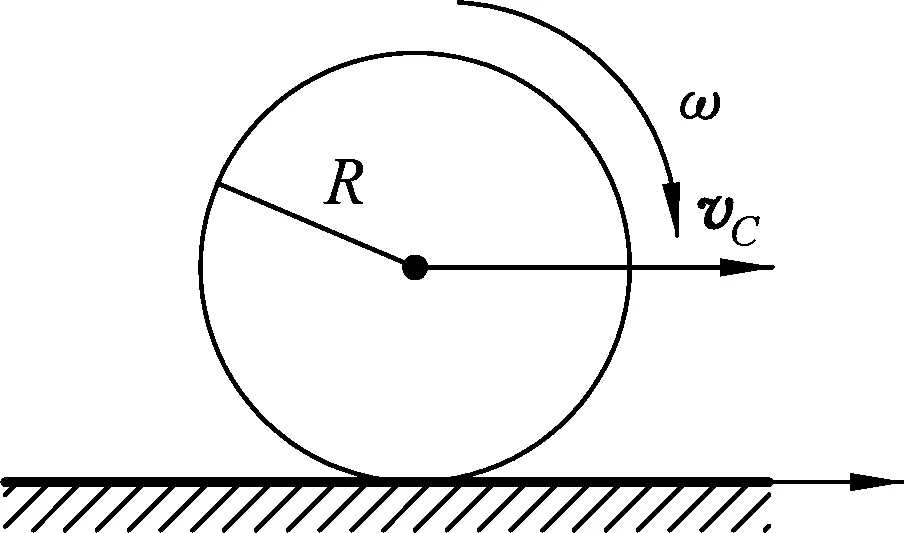
例2.当刚体在滚动中有滑动运动时,摩擦力实为滑动摩擦力,方向与“相对运动”的方向相反.设有一底面半径为R的均匀圆柱体,质心的平动速度为vC,绕质心转动的角速度为ω,如图2所示.
讨论:
(1) 如果Rω>vC,则圆柱体最低点有与vC方向相反的滑动.滑动摩擦力f方向与相对运动方向相反,则f方向与vC相同;大小由滑动摩擦力公式得f=μN.
(2) 如果Rω (3) 如果Rω=vC,则圆柱体最低点有与vC方向没有相对滑动,即纯滚动,没有相对运动,如果有摩擦力,实为静摩擦力. 图3 例3.设圆柱体由静止开始沿水平面作纯滚动,外力F与作用于圆心O点且水平,当运动距离为s时,速度达到v,角速度为ω,如图3. 解析:此时转动动能为 则质心的平动动能 因此圆柱体总能量 若假设在平面光滑情况下,运动相同的位移,圆柱体只平动不转动,总动能等于力F所做的功 由此说明有、无静摩擦力总能量相等,说明静摩擦力不改变其总能量, 即静摩擦力不做功.但静摩擦力又使圆柱体产生了绕质心转轴的转动动能,所以静摩擦力作用只是将平动动能转换成转动动能. 图4 例4.如例1中,如做初状态Rω f=μN=μmg. 动力学方程 运动学方程 vC=v0+at;ω=ω0+βt. 图5 其中负号表示滑动摩擦力对圆柱体做负功, 即圆柱体的动能减少. 例5.如例1中,如做初状态Rω>vC的有滑滚动,滑动摩擦力f方向与vC相同,如图5最开始时,vC=v0,ω=ω0,则t时刻时,有摩擦力 f=μN=μmg. 动力学方程 运动学方程 vC=v0+at;ω=ω0+βt. 物体将保持质心速度及转动的角速度恒定的纯滚动.由动能定理 其中负号表示滑动摩擦力对圆柱体做负功, 即圆柱体的动能减少. 一般滚动摩擦是一个物体在另一物体上滚动或有滚动趋势时,接触面处产生的不对称形变引起的一种阻碍滚动的作用,如图6,向右滚动时,接触面处产生的凸出来的形变. 图6 例6.如图6所示,假定水平面上的圆柱体在外力F作用下匀速无滑滚动,重为G, 半径为R, 在这一过程中, 圆柱体除受到重力、弹力外,在接触处还受到滚动摩擦力f滚. 在竖直方向, 重力G和弹力N构成一对平衡力,在水平方向f滚.滚动摩擦实际上是一种阻碍滚动的力矩.它的产生是由于圆柱体与地面接触处的形变所引起的. 解析:G与N构成力偶矩,因匀速β=0,则合力矩∑M=0. 讨论:刚性越好的物体Δx越小,而刚体Δx=0.我们骑自行车时,车胎气越足,刚性越好,f滚越小;气越少,刚性越差,f滚越大.当自行车驶入沙坑时,Δx增大,f滚越大,阻力增大.1.3 纯滚动时静摩擦力做功问题


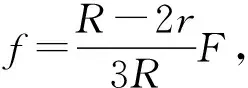
1.4 有滑滚动时摩擦力做功问题





2 一般物体滚动运动时摩擦力




