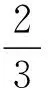对竖直倒下匀质杆内部弹力的研究

涂德新

(江西师范大学附属中学，江西 南昌 330046)

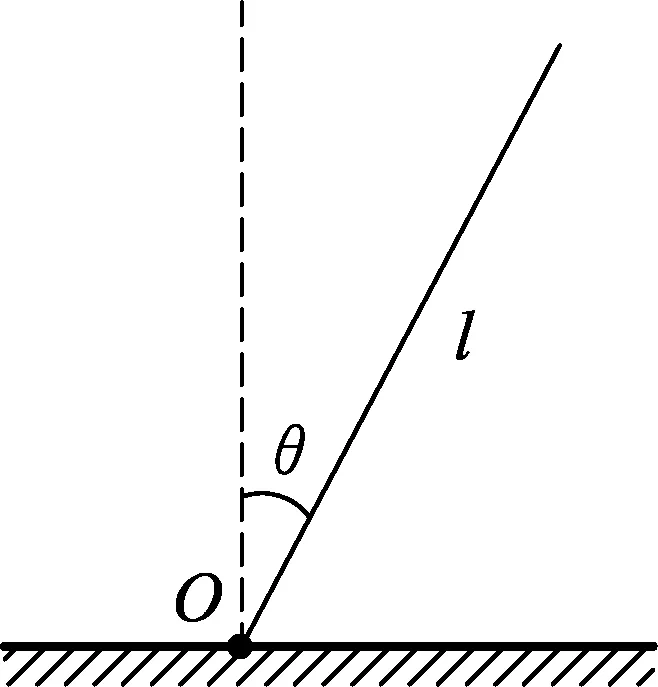
图1

质量均匀分布的重杆是一个重要的物理模型,匀质杆在受力时的形变比较复杂,可能会有拉伸(压缩)形变,对应于法向力;也可能有剪切形变,对应于切向力;还可能有弯曲形变,对应于力偶矩．很多参加物理竞赛的同学包括部分教师在分析匀质杆的转动问题时往往会忽视杆内部力偶矩的存在,进而得出矛盾的结果．下面建立一个模型来处理此问题．参数设定:匀质杆长度为l,质量为m,以下端O为转轴,最初竖直,某时刻转到与竖直方向的夹角为θ,如图1所示,不考虑空气阻力的作用,重力加速度为g,研究杆内部作用力的分布．

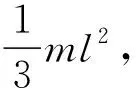
可以求得

(1)

对杆相对转轴O运用转动定律

可以求得

(2)

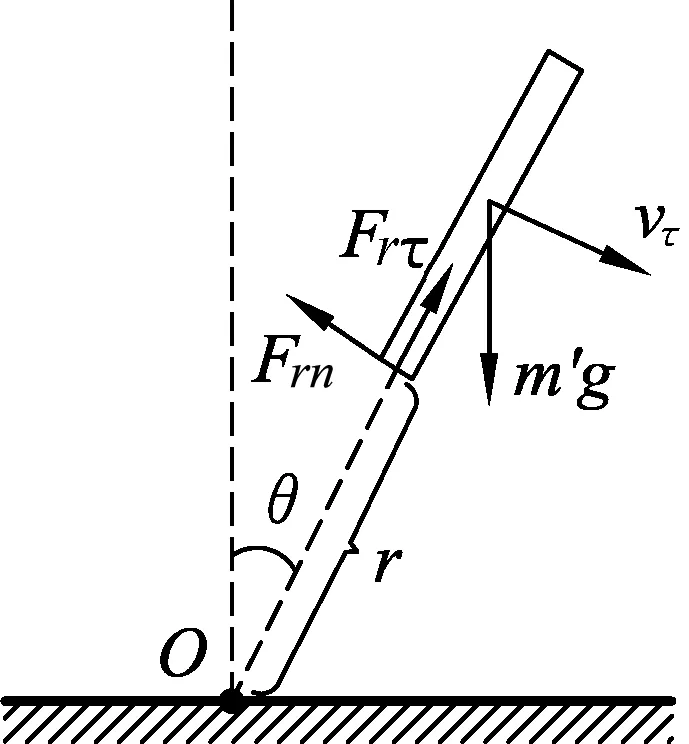
图2

如图2所示,研究从离转轴r处到l处杆的运动,应该是质心的平动和绕质心的转动,其质量

(3)

这段杆的质心绕下端的转轴O在做加速圆周运动,可以写切线方向和法线方向的牛顿第二定律来求切向力和法向力．

设r处相互作用的切向力为Frτ,可得

(4)

由(2)-(4)式可以求得

(5)

这个力就是r处剪切形变对应的切向力．

设r处的相互作用的法向力为Fr n,可得

(6)

由(1)、(3)、(6)式可以求得

(7)

这个力就是r处压缩形变对应的法向力．

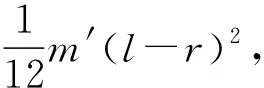
(8)

将(2)、(3)、(5)式求得的相关参量代入(8)式后发现等式两边不相等.这是很多学生和教师感到困惑和矛盾的地方．下面解决此问题．

仔细研究后发现,这是物理模型出了问题,不能把杆看成细杆,杆应该有不能忽略的截面．换句话说Fr n这个法向力是一个分布力,如图3所示,杆沿截面的压缩并不均匀,也就是说有弯曲形变.分析后发现可能截面的上侧为

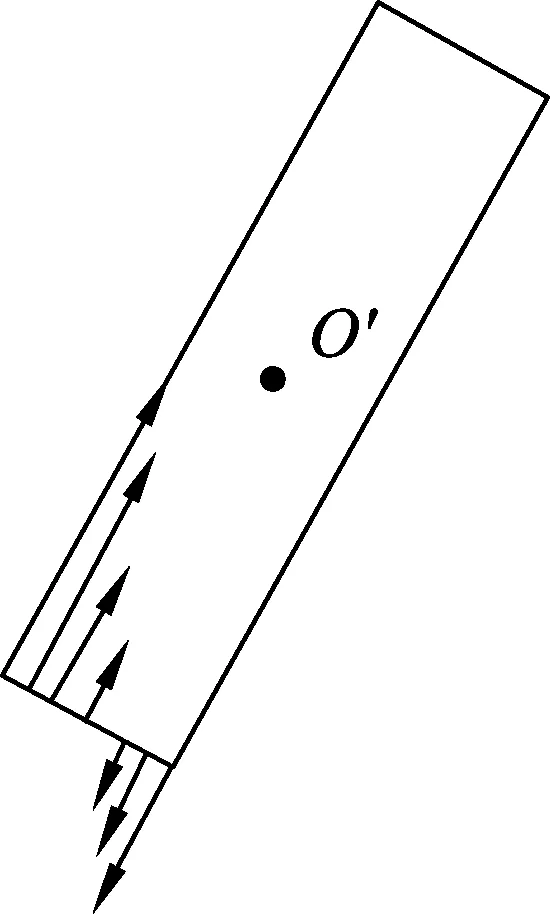
图3

压缩形变,下侧为拉伸形变,于是沿杆的这些分布力可以这样处理:最上侧和最下侧的两个力方向相反但大小不等,可以处理为沿杆向上的微元应力和一个顺时针的微元力偶矩,上下侧对称处的力都可以这样处理,最后所有的微元应力可以合成为沿杆向上的应力Fr n,所有的微元力偶矩可以合成为顺时针的力偶矩Mr,Fr n上文已经求出,下面求解力偶矩Mr．

考虑到杆内部有力偶矩后,(8)式有误,应该修正．对杆的上端以其质心O′为轴列转动定律:

(9)

由(2)、(3)、(5)、(9)式可以求得

改写为

(10)