用字典排列法解答的一道改编题

甘志国

(北京市丰台二中 100071)

基金项目：本文系北京市教育学会“十三五”教育科研滚动立项课题“数学文化与高考研究”(课题编号FT2017GD003，课题负责人：甘志国)阶段性研究成果之一.

改编题(由普通高中课程标准实验教科书《数学·选修2-3·A版》(人民教育出版社2009年第3版)第41页第2题改编)用数字0,1，2，3，4，5组成没有重复数字的六位数，问：

(1)其中有多少个是奇数？

(2)其中有多少个大于201345？

(3)其中的320514是从小到大排列的第几个数？

(4)其中从小到大第300个数是几？

(5)其中从大到小第300个数是几？

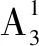
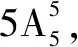
综上所述，可得所求答案是321540.

综上所述，可得所求答案是324015.

注这道改编题的解法就是字典排列法.

下面这道类题的解法也是字典排列法.

类题[1][2](2013年华约自主招生数学试题第1题)已知集合A={x|x≥10,x∈N},B⊆A，且B中的每个元素同时满足：(a)各数位上的数字互不相同；(b)任意两个数位上的数字之和不为9.求：

(1)B中有多少个两位数？多少个三位数？

(2)B中是否有五位数？是否有六位数？

(3)将B中的元素从小到大排列后，第1081个元素是多少？

解将0,1,2,…,9中和为9的数字两两配成5对：(0,9),(1,8),(2,7),(3,6),(4,5).

得B中的元素不能同时含有上述一对数字中的两个数字.

(1)对于B中的两位数：十位数字有9种选法(可选1,2,…,9)；十位数字选定后，个位数字有8种选法(与十位数字不同，且不能是上面配对的数).所以B中的两位数为9×8=72个.

对于B中的三位数：百位数字有9种选法(可选1,2,…,9)；百位数字选定后，十位数字有8种选法(与十位数字不同，且不能是上面配对的数)；百位、十位数字均选定后，个位数字有6种选法(与百位、十位数字均不同，且均不能是上面配对的数).所以B中的三位数为9×8×6=432个.

(2)B中有五位数，比如12340.

因为在上面配成5对数的每对数中至多只能选一个作为B中数的数字，所以B中没有六位数.

(3)由(1)的结论知，B中的两位数、三位数共72+432=504个.同理可求得B中的四位数为9×8×6×4=1728个.

所以将B中的元素从小到大排列后，第1081个元素是四位数，且是四位数中从小到大的第1081-504=577个.

B中的四位数中，千位数字为1,2,3的各为8×6×4=192个，共192×3=576个，所以所求答案是将B中的元素从小到大排列后的最小四位数，即4012.