奇偶性在高考中的应用

陈建会

(河北省沧州市海兴县中学 061200)

一、结合奇偶性确定函数类型

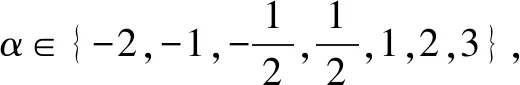
分析结合幂函数f(x)=xα为奇函数，且在(0，+∞)上递减，利用幂函数的基本性质确定参数α所满足的条件，进而结合题目中参数给出的已知值，求出相应α的值，得以正确确定幂函数的类型.

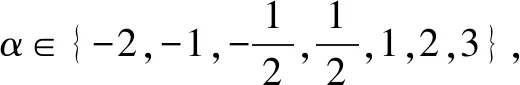
点评结合函数的奇偶性来确定函数的基本类型问题，关键是熟练掌握基本初等函数(指数函数、对数函数、幂函数等)的图象与性质，特别要注意的是对应的参数值与相应的性质之间的关系.

二、结合奇偶性确定参数值

例2(2019·全国Ⅱ卷理·14)已知f(x)是奇函数，且当x<0时，f(x)=-eax.若f(ln2)=8，则a=____.

分析结合函数的奇偶性确定f(-ln2)的值，并借助对应的函数的解析式建立相应的关系式，通过求解方程来确定相应的参数值.

解析由于f(x)是奇函数，则知f(-ln2)=-f(ln2)=-8.又当x<0时，f(x)=-eax，则有f(-ln2)=-e-aln2=-8，即-aln2=ln8，得a=-3，故填答案：-3.

点评结合函数的奇偶性来确定相应的参数值问题，关键是根据题条件，利用函数的奇偶性建立起相应的方程或对应的关系式，进而通过求解相应的方程或对应的关系式来达到确定参数值的目的.

三、结合奇偶性确定解析式

例3(2019·全国Ⅱ文·6)设f(x)为奇函数，且当x≥0时，f(x)=ex-1，则当x<0时，f(x)=( ).

A.e-x-1 B.e-x+1 C.-e-x-1 D.-e-x+1

分析结合函数的奇函数的定义得到f(-x)=-f(x)，通过已知解析式的转化加以确定当x<0时f(x)的解析式问题，进而得以正确判断.

解析由于f(x)是奇函数，所以当x<0时，-x>0，可得f(-x)=e-x-1=-f(x)，即f(x)=-e-x+1，故选择答案：D.

点评结合函数的奇偶性的定义以及不同条件下函数的解析式问题来确定相应的解析式问题，关键是正确掌握函数的奇偶性及其关系.解决此类问题特别要注意解析式中的符号，不要产生混淆.

四、结合奇偶性确定函数图象

分析结合函数的解析式以及函数奇偶性的定义判断已知函数的奇偶性问题，进而利用函数图象的对称性来排除相关的选项；再结合f(4)、f(6)的特殊取值情况继续排除相关的选项，从而得以正确判断.

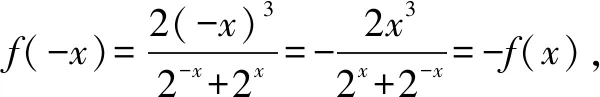
故选择答案：B.

点评结合函数的奇偶性来判断函数图象问题，往往通过函数的解析式并结合奇偶性的定义先确定其奇偶性，从而确定函数图象的对称性，再结合函数的其他基本性质、特殊点处的取值情况等来分析与判断.

五、结合奇偶性与单调性交汇

例5(2019·全国Ⅲ卷理·11；文·12)设f(x)是定义域为R的偶函数，且在(0，+∞)单调递减，则( ).

分析结合抽象函数的奇偶性加以转化，关键是通过奇偶性把对应的函数值转化为同一单调区间内，再借助复合函数的单调性性质，结合指数式与对数式的大小关系，进而达到判断代数式的大小关系.

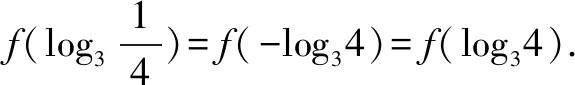
点评结合函数的奇偶性与单调性交汇来处理函数值的大小比较问题，经常借助指数函数、幂函数、对数函数等基本初等函数的图象与性质，以及对应的指数幂运算、对数运算等相关内容，融合“函数”与“图象”加以数形结合，是高考中比较热点的一类常见题型.

六、结合奇偶性与周期性交汇

例6(2018·全国Ⅱ文·12；理·11)已知f(x)是定义域为(-∞，+∞)的奇函数，满足f(1-x)=f(1+x).若f(1)=2，则f(1)+f(2)+f(3)+…+f(50)=( ).

A.-50 B.0 C.2 D.50

分析结合抽象函数的奇偶性与已知函数关系式，通过变形与转化来确定函数的周期性，再综合利用奇偶性与周期性的交汇知识，先确定一个周期内相应的函数值，再结合周期性特征来解决相应的函数值的求解问题.

解析由于f(x)是定义域为(-∞，+∞)的奇函数，且满足f(1-x)=f(1+x)，可得f(x+1)=f(1-x)=-f(x-1)，则有f(x+4)=-f(x+2)=f(x)，则知函数f(x)的周期为T=4.由f(x+1)=-f(x-1)，及f(1)=2，可得f(3)=-f(1)=-2.又f(2)=f(-2)=-f(2)，则有f(2)=0，可得f(4)=-f(2)=0.那么f(1)+f(2)+f(3)+f(4)=0，所以f(1)+f(2)+f(3)+…+f(50)=12×0+f(49)+f(50)=f(1)+f(2)=2，故选择答案：C.

点评结合函数的奇偶性与周期性交汇知识来综合考查函数的求值问题，破解问题的关键是巧妙综合利用奇偶性及周期性进行合理转化与变换，进而将所求解的函数值的自变量转化到已知解析式的函数定义域内来分析与求解.

历年高考都对函数内容进行重点考查，往往都离不开函数的奇偶性，此类考题经常幂函数、指数函数和对数函数等为背景，综合基本初等函数的图象与性质以及相关的运算，有时单独考查奇数性问题，有时综合考查奇偶性与其他相关性质的交汇问题，这一类试题出现在小题(选择题或填空题)中，难度属于较易型或中等型.