基于LSTM-SVM的卷对卷系统预测性维护模型

黄冠泽

（广东工业大学，广州 510006）

0 引言

随着柔性材料加工技术的快速发展，柔性薄膜材料的制备工艺也不断得到完善。新型柔性薄膜材料制品，如柔性电路板、太阳能电池薄膜等在各个行业的使用日益增多。柔性材料卷对卷设备（Roll to Roll，R2R）作为薄膜材料的主要生产设备之一，被广泛应用到柔性电路板（FPC）、有机发光二极管（OLED）、太阳能电池薄膜、干粘合剂等柔性薄膜材料的制备生产当中[1-3]。卷对卷设备加工过程具有高速、高精度、持续生产的特点。当其核心零部件发生性能衰退，加工精度将大幅度下降，引起柔性薄膜产品的变形，使得良品率降低，造成经济损失。非常有必要对卷对卷设备进行预测性维护。

近年来，有学者进行了LSTM（Long Short-Term Memory）在预测性维护领域的应用研究[4-7]，取得了一定进展，证明了LSTM 网络在预测性维护领域应用的可行性。但是LSTM网络的预测结果仍存在误差叠加及预测结果滞后[8]、学习速率低[9]等问题。Funa[10]中提到，建立RUL 预测模型时，传统的LSTM模型不能合理利用在线数据和非生命周期数据。

金樑[11]中提出一种SVM 算法加权融合LSTM 算法的模型，在短期电力负荷预测实验中得到不错的结果，预测误差小且速度快，表明SVM 对于LSTM 神经网络具有降低预测滞后率的效果。因此，本文提出了LSTM-SVM 算法融合预测模型，将完整且经过训练的LSTM 模型的softmax 输出层更换为SVM分类器，再进行SVM分类器的训练，最后得到LSTM-SVM算法融合模型。又由于自身算法的抗拟合特性，SVM 常被用于解决神经网络过拟合的问题[7]，提升算法融合网络的抗过拟合特性。SVM 在处理低维数据分类问题时，速度更快，精度更高，作为网络的输出层时，能很好地对LSTM网络所提取的特征数据进行分类。最后经过实验证明，本文提出的LSTM-SVM 算法融合预测模型得到的健康状态层级多，预测精度高，能很好地进行卷对卷设备预测性维护。

1 LSTM-SVM神经网络模型框架

本文提出了一种基于LSTM 神经网络和SVM 神经网络的性能衰退预测模型——LSTM-SVM模型。图1所示为性能衰退预测模型的结构。该模型由两部分组成，第一部分是深度递归循环神经网络，采用LSTM神经网络从原始输入向量中提取数据特征；第二部分是用来进行特征分类的SVM神经网络输出层。LSTM神经网络最后一层的隐含层表示作为设备健康状态概括的表示输入到SVM神经网络层中。

该融合模型的训练方式为：首先训练LSTM模型，将轴承振动加速度数据经过标准化后输入到网络中，然后获得经过调整的神经元参数，输出隐含层信息。将隐含层信息输入到SVM分类器中，进行特征数据的分类，从而获得健康状态。

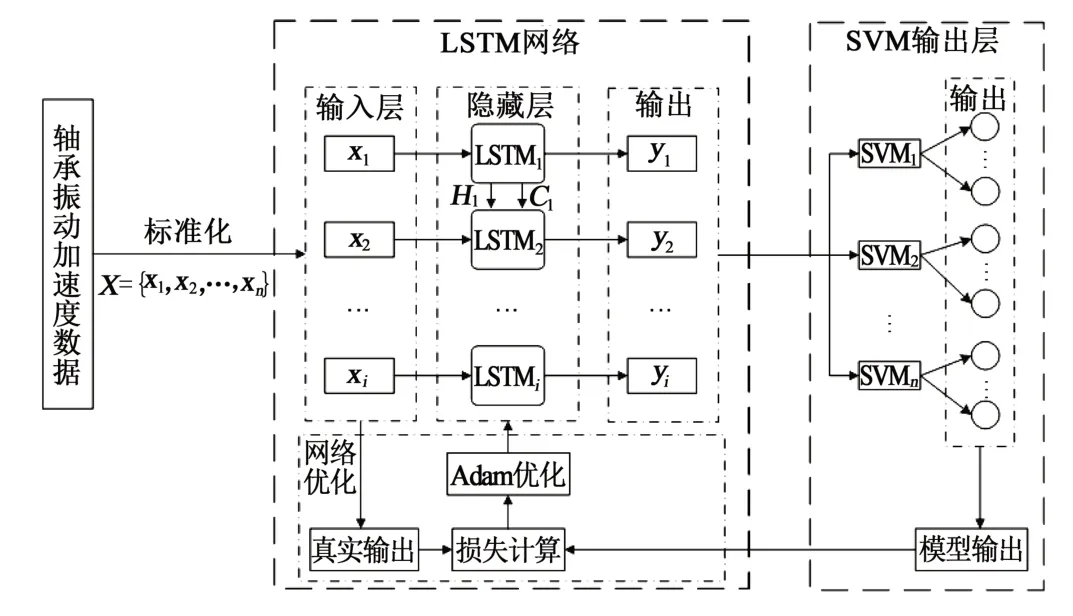
图1 LSTM-SVM性能衰退预测模型

2 基于LSTM-SVM 的卷对卷设备性能衰退预测模型建模

2.1 LSTM（Long Short-Term Memory）

LSTM 是RNN（Recurrent Neural Network）的改进模型之一，即LSTM 也是递归神经网络，具有递归神经网络的特性，常常被用于处理时间序列数据。当LSTM处理分类问题时，其输出层一般为softmax 逻辑回归网络[12]。该模型的基本单元是记忆模块，包含记忆单元和3个控制记忆单元状态的门结构，分别是遗忘门、输入门和输出门。遗忘门决定从记忆状态信息中遗忘相关度低的历史信息，而输入门决定记忆单元状态对输入数据对的敏感程度，输出门决定输出该时刻的信息。图2 所示为t时刻的LSTM 记忆模块状态。ft、it、ot分别为t时刻遗忘门的状态值、输入门的输入和输出门的输出；ht-1为记忆模块输入的隐含信息；ht为记忆模块输出的隐含信息；xt为t时刻的输入向量；gt和kt为计算过程为了方便计算而设定的中间量；Ct-1为t-1时刻的记忆单元状态；Ct为t时刻的记忆单元状态；C~t为记忆单元的中间状态。

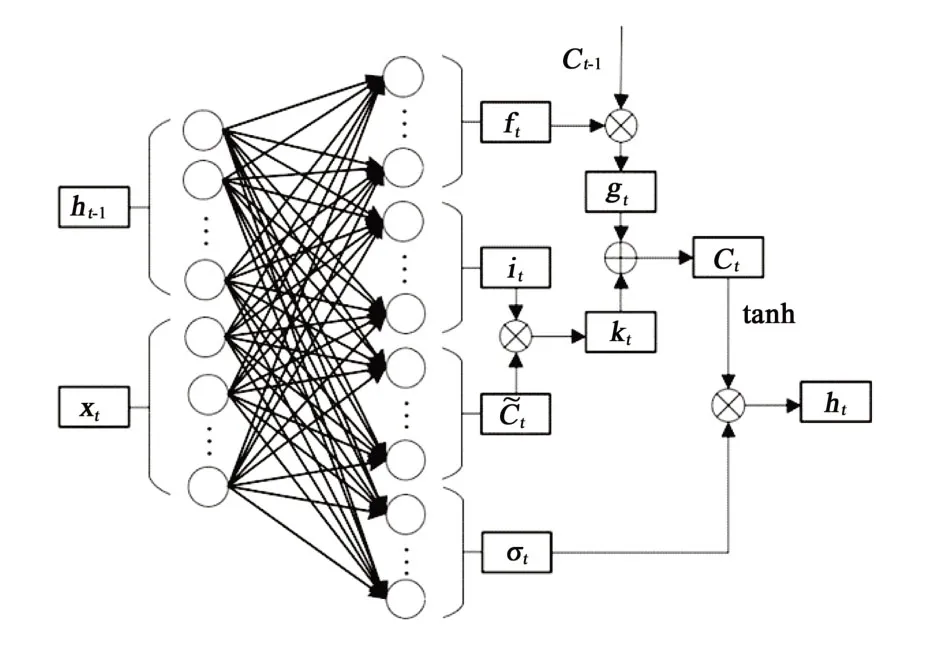
图2 LSTM记忆模块

LSTM记忆单元状态更新和输出信息的过程如下。首先，通过遗忘门删除相关度低的历史信息：

然后，输入门根据输入信息和历史信息来更新序列信息：

设gt=ft×Ct-1，kt=it×C~t，则有Ct=gt+kt。最后，输出t时刻的信息为：

式中：U为隐含状态h的权重矩阵；W为输入状态x的权重矩阵；Uf、Ui、UC、UO、Wf、Wi、WC、Wo分别为对应门的权重矩阵；bf、bi、bC、bO分别为对应门的偏置向量；σ为sigmoid激活函数；tanh为双曲正切激活函数。

LSTM 网络需要设置的超参数Input time step、Input Dimension、Output Units、Batch Size、Epoch、Optimizer、Learning Rate、Decay、Dropout rate 等。Input time step 为时间步，即每次输入数据的长度；Input Dimension为输入维度，即输入数据的维度；Output Units 为输出类，即输出层输出类别的数目；Batch Size 为单次训练样本数；Epoch 为模型训练次数；Optimizer为优化算法，即将模型梯度下降的算法；Learning Rate为模型的学习率，可直观表示模型的学习性能；Decay为衰减率，是正则项的一个系数，控制权值衰减的速率，用于防止过拟合；Dropout rate 为丢失率，用于在模型训练途中，去掉冗余的神经元，留下贡献更高的神经元，以提高模型性能。

2.2 支持向量机

支持向量机（support vector machines, SVM）是一种用于解决二分类问题的模型，通过求解数据簇在特征空间上的最大间隔来进行线性分类。添加核函数后，SVM 转变为非线性分类器。间隔最大化是SVM的学习策略，具体为求解凸二次规划。其基本过程是求解划分训练数据簇并且几何间隔最大的超平面，用w·x+b=0 表示。在平面上，w 可视为直线的斜率，b为直线的截距。

对于给定的数据集T={(x1,y1),(x2,y2),…,(xN,yN)}和分离超平面w·x+b=0，超平面关于样本点的几何间隔定义如下式所示：

具体地，K(x,z)是一个函数，或正定核，存在一个映射φ(x)，对任意输入空间中的x，z，都满足下式条件：

K(x,z)=φ(x)·φ(z) （8）

用核函数K( x, z )代替内积，求解得到非线性支持向量机。参数α*为拉格朗日乘子，且α*>0。

非线性支持向量机的学习算法如下。

输入：训练数据集T={( x1, y1), ( x2, y2), …, ( xN, yN)}。其中，xi∈ℝn，yi∈{+1,-1}，i=1,2,…N。

输出：分离超平面和分类决策函数。选取适当的核函数K(x,z)和惩罚参数C>0，构造并求解凸二次规划问题。其中，0 ≤αi≤C，i=1,2,…N。

选择α*的一个分量满足条件

得到最优解分类决策函数如下式所示：

高斯核函数是SVM处理非线性问题的常用核函数，如下式所示：

将上式代入分类决策函数，得到下式：

根据以上理论不难看出，SVM 算法在处理低维数据分类问题时，由于其算法复杂程度低，可以同时进行大量数据的计算，计算效率极高，且精度较高。结合SVM自身的抗拟合特性，其常被用于解决神经网络过拟合的问题，提升了算法融合网络的抗过拟合特性。作为网络的输出层时，能很好地对LSTM网络所提取的特征数据进行分类。

构建SVM分类器，需要设置惩罚参数C和几何间隔γ，C用来约束α*i的范围，防止模型出现过拟合和欠拟合的现象。为了简化计算，可将γ设置为1。

2.3 LSTM-SVM神经网络模型参数

根据上述原理，构建LSTM-SVM 神经网络模型，表1 所示为LSTM网络的参数设置情况。时间步与输入数据的长度相同，设置为1000。由于数据的维度对本实验的影响不大，不对数据进行压缩，故输入维度为1维。输出类与数据标记类相同，即为健康状态的个数，定为100类。由于训练模型的计算机显卡并行计算的特性，单次训练样本数需要定为2 的幂次方，即2、4、8、16、32、64 等。根据实验数据量，取32 为单次训练样本数，有助于模型的训练。将模型训练次数设置为15 次，观察模型损失值的变化。RMSProp 优化算法是AdaGrad算法的一种改进，加了一个衰减系数来控制历史信息的获取多少，所以在优化用于处理时序问题的模型时，更具有优势。学习率根据经验默认为0.001；衰减率定为0.9，防止因样本数量小而导致过拟合；丢失率定为0.5，即在每次训练过程中，将模型中一半的神经元清零，以提高贡献度高的神经元的权重。

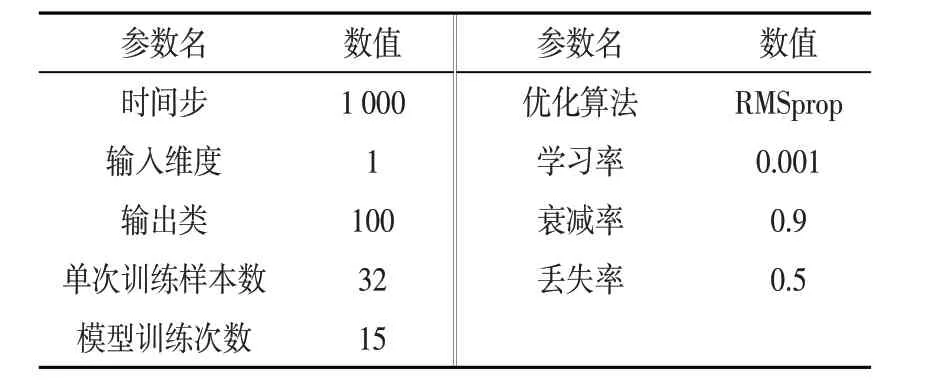
表1 LSTM网络参数设置

表2 所示为SVM 层的参数设置情况。惩罚参数C用来约束的范围，防止模型出现过拟合和欠拟合的现象，取中值，设为0.5。在低维问题中，几何间隔的值对SVM分类器的性能影响不大，为了简化计算，可将γ设置为1。以此，训练SVM分类器100 个，作为LSTM-SVM 的输出层，划分卷对卷设备的健康状态。

表2 SVM层参数设置

3 LSTM-SVM性能衰退预测模型试验研究

3.1 搭建实验平台

图3 为搭建LSTM-SVM 性能衰退预测模型实验平台，用于验证LSTM-SVM 性能衰退预测模型的性能。该平台为安捷利FPC 产线的收卷装置，是FPC 产线制备柔性电路板的关键装备之一。在其辊轴上安装振动加速度传感器，将传感器连接采集卡以采集数据。在完整的寿命周期中，采集轴承的振动信号。实验条件参数如表3所示。数据的采集频率为20 kHz，每10 min采集1次，每次采集20480个数据点。

图3 LSTM-SVM 性能衰退预测模型实验平台

表3 实验条件参数

为了训练网络模型，需要在计算机上搭建虚拟环境，其配置如表4所示。采用了Pycharm作为网络模型程序运行的编译器，并在其环境中调用常见的AI 模型框架Tensorflow 作为LSTM-SVM模型的框架。

表4 虚拟环境搭建配置

3.2 实验测试及结果分析

LSTM-SVM 性能衰退预测模型针对卷对卷设备辊轴出现的性能衰退问题，对其进行性能衰退预测，为设备维护提供决策依据。卷对卷设备高速运行，重要组成部分即将失效，将导致设备整体报废，造成严重损失。现在对其进行性能衰退预测实验。

实验分为两部分。首先，使用训练集训练神经网络模型。然后，使用验证集验证已训练模型的性能。对数据情况进行分析。

R2R 设备性能衰退有4 个状态，分别为性能良好状态、前期衰退状态、中期衰退、辊轴失效等。可以用相应的原始轴承信号表示，在不同性能状况下轴承振动信号如图4所示。

从良好状态的振动信号数据中随机取10组数据，标记为最高健康状态（即满分100，分值为0～100，0 为衰退失效），再从前期衰退状态到辊轴失效状态间的振动信号数据中，按比例取100 组数据作为训练集，依次标记为99、98、97、…、1、0分。同理，另取110 组数据作为验证集。每组数据含数据点1000 个，采样时间为0.05 s。对应网络模型结构为1000-100-100-100，即输入层含1000 个神经元，输出层含100个SVM分类器，即输出100类。另外，两个隐含层的含100个神经元。

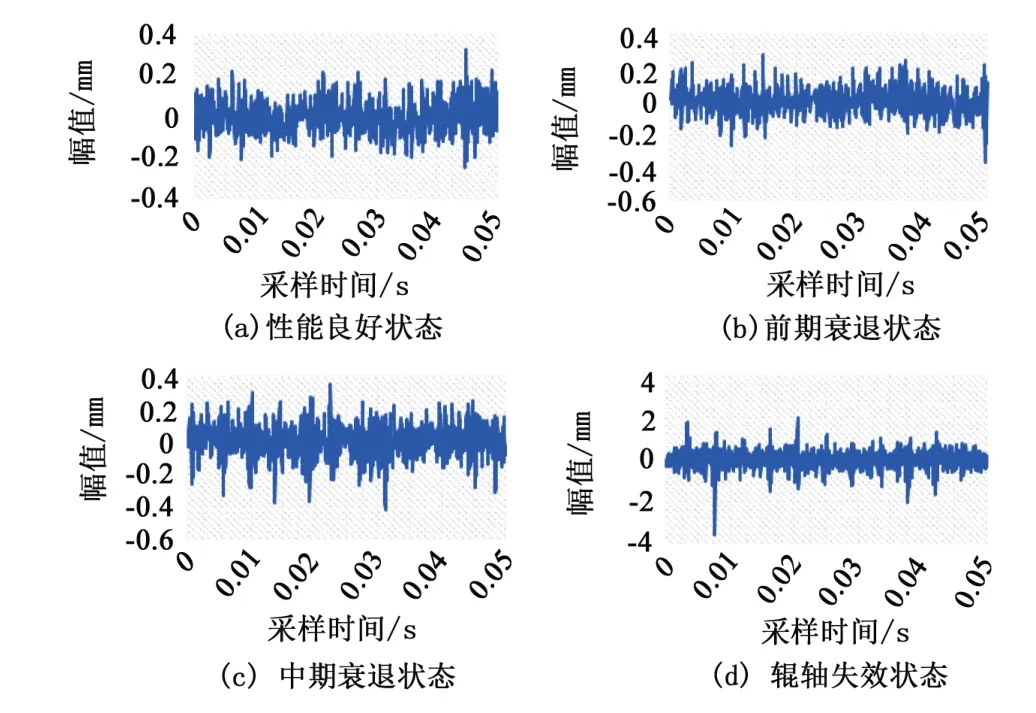
图4 原始轴承振动信号

为了评估LSTM-SVM 模型在性能衰退预测上的性能，采用损失值和准确度来量化LSTM-SVM 模型的性能。损失值是预测值和真实值之间概率分布差异的量化，损失值越小则表明预测值越接近真实值，损失值的计算公式下式所示。

式中：y为真实值；y^为预测值；w为模型参数。

准确度为模型输出结果的总结，能直观表现模型的预测性能。准确度越高表明模型性能越好。

训练模型得到其损失函数曲线如图5 所示。可以看出，当LSTM-SVM 模型训练第7 次时，训练集的损失值基本收敛到0.47，继续训练模型得到的收益较低。而验证集在模型训练第8次时，这是由训练集和验证集的数据差异性导致的，所以验证集的损失值收敛在0.38，优于训练集的结果。

图5 LSTM-SVM模型的损失函数曲线

图6 LSTM-SVM模型的预测准确度曲线

模型训练过程中准确度曲线如图6 所示。实验结果最终得到，训练集的准确度为0.620，验证集的准确度为0.535。因为模型采用训练集来训练，对训练集的拟合程度更高，故准确度比验证集高。

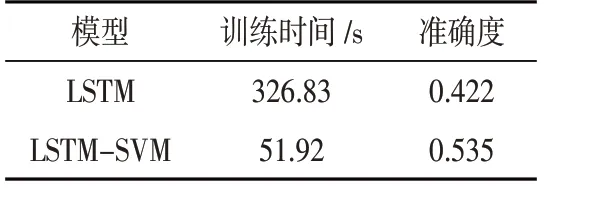
表5 模型训练效果对比

为了验证LSTM-SVM模型的预测性能，本研究建立了LSTM-SVM模型与LSTM 模型的对比实验。LSTM 模型使用相同的训练集和验证集。经过验证，两种模型的效果对比如表5所示。

通过两种预测模型的对比实验，可以发现LSTM-SVM 的训练速度比LSTM模型快很多，而且精度也有所提升。

4 结束语

本文针对柔性材料卷对卷设备的性能衰退问题，提出了一种LSTM-SVM 性能衰退模型。通过实验发现LSTM-SVM 模型有效预测了卷对卷设备的性能衰退情况，成功划分了设备的健康状态且模型拟合情况良好，表明该模型在卷对卷设备性能衰退预测方面具有可行性。最后进行了对比实验，发现LSTM-SVM的训练速度比LSTM模型快很多，而且预测精度也有所提升。该结果表明SVM 能很好地对LSTM 网络所提取的特征数据进行分类。这是因为模型很好地融合了SVM在处理低维数据分类问题时的优越性。而更快的学习速率意味着，当算力一定时，用于训练的数据规模可以更大，这对于工业大数据而言十分具有应用前景。综上，本文提出的LSTM-SVM 性能衰退预测模型得到的健康状态层级多、训练时间短、预测精度高，能很好地进行卷对卷设备预测性维护，为后续的柔性材料卷对卷加工决策系统提供重要决策依据。