近57年金沙江流域气温变化特征及未来趋势预估
史雯雨, 杨胜勇, 李增永, 高剑飞, 潘 露
(四川水利职业技术学院, 成都 611231)
随着全球气候变化问题日益突出,气温作为气候的基本要素,逐步受到各国政府及学者的研究关注[1]。IPCC第五次研究报告指出,近百年全球气温上升已高达0.85~0.89℃,气温呈现显著的升高趋势[2]。近年来,我国气温变化特征引起了不少研究人员的关注[3-6],研究发现我国气温近60 a呈现明显的上升趋势,全国平均气温变化递增率为0.25℃/10 a,且区域性和季节性差异显著。金沙江流域作为长江源头河流,气候变化会使水资源供给条件发生变化,进而影响生态环境和社会经济的发展,而气温作为最基本的气候要素,对生态环境的变迁起着决定性作用[7]。目前,针对金沙江流域的气温要素已经开展了很多研究工作,并取得了一些研究成果。陈媛等[8]对金沙江流域及各个站点的年气温和年降水进行了趋势、周期和突变分析。施晨晓等[9]分析了金沙江流域30个站点年及四季的气温和降水时间和空间变化趋势。现有文献大多以金沙江流域平均气温作为研究对象进行分析和研究,研究年限较短,并且未对未来的变化趋势进行预测分析;平均气温并不能涵盖气温普遍范围,一般来说,平均最高气温、平均最低气温和平均气温可基本涵盖气温的普遍范围,且三者的变化特征却不尽一致。因此,仅仅分析平均气温的变化特征不足以涵盖气温普遍范围内的特征,研究这3类气温更具有意义和价值[10]。本文主要对金沙江流域的平均最低气温、平均最高气温和平均气温进行趋势、周期分析,为金沙江流域的开发利用提供科学的气候变化背景;同时对金沙江流域未来气候变化进行预测,对防灾减灾及生态建设具有重要的意义。
1 资料来源和研究方法
1.1 资料来源
为了保证资料的完整性,本文选取金沙江流域分布相对均匀的39个气象站点,金沙江流域气象站点分布见图1。选用国家气象科学数据共享服务网平台提供的各站点1960—2016年的逐日平均气温、逐日平均最高气温和逐日平均最低气温数据作为基本资料。国家气象中心对各气象站的气温数据已进行了质量控制,在此基础上对数据进行了时间一致性检验和极值检验,利用RClimDex软件进行了进一步的质量控制;部分站点存在数据缺测的现象,但缺测时间所占比例很小,本文采用相邻站点线性回归方法对个别站点的缺测资料进行插补处理,经过处理修正后的39个气象站的资料具有比较好的连续性,保证气温序列的完整性。

图1 金沙江流域位置及气象站点分布
1.2 研究方法
采用累计距平法、Mann-Kendall检验法、Morlet小波分析法和Hurst指数法分别对金沙江流域年及四季的平均气温、平均最高气温、平均最低气温变化特征及未来趋势进行分析;其中四季按照春季(3—5月),夏季(6—8月),秋季(9—11月),冬季(12月—次年2月)进行划分。
(1) Mann-Kendall。Mann-Kendall检验(以下称M-K检验)是由世界气象组织推荐并已经被广泛应用到降水、气温、径流等气象和水文研究的一种非参数检验方法,其优点是不需要样本系列遵从一定的分布,也不受少数异常值的干扰,适用于非正态分布的时间序列。
对于给定置信水平α,若M-K统计量|Z|
(2) 小波分析。小波分析是一种具有时—频多分辨率功能的方法,它能清晰地揭示出隐藏在时间序列中的多种变化周期,对处理非平稳水文气象序列具有独特的优点,能从时域和频域上精确解释信号细微的时频变化特征[14]。
由于采用连续Morlet小波作为基函数进行小波变换,能够很好地对气温序列连续进行时频局部化分析。因此,本文选用Morlet小波进行分析研究,利用小波变换得到一个时间尺度函数,并且通过对小波方差的研究进行分析检验,从而确定主周期。小波方差反映了能量随时间尺度的分布情况,其峰值即为时间序列变化的主周期[15-16]。
(3) Hurst指数法。Hurst指数法也称为重标极差分析法,是由英国水文学家Hurst提出,Hurst指数法常应用于分析时间序列的分形特征和长期记忆过程,现被广泛应用于判断时间序列变化趋势的持续性或反持续性的强度,一般采用R/S分析法来计算[17-18]。
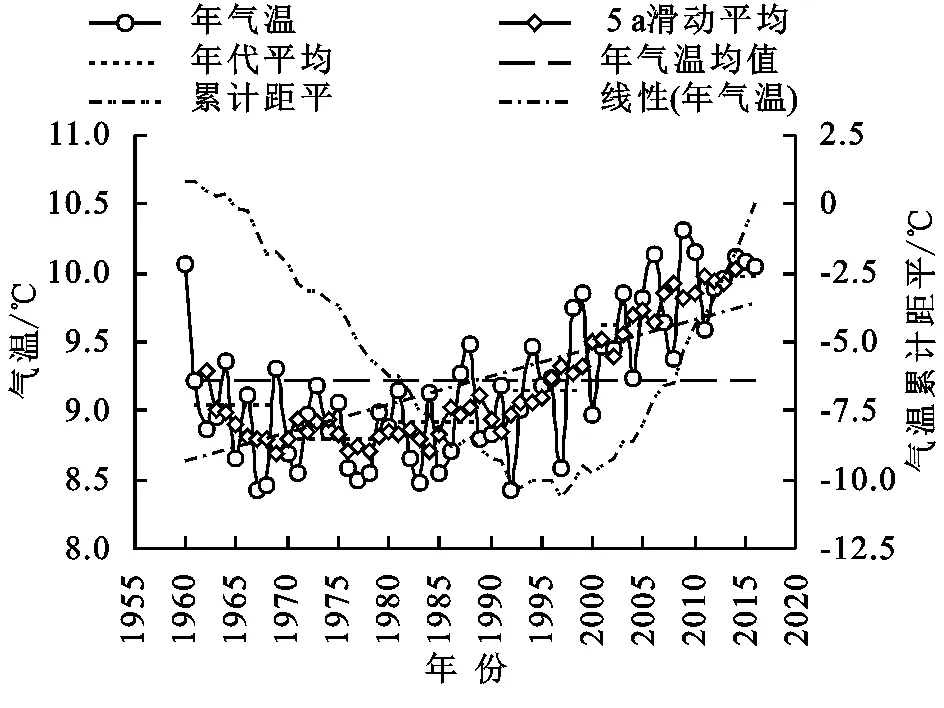
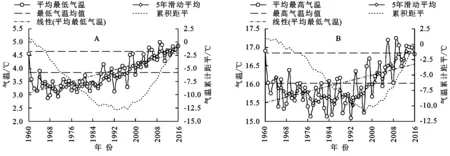
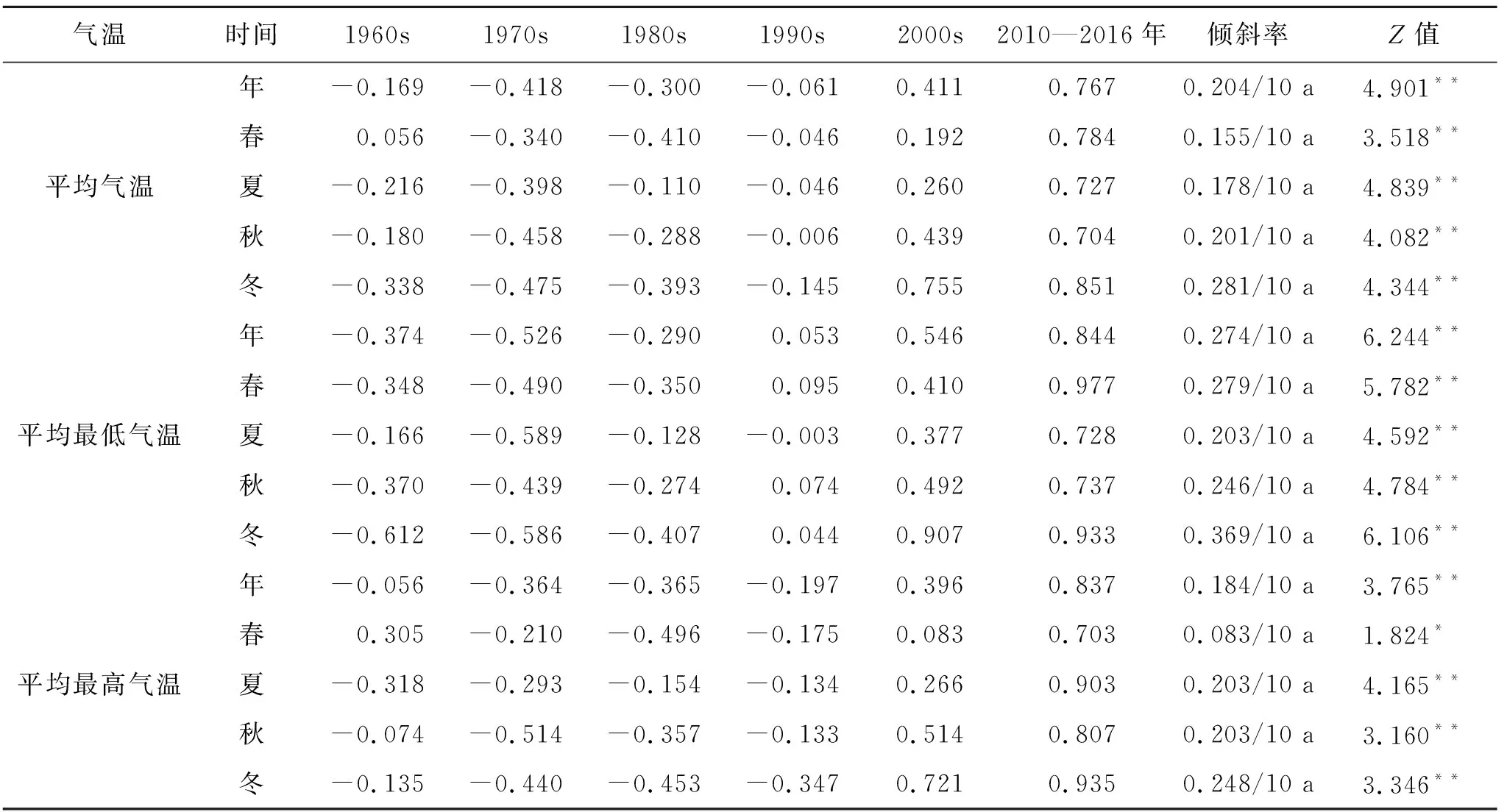
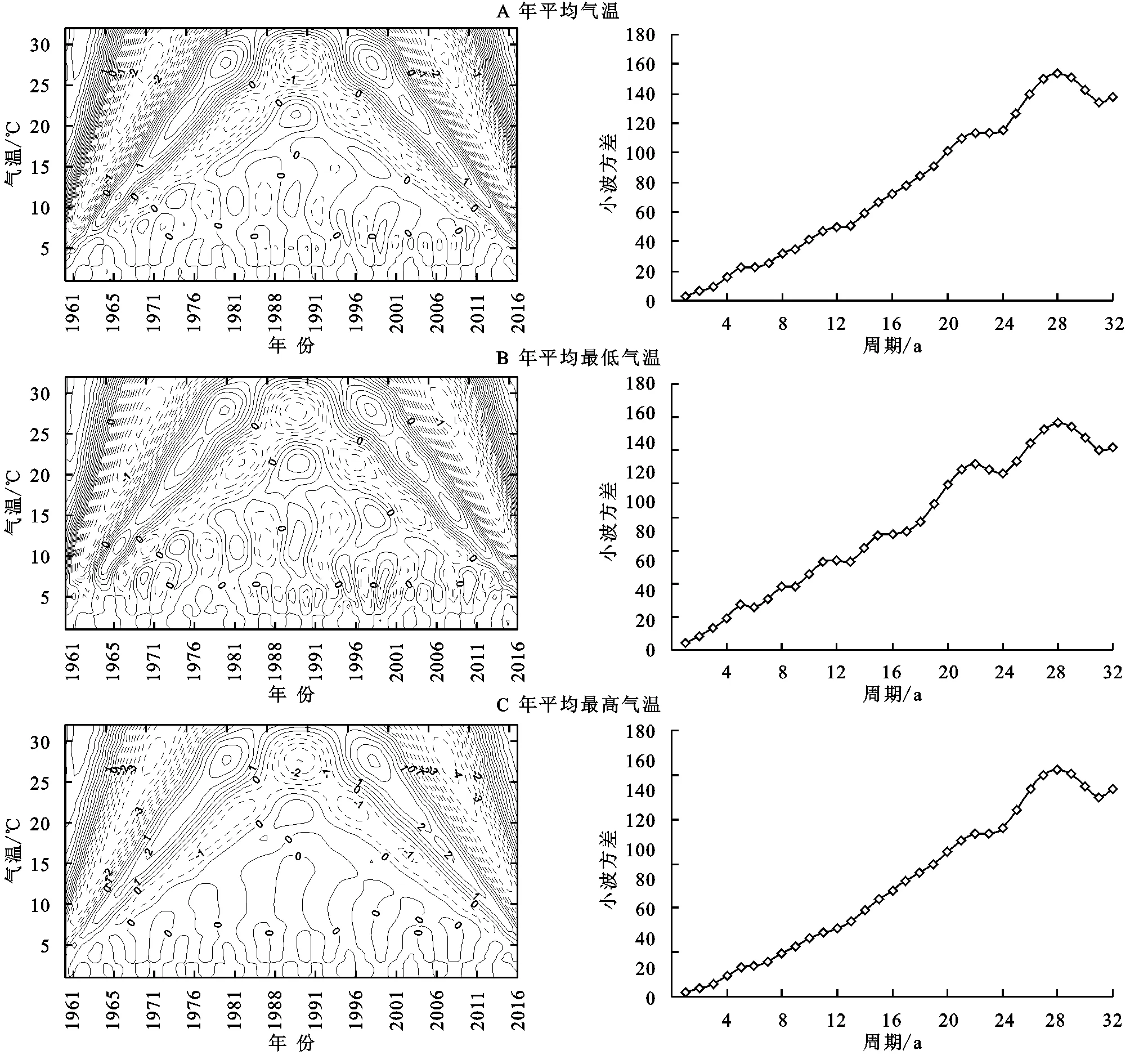
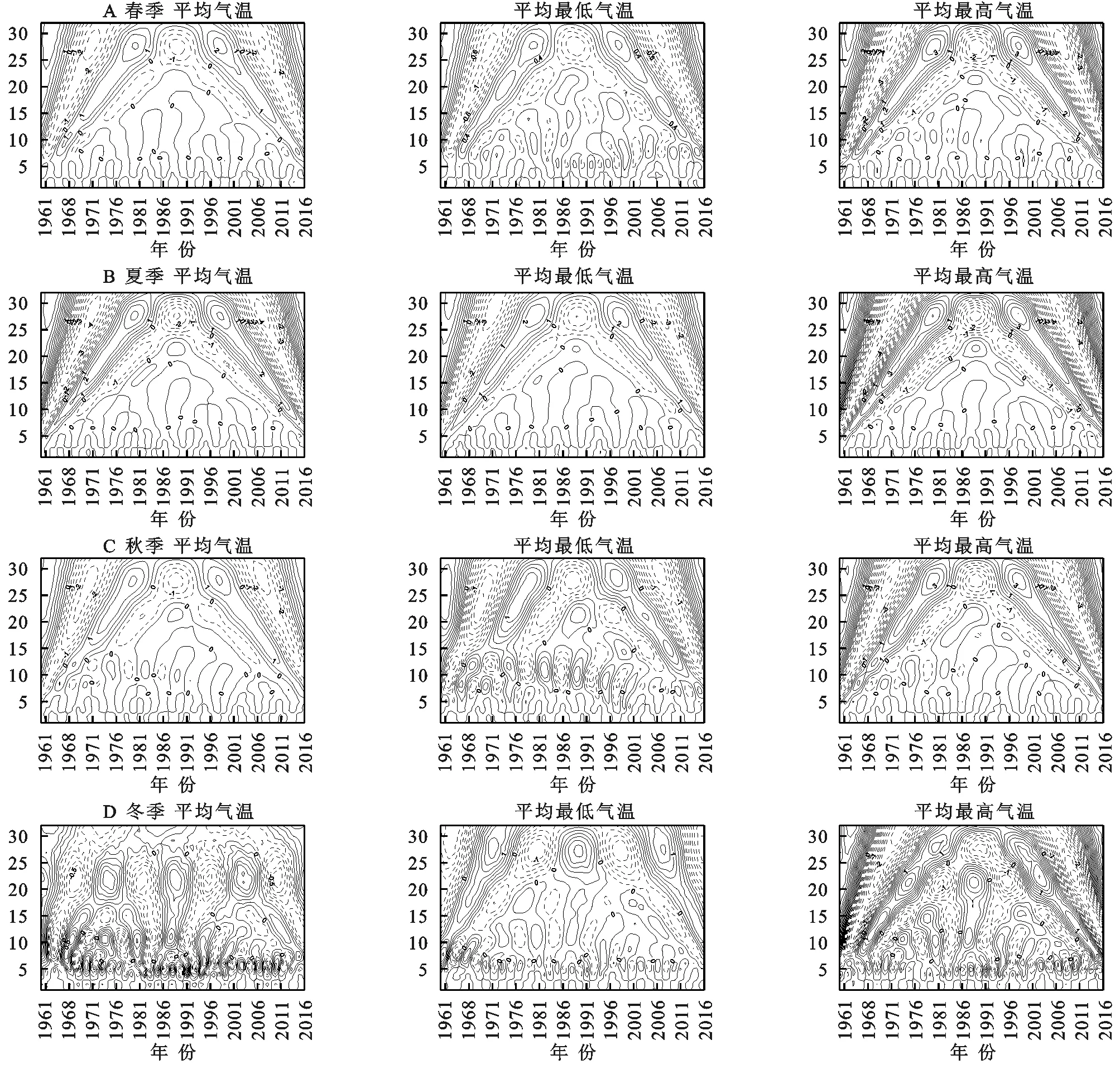
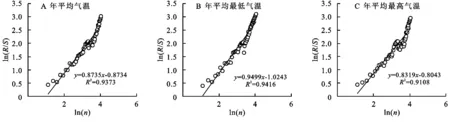
不同Hurst指数的H值意味着不同的趋势变化,当0 表1 Hurst指数分级 金沙江流域1960—2016年的多年平均气温为9.21℃,由金沙江流域年平均气温年际变化趋势可知,金沙金流域年平均气温总体呈现上升趋势,其上升倾斜率为0.20℃/10 a,且通过置信度为99%的Mann-Kendall显著性检验,说明金沙江流域近57 a来年平均气温呈现显著的上升趋势;由图2可知,金沙江流域年平均气温在1991年前后呈现两种截然不同的变化趋势,1991年之前年平均气温基本呈平稳的波动变化,1992年以后年气温呈明显的波动上升趋势;由累积距平可知,1960—1997年累积距平曲线呈下降趋势,在1997年达到最低值-10.67℃,1997年以后累积距平曲线呈现显著的上升趋势。 图2 金沙江流域年平均气温年际变化趋势 图3为金沙江流域年平均最低气温和年平均最高气温年际变化趋势过程线,由图可知,金沙江流域1960—2016年的年平均最低气温和年平均最高气温平均值值分别为3.84℃和16.02℃;金沙金流域年平均最低气温和平均最高气温总体呈现上升趋势,其上升倾斜率分别为0.27℃/10 a和0.18℃/10 a,均通过置信度为99%的Mann-Kendall显著性检验,说明金沙江流域近57 a来年平均最低气温和年平均最高气温均呈现显著的上升趋势,且年平均最低气温上升趋势高于年平均最高气温的上升趋势;由累积距平可知,年平均最低气温累积距平曲线在1960—1993年呈下降趋势,在1993年达到最低值(-12.773℃),而后呈现平缓波动变化,并在1997年达到次低值(-12.769℃),1997年以后累积距平曲线呈现显著的上升趋势,年平均最高气温累计曲线变化趋势基本与年平均气温一致。 图3 金沙江流域年平均最低气温(A)和年平均最高气温(B)年际变化趋势 由气温年代距平值可知:(1) 金沙江流域年平均气温、平均最低气温和平均最高气温均呈现上升趋势,并均通过99%显著性检验,其中平均最低气温增幅最大,说明平均最低气温对气温上升的贡献率最大。(2) 年及四季的平均气温距平值最高均出现在2010—2016年,表明该时期是自1960年以来最暖的一个时期;年平均气温距平在1990s以前均为负值,1970s温度最低是异常偏冷期,进入21世纪距平值为正且呈现逐渐增加趋势,其中2000s较1990s增温幅度最大为0.472℃。(3) 年及四季的平均最低气温变化类似于平均气温变化,冬季平均最低气温距平值最低出现在1960s,年及其余三季平均最低气温距平值最低均出现在1970s;年及四季平均最低气温距平最大值出现在2010—2016年;春季最低气温2010—2016年较2000s增幅最大,年及其余三季均是2000s较1990s增温幅度最大。(4) 年及四季的平均最高气温变化稍有所差异,最高气温距平最大值均出现在2010—2016年;年、春季和冬季平均最高气温距平最低值出现在1980s,夏季和秋季平均最高气温距平最低值分别出现在1960s和1970s;年、秋季和冬季平均最高气温2000s较1990s增温幅度最大,其中冬季最高气温增幅高达1.068℃,春季和夏季平均最高气温2010—2016年较2000s增幅最大(表2)。 表2 金沙江流域年及四季气温距平的年代际变化及M-K统计值 2.2.1 年气温周期分析 金沙江流域年平均气温、年平均最低气温和年平均最高气温小波系数等值线图见图4,图中实线表示小波系数为正值,气温偏暖;虚线表示为负值,气温偏冷;等值线上的小波系数的大小表示信号的强弱,与周期显著性的强弱成正比,若小波系数等于零,则表示为突变点。 图4 金沙江流域年气温小波系数实部等值线图及小波方差图 由图可知,金沙江流域年平均气温、年平均最低气温和年平均最高气温序列的小波变换实部及对应的模值能明显的反映出周期震荡及时间尺度特征。金沙江流域年平均气温、年平均最低气温在26~30 a左右的震荡周期最为明显,其次是4~7 a,9~15 a,20~24 a,其中,4~7 a在20世纪60年代中期至70年代中期和1981—2016年这两个时域表现显著;9~15 a在20世纪70年代至90年代末有较强的信号;20~24 a在1960—2005年的时间段有较强的信号;26~30 a时间尺度上的震荡是全时域的,呈现出高—低—高—低—高—低3个较为完整的震荡周期,且目前正处于第4次气温偏高阶段,说明在未来几年内流域气温很可能仍处于气温偏高期。金沙江流域年平均最高气温在26~30 a和20~24 a左右的震荡周期较为明显,其中28 a左右时间尺度能量最强,周期最为显著,为主周期。 小波方差能反映出信号波动的能量随时间尺度的分布,由小波方差图可知,金沙江流域年平均气温、年平均最低气温及年平均最高气温主要存在2个波峰,分别对应的是21 a和28 a。其中28 a左右的时间尺度能量震荡最强烈,对小波方差贡献最大,周期最显著,为主周期,21 a时间尺度能量震荡相对较弱,为次主周期。 2.2.2 四季气温周期分析 金沙江流域四季平均气温、平均最低气温和平均最高气温的周期变化呈现一定的差异性。(1) 近57 a以来金沙江流域春季平均气温、平均最低气温和平均最高气温均存在28 a和22 a左右的震荡周期,其中28 a左右的周期能量最强,周期最显著,且周期表现非常稳定,此外春平均最低气温还存在5 a左右的震荡周期;(2) 夏季平均气温、平均最低气温和平均最高气温存在28 a左右的震荡周期,且周期表现非常稳定;(3) 秋季平均气温和平均最高气温震荡周期基本一致,均存在28 a,22 a左右的震荡周期,经历了高—低—高—低—高—低3个震荡周期,但秋季平均最低气温存在28 a,22 a和12 a左右的震荡周期,其中28 a左右的周期能量最强,周期表现非常稳定;(4) 冬季平均气温存在5 a,11 a和22 a左右的震荡周期,其中22 a左右的周期能量最强,周期最为显著,且周期表现非常稳定;冬季平均最低气温在6 a,18 a和28 a左右的震荡周期,其中28 a左右的周期能量最强,为主周期;冬季平均最高气温在5 a,11 a,22 a和28 a左右的震荡周期,其中22 a左右的周期能量最强,为主周期。 通过对金沙江流域年和四季平均气温序列Hurst指数进行分析(图5—6,表3),金沙江流域年及四季的平均气温、平均最高气温、平均最低气温序列的Hurst指数均大于0.5,表明各气温序列具有长程相关性,即未来一段时间范围内,金沙江流域年及四季的平均气温、平均最高气温、平均最低气温变化情况与过去近57 a的上升趋势相同,气温将呈持续上升的趋势。 表3 金沙江流域气温Hurst指数及强度等级 图5 金沙江流域四季气温小波系数实部等值线 图6 金沙江流域年气温序列Hurst指数 金沙江流域年平均气温、年平均最高气温和年平均最低气温Hurst指数均大于0.8,Hurst指数等级为5级,持续性强度表现为很强,其中年平均最低气温持续性强度表现最为显著。 就四季而言,四季的年平均气温Hurst指数等级位于3~5级,夏季和秋季持续性强度表现为很强,春季表现为较强;四季的年平均最低气温Hurst指数等级均位于5级,持续性强度表现为很强,表明四季平均最低气温未来均将呈现很强的上升态势;四季的年平均最高气温Hurst指数等级位于3~5级,秋季持续性强度表现为很强,冬季表现为较强。综上,金沙江流域气温总体表现出明显的Hurst现象,未来保持当前继续上升趋势的概率比较大。 (1) 金沙江流域年平均气温、平均最低气温和平均最高气温均呈现波动上升的趋势,增长率分别为0.20℃/10 a,0.27℃/10 a和0.18℃/10 a,并均通过99%显著性检验,其中平均最低气温增幅最大,说明平均最低气温对气温上升的贡献率最大。 (2) 从四季来看,四季的平均气温、平均最低气温和平均最高气温也均呈现波动上升的趋势,并均通过90%显著性检验,其中夏季平均气温和平均最高气温对平均气温和平均最高气温贡献率最大,冬季平均最低气温对平均最低气温贡献率最大;从年代际变化来看,年和季节的平均气温、平均最低气温和平均最高气温自20世纪90年代开始增温,且呈现加速上升趋势,年代际距平最大值出现在2010—2016时间段。 (3) 金沙江流域年气温存在3个不同时间尺度的主周期,分别是6 a,21 a和28 a。其中28 a左右的时间尺度周期最显著,为主周期。春季、夏季平均气温存在28 a,22 a和6 a左右的震荡周期,秋季平均气温存在28 a,22 a和13 a左右的震荡周期,均以28 a的震荡周期为主周期;冬季平均气温在22 a和11 a,6 a左右的震荡周期,其中22 a左右的周期能量最强,周期最显著。 (4) 金沙江流域气温总体表现出明显的Hurst现象,未来保持当前继续上升趋势的概率比较大。年平均气温、年平均最高气温和年平均最低气温Hurst指数均大于0.8,Hurst指数等级为5级,持续性强度表现为很强,其中年平均最低气温持续性强度表现最为显著;四季的气温序列Hurst指数等级位于3~5级。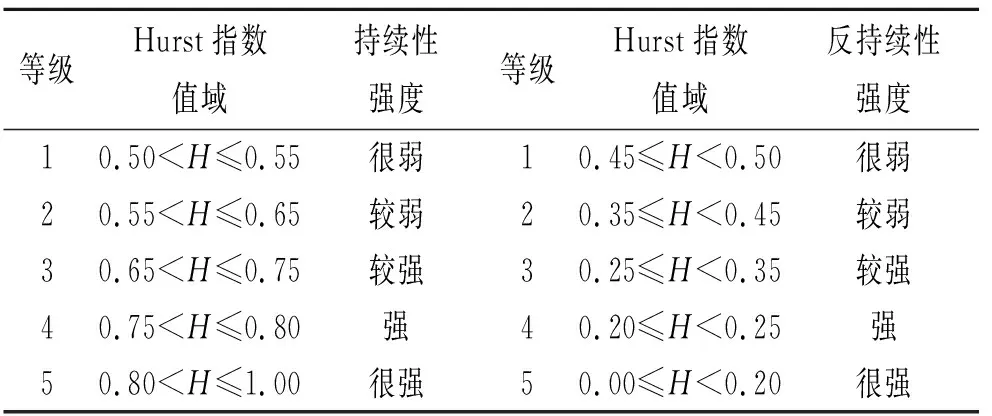
2 结果与分析
2.1 气温变化趋势分析
2.2 气温周期分析
2.3 Hurst指数分析

3 结 论

