矩形薄板受横向均布载荷作用弹性小挠度解*

王 霂，王洪波

（海军士官学校 六系，安徽 蚌埠 233012）

矩形薄板在横向均布载荷作用下的弹性小挠度动力响应是工程中经常遇到的问题。无论是高空建筑中外立面承受风载问题[1-7]，还是舰艇受海浪冲击问题[8-10]，都可以抽象为这一问题。经过一百多年的发展，学界对矩形薄板在横向均布载荷作用下的弹性小挠度动力响应已非常充分。本文在前人研究的基础上，总结梳理了推导矩形薄板在横向均布载荷作用下弹性小挠度动力响应的三种方法，并对三种方法进行了对比。

1 问题的力学抽象

对于不同边界条件的矩形薄板，都可以用四边简支矩形薄板的解叠加边界的弯矩来得到理论解。因此，本文主要考虑四边简支矩形薄板受横向均布载荷作用下的弹性小挠度动力响应。对工程实际的力学抽象如图1所示，考虑一块四边简支，初始静止，几何尺度为a×b×h，弹性常数为E、v的矩形薄板，受到垂直于其特征面的横向均布载荷冲击，这一均布载荷可以是时变的，即可表示为Pd（t）的形式。问题的研究对象是该矩形薄板在此横向冲击作用下的挠度随空间、时间变化的函数。

2 求解动力学响应的理论分析

2.1 强迫振动法

强迫振动法是求解该问题动力学响应应用最为普遍的方法。Navier最早提出了该方法[11]，其基本思想是将板的位移响应设为双正弦级数形式，在预先满足板的边界条件的基础上，通过调整各项系数，使预设的位移响应函数靠近真实响应。

图1 问题的力学抽象

弹性小挠度薄板的控制方程为：

简支边界条件下，Navier解为：

将横向载荷按Navier解的形式展开，得到：

其中，每项系数可以表示为：

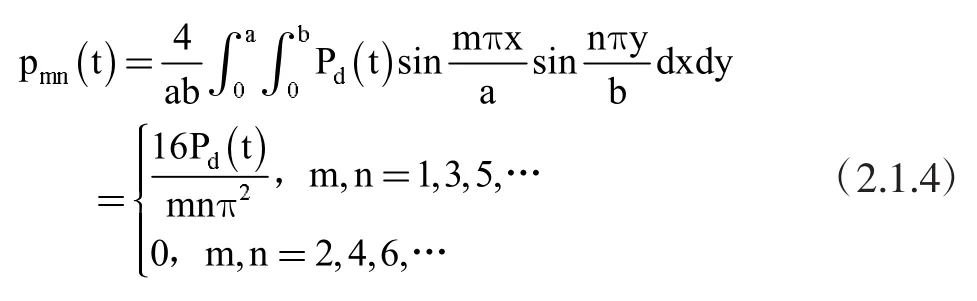
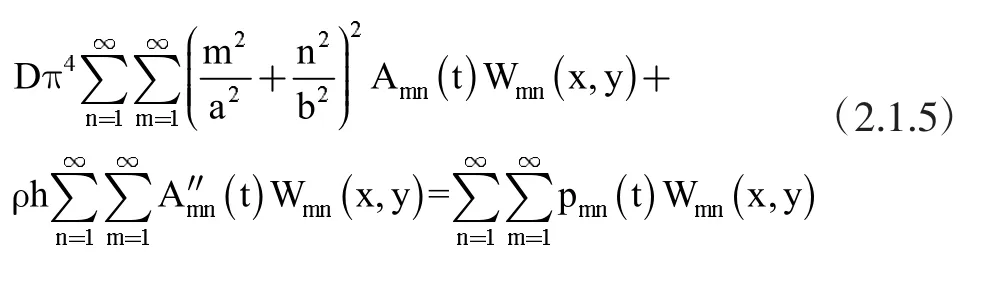
考虑到Navier解各项之间的正交性，可以得到：

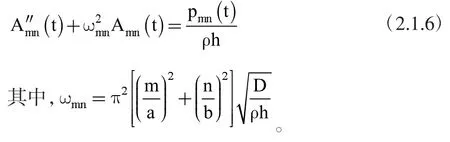
该方程的解为：

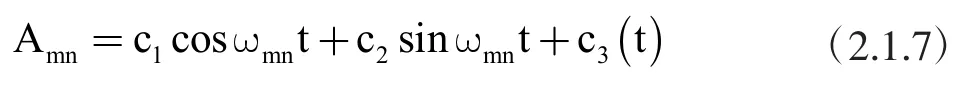
其中，前两项是通解，最后一项为特解。

由初位移和初速度为零的初始条件，有：

对于m、n不全为奇数的情况，方程化为齐次，由（2.1.8），该方程只有零解。

对于m、n全为奇数的情况，可先求出特解，再根据特解求出通解系数从而定解。值得指出的是，如果均布载荷随时间的变化函数性态不好，这一特解不一定有显式表达。对于常见的倒三角型线性衰减时变载荷，不难求出：

其中，p0为初始载荷，td为载荷衰减到零的时刻。

代入初始条件（2.1.8）式，可以解出前两项系数为：

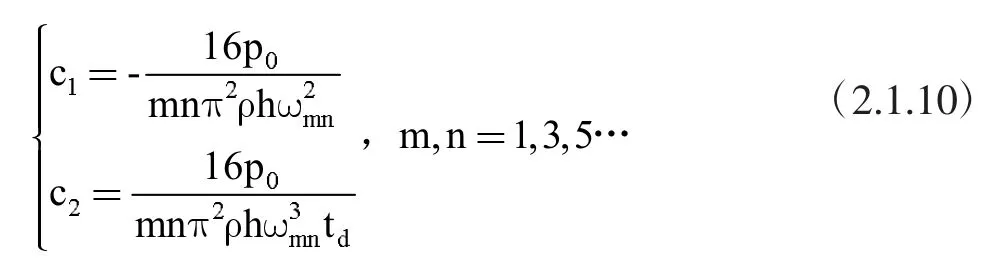
由（2.1.2）、（2.1.7）、（2.1.9）、（2.1.10）即可以得到板内任意一点在冲击过程中任意时刻的挠度。

对冲击结束后的振动，为（2.1.6）的齐次方程，即：

由连续性条件，可以得到其初始条件为：

与冲击过程相同，解是否能显式表达高度依赖于均布载荷的时变函数，对前述的倒三角衰减问题，其解为：

由（2.1.2）、（2.1.11）、（2.1.13），可以得到冲击结束后板内任一点任意时刻的挠度信息。

2.2 能量法

能量法的基本思想非常简单，忽略动力学过程中的各种力学参数的复杂变化，只考虑动力学过程中能量的转化。

简支薄板受到横向冲击时，冲击所做外力功全部转化为板的动能和应变能：

其中，W为应变能密度函数，可以由挠度给出，其关系为：

仍然考虑 Navier形式的解，将（2.1.2）代入（2.2.2），将结果再代入（2.2.1）式，并计算空间上的积分，得到：

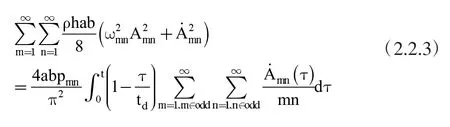
（2.2.3）两边对时间求导，并考虑各项分别相等，得到：

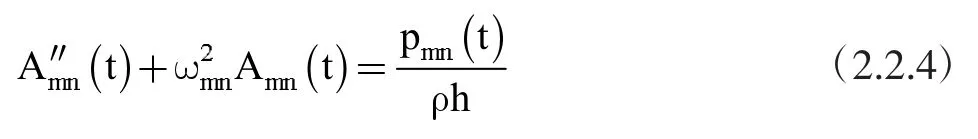
（2.2.4）和（2.1.6）是完全相同的。

同样，如果考虑冲击结束后，板的动能和应变能相互转化，通过类似的计算可以得到：

（2.2.5）实际上是（2.1.6）的齐次方程。

能量法与强迫振动得到的定解方程和初始条件完全相同，最终的解也应该完全相同。

2.3 瞬态振动解叠加法

瞬态振动解叠加法的求解思路是将冲击视为一系列瞬态载荷的叠加，通过卷积计算激励响应。

对初始条件为 w（0）和 w′（0）的薄板，其弹性小挠度无阻尼自由振动的解为：

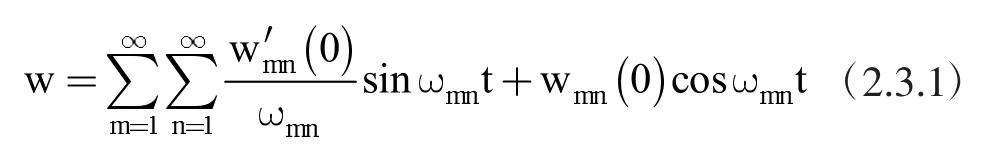
将（2.3.2）按 Navier解形式展开，并代入（2.3.1），得到：

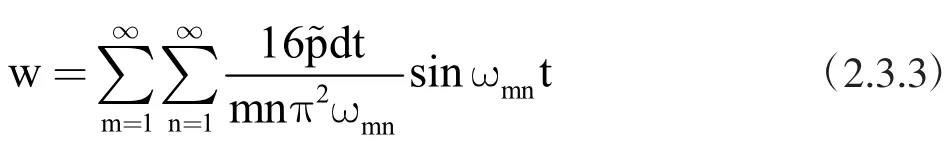
定义响应函数，使其满足：

则可得到响应函数：

将冲击看作一系列瞬态载荷的叠加，可以通过卷积计算激励响应：

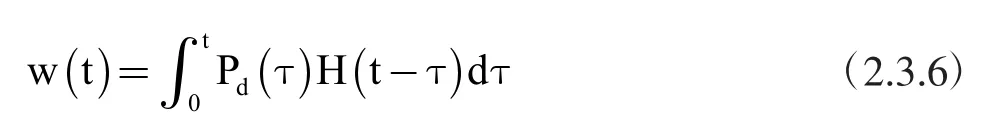
由前述的倒三角型线性衰减的均布载荷，可以得到：

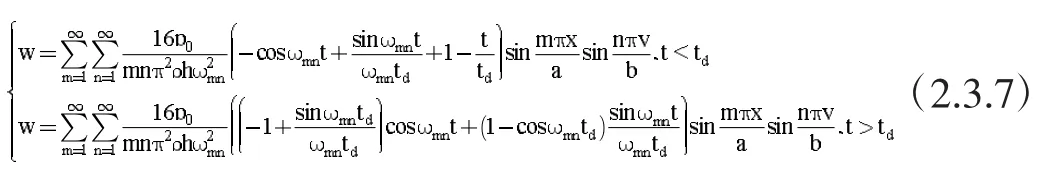
这一结果和前两种方法得到的是一致的。

3 对三种计算方法的讨论

三种计算方法都可以准确得到矩形薄板受横向均布时变载荷作用下的弹性小挠度动力响应。

强迫振动法从薄板的小挠度控制方程出发，逐步求解微分方程，求解思路相当直接，便于理解和掌握，因此在实际工作中应用十分广泛。

能量法则不去计算板内各复杂的力学变量，仅从能量的角度出发，更加便捷地得到了和强迫振动法相同的微分方程。和强迫振动法相比，能量法的思路更加巧妙，数学计算要求偏低一些，但对力学的理解要求更高。

但是，无论是强迫振动法还是能量法，其微分方程的求解高度依赖于时变载荷的积分特性，很难给出微分方程特解的显式解析表达式，进而在后续求解过程中带来较大难度。

瞬态振动解叠加法通过卷积计算激励响应，巧妙地避开了时变载荷积分特性不好带来的数学上的麻烦。即使载荷时变函数较为复杂，也可以表示成形如（2.3.6）的卷积形式，数值上进行积分计算也较为简便。因此，虽然理解该方法难度更高，但在实际工程应用中该方法具有比较明显的优势。