车辆荷载作用下的装配式钢桁架桥应力分析与试验研究

邓 海,许宏伟

(1.石家庄铁道大学 道路与铁道工程安全保障教育部重点实验室， 石家庄 050043；2.石家庄铁道大学 土木工程学院，石家庄 050043)

装配式钢桁架桥是一种能快速架设、撤收，且灵活机动的移动式桥梁。在军事运输、抢险救灾等方面具有重要作用，在平时的交通工程建设保障中也发挥着重要作用。车辆荷载是钢桁架桥承受的主要载荷，桥梁结构在各种车辆载荷的作用下，车辆与桥梁的相互作用将引起桥梁系统的振动，考虑动力效应的内力和变形均大于静荷载作用下的内力和变形。因此分析车辆动荷载作用下的钢桁架桥应力特性具有重要意义。王春平[1]利用ANSYS对钢桁架桥进行了静载分析，并与试验结果进行比对；张筠松[2]同样利用ANSYS软件对钢桁架桥进行了应力时变分析，得到了桥梁应力的时变规律，但没有进行实验验证；陆耀清[3]对装配式钢桁架桥承载力和应力进行计算分析，并对桥梁整体结构的稳定性进行验证。

1 车桥耦合模型及振动方程

合理的车辆模型[4]能适当地体现车辆系统的振动特点，又不明显增加计算工作量。由于研究对象、目的和运行条件的不同，很难建立一个通用的、精确的模型来研究所有车辆动力学问题。当一个实际振动系统较复杂时，建立的模型越复杂，越接近实际情况，也越能进行逼真的模拟，但是往往分析困难；建立的模型越简单，分析越容易，但得到的结果可能不精确。针对本次研究，采用带有两条履带的60 t履带荷载作为车辆荷载，其中每一条履带都可以简化为移动的均布质量如图1所示。

图1 移动均布质量作用简化模型示意图

车辆模型的振动方程[5]为：

(1)

假设履带在运行的过程中始终与桥面密贴不脱离，则使得车桥成为一个系统，履带的位移可通过梁的相应位移表示，其方程成为联系方程，即：

ui=zi-(-dri)-yi

(2)

其中：zi表示车辆第i个履带由静平衡位置起算的竖向位移；dri表示行车路线的外形(dx)在作用点处的坐标；yi表示桥梁在第i个履带作用下的瞬时变位；ui表示为车辆各轴悬挂弹簧与桥面间相对位移。

此时将zi代入向量{Zv}中，可得到由ui组成的表示车辆与桥梁相对位移的向量{Uv}，相应的对时间一次导数，二次导数向量代入方程(1)中得到车桥为一个系统时的车辆振动方程。

将车辆和桥梁视作两个分离体系，二者之间耦合作用[6]通过履带与桥面间的相互作用联系起来。履带与桥梁间的相互作用力描述为：

(3)

式中：Ki1表示第i个履带的刚度；ci1表示第i个履带的阻尼系数；ui表示第i个履带与桥梁的竖向联系位移。此时将Fi1代入方程(1)的向量{Fbv}中，得到车辆和桥梁耦合作用下车辆与桥梁位移的相互关系。

2 有限元模型的建立

有限元分析采用ANSYS通用有限元软件。模型中上下弦杆采用beam188单元，其余杆件采用杆单元Link8，采用参数化建模[7]，以长度52米的桥进行了分析计算。建立模型时不考虑桥面板，两端各留出两米作为支撑，荷载不考虑偏心。得到的桥梁整体模型如图2。

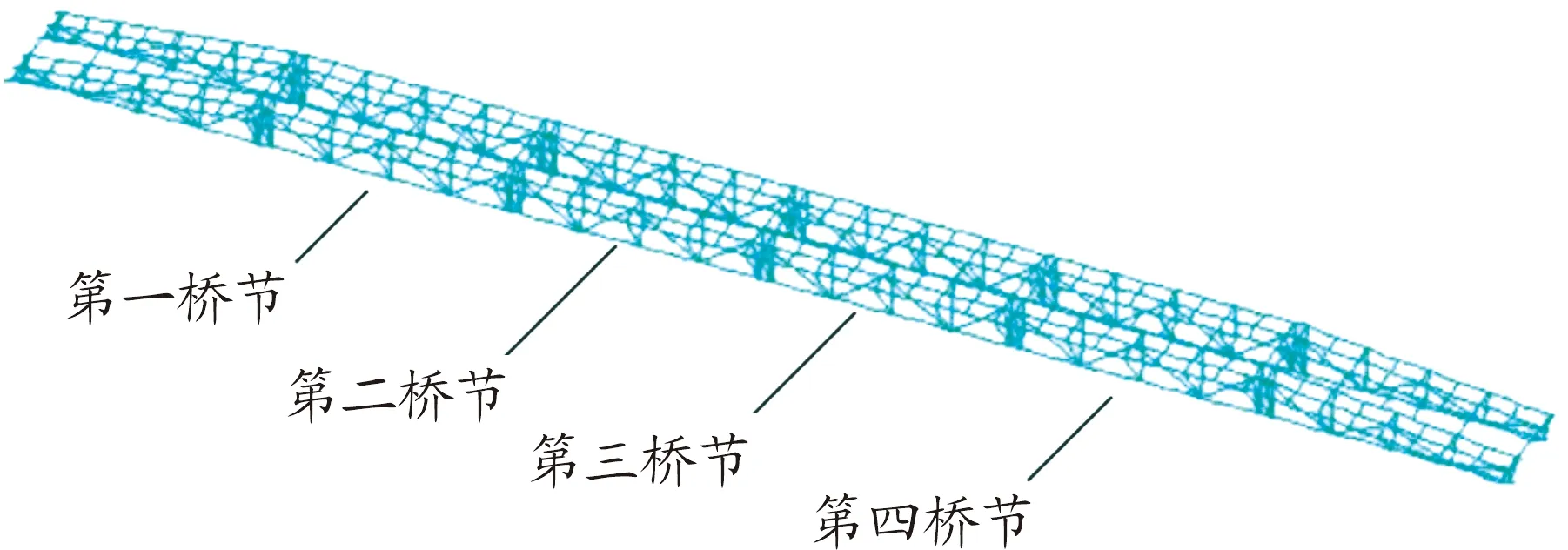
图2 桥梁整体模型示意图

模型中桁架杆件一共有五种，三角形桁架中上部弦杆的两侧(上弦杆1)和中间弦杆(上弦杆2)、下弦杆、斜腹杆和直腹杆，各杆件结构示意图如图3。

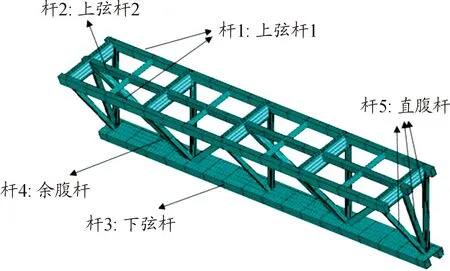
图3 各杆件结构示意图

桁架杆件材料采用特殊DB685钢，σs=590 MPa，材料容重为7.85×10-5N/mm2，弹性模量为2.1×105N/mm2。桥节之间共用节点采用柔性的耦合连接，用以传递桥节之间的作用力，而忽略连接处的刚性损失。

3 数值计算结果分析

依据桥梁实际使用情况，选取重量为60 t的履带式车辆作为通载荷载，含有两条左右对称的履带，履带之间的距离为2.8 m，通载速度考虑5 km/h、10 km/h、15 km/h、20 km/h、25 km/h五种情况。通载过程中，分别提取第一桥节到第四桥节每一种杆件的荷载响应，得到荷载与时间历程曲线。下面以上弦杆1，通载速度5 km/h为例，在提取过程中考虑结构的对称性，选取有代表性的杆件，得到轴力的时间历程曲线如图5。

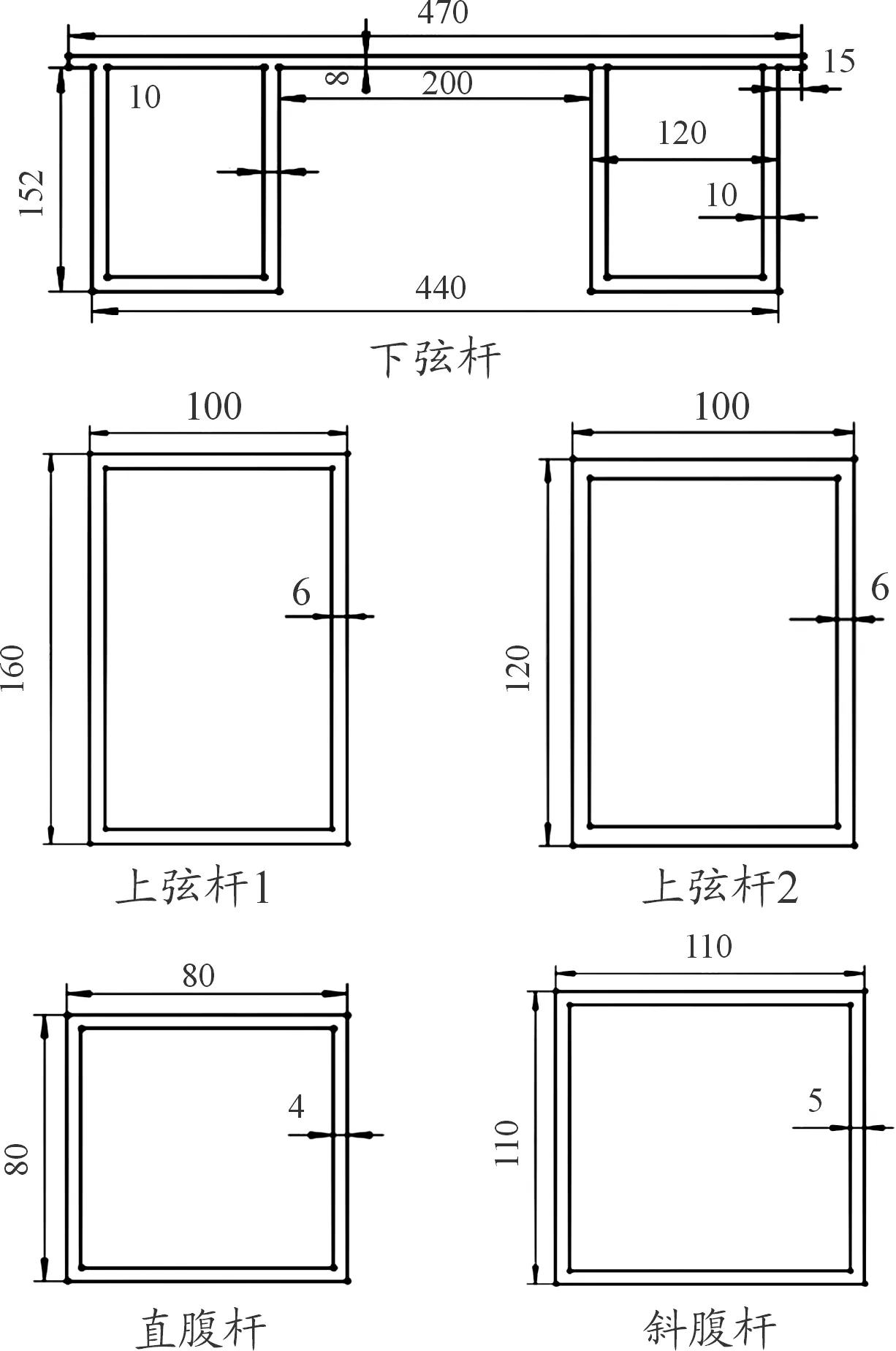
图4 各杆件横截面示意图

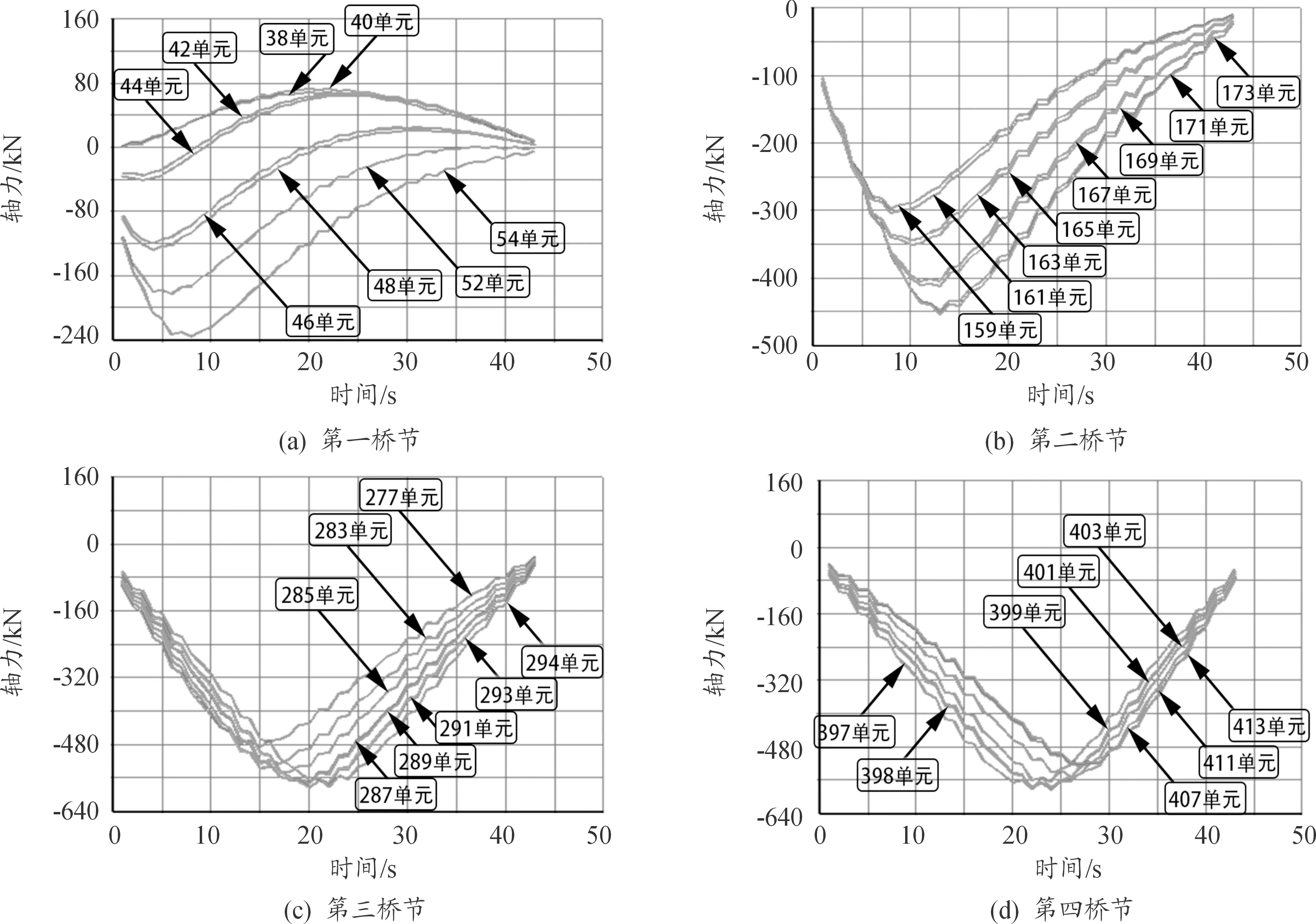
图5 各桥节上弦杆1轴力与时间历程曲线

从图5中可以看出，上弦杆1的荷载与时间历程曲线都呈大致相同的趋势，荷载响应随着荷载位置的移动都是先逐渐增大，然后逐渐减少，在某一位置达到最大值。从上述图可以看出最不利的杆件(荷载最大的杆件)出现在第三跨和第四跨中间位置，也是整桥的中间位置。出现在293、294、397、398四个单元附近，数据如图6所示。

从图6可以看出，上弦杆1的最不利杆件为单元293和398，荷载同为-582 kN，这两个单元的位置相对跨中是对称的，此时的荷载位置为21 m和25 m处。293单元的位置为25.047 m，293单元的位置为25.953 m(均指单元的中心位置)。采用上述方法，可以得到5种杆件分别在通载速度为5 km/h时各自单元轴力时程曲线图以及最大单元轴力，其中上弦杆2最大单元轴力为191 kN，下弦杆最大单元轴力为1 983 kN，直腹杆最大单元轴力为-796 kN，斜腹杆最大单元轴力为-537 kN。由于篇幅所限，相关图文这里不展开论述。

图6 弦杆1四种单元轴力与时间历程曲线

综合以上仿真数据，就可以得到60 t履带荷载通行速度为5 km/h、10 km/h、15 km/h、20 km/h、25 km/h时，5种最不利杆件的轴力时程曲线，如图7。

从图7可以看出，LD-60荷载通行过程中，各杆受力大小均不同，其中杆件3受力最大，其他由大到小依次为杆件2、杆件5、杆件1和杆件4。同时，对各杆而言，随着荷载位置向桥跨中间移动，各杆件受力会逐渐增大；当荷载位置到达桥跨中间位置时，各个杆受力达到最大；随着荷载远离桥跨中间位置，各杆受力又开始逐渐变小。从桥梁动态响应情况分析，通行速度越小各杆受力曲线越光滑，说明桥梁动态响应随着荷载通行速度的增大其波动也增大。这表明随着通行速度的增加，桥梁的高频波动越来越明显。桥梁的频率波动主要受车辆荷载的集中作用力影响，当车辆荷载速度较低时，同一时刻荷载移动的距离较短，桥梁受到集中载荷冲击的次数增加，因此其波动频率越高，反之当车辆载荷速度增加时，频率越小。

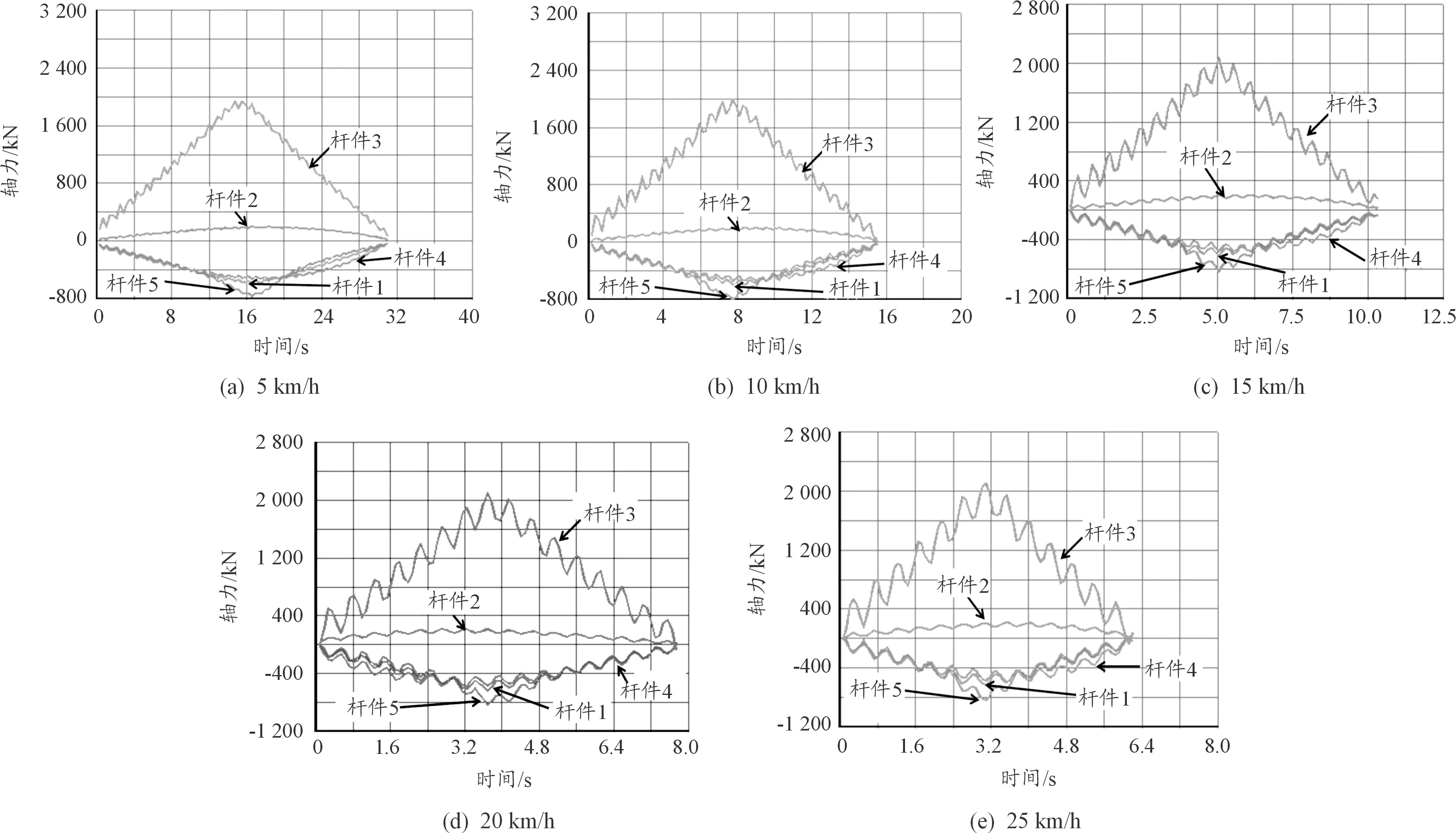
图7 不同速度下5种最不利杆件轴力与时间历程曲线

为进一步分析通行速度对各杆受力情况的影响，可从各杆轴力时程曲线进一步得出各杆最大轴力与通载速度的曲线，如图8。

图8 不同通载速度下的各杆最大轴力曲线

从图8可以看出，通行速度从5 km/h增大到25 km/h时，各杆件所受的最大轴力都略有增加，但增加幅度不明显，最大轴力尚在承受范围之内，因此可以初步验证桥梁承载力设计满足使用要求。

4 验证

应变测量采用DH5907无线动态应变测试系统。由于桥梁杆件相连以及桥跨相连的连接销处容易产生应力集中，因此应变片实际布置如图9所示。

图9 测点位置布置示意图

通行荷载以恒定速度进行通载，各往返通载3次，采集桥梁通载过程中的动态应变数据求取平均值。为保证了测试结果的可靠性，各次试验的间隔时间超过10 min，以使结构变形恢复。试验中考虑到试验的安全性，荷载通行的实际速度为：3.5 km/h，其与最初数值计算参数存在差异，为更好的验证数值计算的可信性，对实装试验的实际工况也进行了数值分析。有限元计算值与试验测试值见表1。

表1 各测点的应力最大值

从表1可以看出：总体而言，试验结果与数值计算得出的各测点的最大应力值吻合较好，但试验的结果比仿真计算的结果要大，分析原因主要是实装试验过程中难以严格保证荷载通行过程中是沿桥梁的中心线行驶，或大或小存在偏载，导致部分测点的测量结果偏大；同时，实装试验中对称布置测点的实际测量结果存在差异，分析原因既有荷载偏载的因素，也有实际操作误差的影响因素，特别是在贴应变片的环节难以达到理论要求。相较而言，数值分析中对称位置的计算结果则较为一致。数值分析结果与实装试验结果的相对误差最小为2.3%，最大为10.5%，平均误差为7.1%，除去一些客观不利因素影响，可以看出本文建立的计算模型是合理的，采用的数值计算方法可行的。

图10给出了各测点位置实验测量值与仿真计算值的对比曲线，可以看出，数值模拟值与试验值得整体变化趋势一致，两者之间的差值在误差范围之内。最大应力点出现在Q11和Q15位置上，从桥梁结构上看，下弦杆作为主要的承力杆件承受最大的弯矩作用，两个测点都位于下弦杆外侧部位，与载荷作用中心的距离最远，受到最大的扭矩作用，因此这两个部位的结构是结构优化中的关键部分。

图10 各测点实验与仿真最大应力值对比

5 结论

1) 利用ANSYS建立了装配式钢桁架桥有限元模型并进行了仿真分析，得到了桥梁在不同通载速度的车辆荷载作用下，各个杆件最不利单元的轴力时程曲线以及各杆最大轴力与通载速度曲线，为桥梁进一步结构优化提供了仿真依据。

2) 进行了应力试验测试，测试值与仿真值的相对误差最小为2.3%，最大为10.5%，误差范围符合要求。说明基于ANSYS建立的有限元分析模型能够正确反映桥梁的实际受力情况，仿真计算分析可靠。

3) 分析得到了杆件最大轴力随通载速度的增大而增大，桥梁的动态响应波动也随着荷载通行速度的增大而增大，为制定桥梁的通行规则提供了仿真依据，限定通行载荷的速度。