误差传递公式的教学探索
蔡丹 杨涛 陈国华
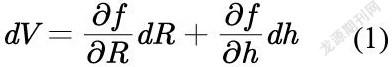

摘要:误差分析是大学物理实验中的一个重要环节,但学生常因对误差传递公式的理解不透彻而无法正确的对实验结果进行误差分析。针对这一问题,本文在结合具体学情的基础上,对误差传递公式这一知识点的教学方法进行了探索研究。
关键词:误差传递公式;教学探索
前言:在大学物理实验中,最终的测量目标都是间接测量量。间接测量的结果是由直接测量结果按照一定的表达式计算出来的。因此,直接测量结果的误差(或不确定度)就必然影响到间接测量结果,这种影响的大小也可以通过相应的表达式计算出来,即误差传递公式(注:误差传递公式(error propagation formula)是2019年经全国科学技术名词审定委员会审定发布的物理学名词)。
误差传递公式是误差分析的基础,同时也是教学过程中的重点和难点。理工类专业的学生,学习大学物理实验课程的目标不应局限于仅仅掌握相关的实验操作技能以及正确的测量数据方法,还应该能够正确的进行数据处理和误差分析,给出合理的实验结果,明确主要误差的来源。从而在后续的设计性实验中进行误差分配,正确选择仪器。
一、学情分析
大部分国内高校开设的大学物理实验课程在第一次授课时,都会专门安排一节绪论课,对物理实验中的基本操作常识、仪器用法和误差理论进行讲解。由于误差传递公式是误差分析必不可少的工具,也被放到了绪论课中。但在后续进入具体实验项目之后,教师们一般都不会再花时间对相应实验中所用的误差计算公式进行推导或解释。因此,如何在上绪论课时就将这个贯穿始终的知识点讲解明白,就显得十分的重要。
然而作者在多年教学过程中感受到,很多学生并没有很好的理解和掌握误差传遞公式,即便记住了公式却也“知其然,不知其所以然”。相应的,在学生所上交的实验总结报告中,误差分析部分通常总是完成得最不理想的部分。可见,如何改进教学方法,使学生学得好,教师容易教,便是迫切需要解决的问题。
本校选修大学物理实验课程的通常都是大一下学期及大二上学期的理工科专业学生,作者通过调查发现,在讲解绪论课时大多数专业的学生正在或者刚刚学完高等数学课程中关于多变量微积分的章节。俗话说:“数理不分家”,于是作者尝试在讲解误差传递公式时,将数学知识与物理实验更紧密的联系起来,让学生从多个角度去认识和理解误差传递公式,从而更好的掌握这个重要的知识点。
二、教学设计
我们不着急按照教材推导误差传递公式,而是首先通过一个简单的例子来说明,直接测量的误差(或不确定度)是为何,以及如何传递到间接测量的结果上。
[例1] 圆柱体的体积,为了测量,需要先测量出和,即圆柱体的底面半径和高。
这里把体积写成自变量为R和h的二元函数,即。显然,和的实际值决定了的实际值;而若和的测量值偏离了它们的实际值,也会引起的计算值偏离其实际值。我们知道,为了考察自变量的微小变化如何影响因变量,可以通过求微分来实现,由于这里的是二元函数,所以应该用全微分,即:
在高等数学中,微分代表的是变量的变化量。而在物理实验中,某个变量在一定的范围之内变化又可以理解为其真实值存在着一定的不确定度,或者说误差。因此,我们将上式中的微分号替换为代表不确定度的,即
如此,我们就建立了一种把直接测量的不确定度与间接测量的不确定度相关联的表达式,也即误差传递公式。但是,若用上式进行不确定度的计算,可能会因为右端各项之间正负抵消,导致对测量结果不确定度的估计过于乐观。因此,很多教材中将误差传递公式定义为:
可见,和的不确定度都会对的测量结果产生影响,而两者的影响力取决于各自偏导数的大小。
结语
数理结合的教学设计,在一定程度上降低了学生对于误差传递公式的理解难度。问卷调查显示,超过80%的学生表示理解并容易接受上述“三步走”的推导过程。对比分析后发现,采用新教法授课的学生,其实验总结报告中误差分析部分的正确率有了明显的提高。当然,学生的学情、课程设置、课程要求等都是动态变化的,需要在教学过程中不断地进行探索和创新。
参考文献
[1]陶绪德.任意函数误差传递公式教学的处理[J].物理通报,1997(01):11.
[2]张建方.关于误差的传递公式[J].数理统计与应用概率,1995(03):57-70.
[3]朱正华,黄建刚,吴凤英.一个间接测量误差传递公式的普遍证明[J].湖南大学学报(自然科学版),2001(S1):1-3.

