课程安排中的匹配问题及求解

张敏捷

（湖北文理学院数学与统计学学院 湖北·襄阳 441053）

为保障教学质量，各级各类的学校都要结合自己的师资力量，合理地安排教学，尽最大的努力让学生受到最好的教育。因此，在现有师资条件下，如何合理地安排教师进行课程教学，具有重要的研究意义。

例如，某学校某教学部，要安排n位教师负责n门课程的教学工作。为尽量减轻教师的教学负担，要求每位教师负责一门课程的教学工作。如何安排可以达到最好的教学效果？

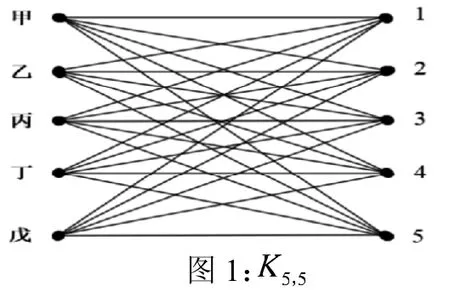
将每位老师和每门课分别用一个点表示，若某位教师能承担某门课程的教学，则将对应的两个点连边。同时可基于各位老师以往负责各门课程的教学效果，对这些边进行赋权。为方便讨论，不妨先假设每位教师都有承担这n门课程教学的能力。此时，可得到2n个顶点的赋权完全二部图，而此时课程安排问题便可以看作求赋权完全二部图的最大完美匹配问题。

例：某校某学期要安排五位教师甲、乙、丙、丁、戊承担五门课程的教学任务。根据近五年的学生评教，统计出各位教师负责相关课程的平均成绩，如下表所示。若以此为依据安排教学任务，如何安排，可使教学质量最好？（假设每位教师负责一门课程的教学任务。）

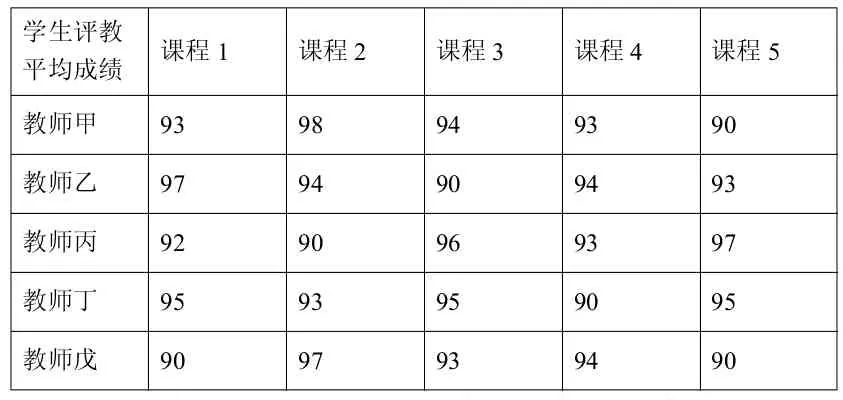
学生评教平均成绩 课程1 课程2 课程3 课程4 课程5教师甲 93 98 94 93 90教师乙 97 94 90 94 93教师丙 92 90 96 93 97教师丁 95 93 95 90 95教师戊 90 97 93 94 90

解：首先，将此问题转化为最小完美匹配问题。写出此问题对应的效益矩阵A，

注意到矩阵A中最大元是98。分别用98减去矩阵A中各元素，得到矩阵C。不难验证，求解以A为效益矩阵的最大完美匹配问题等同于求解以C为效益矩阵的最小完美匹配问题。

事实上，我们可以先将矩阵C的各行各列减去相应的最小元素，即

因此，我们可以得到如下最优方案：教师甲负责课程2，教师乙负责课程1，教师丙负责课程5，教师丁负责课程3，教师戊负责课程4。此时总评教成绩为：98+97+97+95+94=481。

以上，我们将课程安排问题转化为了二部图的最大完美匹配问题，并利用匈牙利法对其进行了具体的求解。下面，我们给出关于此问题的几点思考与推广：

（2）按照上述方法寻找“0”时，若在某一步发现对应的矩阵中含“0”最少的行或列至少含有2个“0”，则说明最优方案并不唯一。我们不妨将上述例题中的数据稍作修改：将教师丁负责课程3的学生评教平均成绩由之前的“95”改为“94”。重复上述过程可得

此时，我们就会自然而然地考虑：到底有多少个最优方案呢？通过上述过程，不难发现，确定最优方案的个数等同于寻找矩阵中位于不同行、不同列的5个“0”的组数。而这个问题又可以转化为求其补矩阵的积和式的问题。在文献[3]中，钟守楠教授和高成修教授给出了矩阵的补矩阵及其积和式的定义：

定义1：将矩阵M中“0”改为“1”，非零元都改为“1”，所得矩阵称为M的补矩阵。

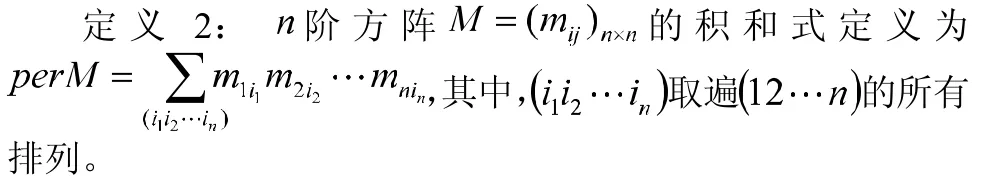
由定义2发现，方阵积和式的定义与方阵行列式的定义极为相似，只是在各项前面不用考虑正负号了而已。因此，计算矩阵积和式最有效的方法便是利用行列式计算中按行（列）展开的思想进行的，我们也通常通过按某一行（列）展开来计算方阵的积和式，只需注意展开时需要考虑该行各元素乘以对应的余子式之和，而不是代数余子式。

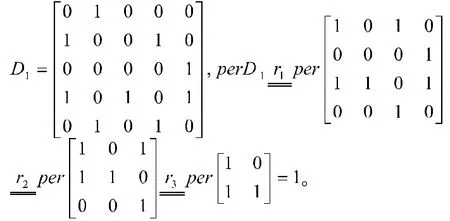
（1）值得注意的是，对于效益矩阵或C者经过上述变形后的效益矩阵，如果其补矩阵的积和式为0，并不能说明这个问题没有最优方案。站在枚举的角度思考，此问题等同于在5种可能的方案里面找最优方案，故最优方案是一定存在的。

我们可以采用如下方法：

不妨在上述例题中，将教师丙负责课程2与课程5的学生评教平均成绩对调，即教师丙负责课程1-5的学生评教平均成绩分别为 92，97，96，93，90。重复上述过程可得：

（2）此问题可考虑借助于Lindo或者Lingo程序来求解。尤其是当教师的人数与课程的门数不相等的情形。具体解决思路值得进一步研究。

致谢：

感谢国家自然科学青年基金（No.11901179）的资助；感谢湖北文理学院科研启动基金的资助。