远海多岛礁战储物资补给优化模型

杨辉跃，杨康辉

（1.陆军勤务学院 军事物流系，重庆 401331；2.中国空气动力试验研究与发展中心，四川 绵阳 621000）

1 引言

远海岛礁对维护国家海洋权益的战略作用日益凸显，岛礁建设、勤务保障成为关注热点。然而，远海岛礁位置分散、离陆地较远，各岛礁的承载能力有较大差异，因战略地位和作战任务不同，各岛礁的物资消耗量和需求量也各不相同，给战储物资的保障带来较大挑战。如何制定合理有效的战储物资补给保障，具有重要的研究价值和现实意义。

针对远海岛礁战储物资保障问题，现有研究主要集中在单个岛礁或单一类型战储物资的保障对策、物资消耗预测和保障体系等方面[1-2]。文献[3]分析远海岛礁物流保障需求，探讨远海岛礁军事运用物流保障体系；文献[4]运用最小二乘支持向量机，对远海岛礁战储物资消耗进行了预测；文献[5]针对战时多目标物资保障任务，建立规划模型并设计了启发式算法求解；文献[6]针对战时单目标需求，建立战储物资调度模型并利用模糊算法和线性规划进行了求解；文献[7]针对战时单周期的远海岛礁保障任务，建立了战储物资供应保障任务多目标规划模型。本文针对远海多岛礁的战储物资补给问题，综合考虑各岛礁承载能力、物资消耗和储备要求、运输方式、物资类型等约束条件，建立保障规划模型，并针对算例给出1周的补给方案，从而为解决远海岛礁战储物资补给问题提供参考。

2 模型准备

2.1 问题提出

现有多个远海岛礁Di需要战储物资补给，各岛礁的物资储备能力和每日消耗量均不同，要求对各岛礁的弹药、航材和油料三类战储物资进行补给。为保证战备需要，战储物资的储存量不少于各岛礁储存容量的a%，各岛礁均建有机场和港口，补给方式有运输机和运输船，但运输机的数量、最大载重、货舱规格和运输船的数量、最大载重、航行速度等有限制；运输船和运输机均从同一物资保障中心出发，每架运输机每天只能保障1次补给飞行，油料只能通过运输船补给。现要根据各岛礁的战储物资消耗量，综合考虑各岛礁的相对位置、最大存储容量、各类物资现有量、日消耗量以及补给方式制约和经济成本等因素的情况下，给出各岛礁的战储物资优化补给方案。

2.2 问题分析

各岛礁的战储物资补给方案涉及补给方式、时间、线路以及物资种类、数量及装载方式等，即该问题需要明确的决策变量，具体包括：

（1）补给方式，即采用运输机补给还是运输船补给；

（2）补给时间，含运输机、运输船出发时间、各岛礁补给时间；

（3）补给物资种类、数量，包括运输工具装载种类和数量、各岛礁补给种类和数量；

（4）补给路线，即运输机或运输船1 次补给的岛礁数、路线规划等。

该问题方案目标是在满足任务约束、条件约束的前提下，补给的成本最低，即最少的补给次数。

补给方式中，运输船速度较慢但运载能力好，主要用于常规补给，运输机补给能力偏弱但运输速度较快，可实现快速补给，运输船可不考虑体积约束；在需要补给的3 类战储物资中，航材存储容量较小，补给要求通常比较紧急，需要采用运输机+运输船的方式，但主要依靠运输机补给，液体油料只能依靠运输船补充。

3 模型建立

根据上述分析，假设：运输机和运输船完成补给任务后立即返航，不在海上或岛礁逗留；不考虑运输机和运输船在补给港口物资装运时间和在各岛礁物资卸载时间；运输机不运输油料。

建立航空补给保障模型如下：

（1）决策变量。

①运输机的使用次数Numf；

②运输船的使用次数Numb；

③运输机第k类航材和第c类导弹的装载量；

④运输船油料，第k类航材和第c类导弹的装载量；

⑤运输船的运输路线，出发日期；

⑥第m天运输机为岛礁Di第l类物资的补给量；

⑦运输机为岛礁Di第l类物资的补给量。

（2）优化目标。

①使用尽量少运输机或运输船补给：

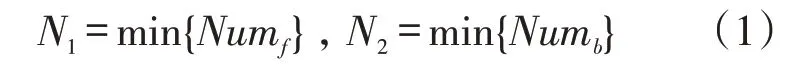
②补给时应尽可能多补充物资，延迟下次补给时间：

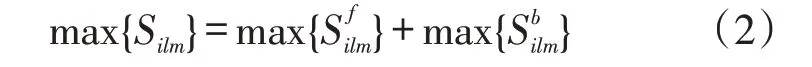
（3）约束条件。

①岛礁Di上各类物资每天的消耗量不超过其日最大消耗量：

②岛礁Di上各类物资每次的补给量不超过其剩余的储存量：

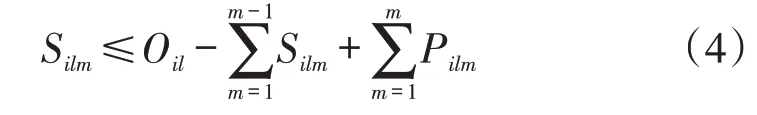
③岛礁Di上各类物资第m天的存储量不少于其最大储存量的a%：

④运输机的体积约束：

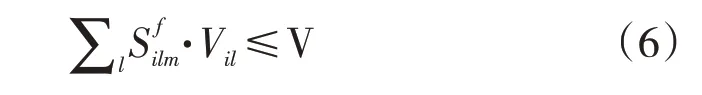
⑤运输机的载重约束：

⑥运输船的载重约束：

⑦各岛礁Di第l类物资第m天的补给量

其中，岛礁Di的第l类物资，l ∈{油料,A1,A2,...,D4,中距导弹,近距导弹}；

Oil为岛礁Di第l类物资的最大存储量；

Pilm为岛礁Di第l类物资第m天的消耗量；

Silm为岛礁Di第l类物资第m天的补给量；

Vil为岛礁Di第l类物资的体积；

Wil为岛礁Di第l类物资的重量；

4 算例分析

设有甲乙丙三个岛礁需要进行物资补给，以甲岛为原点、正北方向为y轴，建立直角坐标系，乙岛和丙岛机场坐标分别为(400km,0)、(300km,300km)，后方补给港口坐标为(600km,1 200km)；有运输机2 架，每架运输机每天只能保障1次飞行，最大载重为40t，货舱规格为长20m、宽3.5m、高3.5m；有运输船2 艘，每艘航速16节（约等于30Km/h），一次可装载1.5万t油料和1 万t 固体物资；需要保障的弹药有中距导弹和近距导弹，中距导弹装箱长320cm、宽40cm、高30cm、重600kg，近距导弹装箱长150cm、宽38cm、高28cm、重110kg；a=50 即各岛礁的战储物资不低于最大存储容量的50%。运输船从补给港口到各岛礁的转运时间，如图1所示。

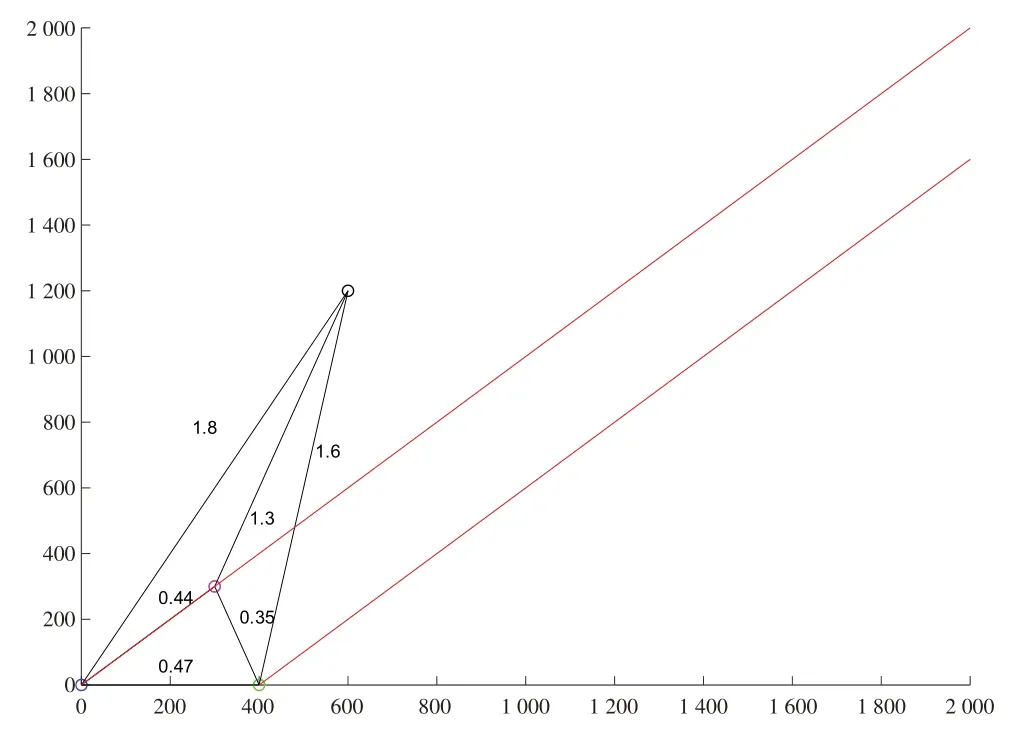
图1 运输船在补给港口和各岛礁之间转运时间

（1）油料补给计算。在最大日消耗条件下，保留战备需求的最少物资，得到各岛礁的最晚补给时间。若运输船直接补给该岛礁，得到各岛礁的最早补给时间，见表1。由表1可知，最大日消耗量远远小于油料的最大存储量，满载油料的运输船一次补给就能满足战备需求，并且无需再次补给。不考虑各岛礁的规模差异，本文补给采用均分策略，尽量延长岛礁的下次补给时间，由此得到各个岛礁油料补给5 000t油料。综合最晚补给时间和最早补给时间，运输船的补给线路可择机安排，出发时间为第一天。

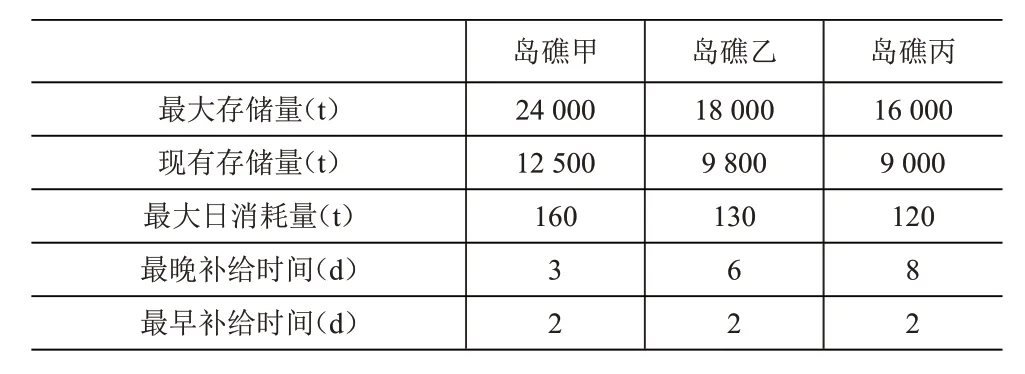
表1 各岛礁油料补给时间分析表

（2）弹药补给计算。各岛中距和近距导弹存储量及日最大消耗量见表2。弹药需要运输机和运输船一起补给，限于运输船的航行时间，运输机必须提供前两天的补给量；运输船到达后按最大存储量补给。在最大日消耗条件下，保留战备需求的最少物资，得到各岛礁的两类弹药最晚的补给时间。运输船对岛礁的最早补给时间是第二天，在运输船补给到达之前，需要通过运输机对各岛礁的弹药进行补给以满足其最低的战备需求。运输船不考虑固体物资体积，载重足够大，一次补给可直接将各岛礁的两类弹药补充至最大存储量，弹药的最大存储量在保证战备需求的同时能满足一周内弹药每天最大日消耗量。运输机第一天必须对最晚补给时间为0 的岛礁的弹药进行补给。

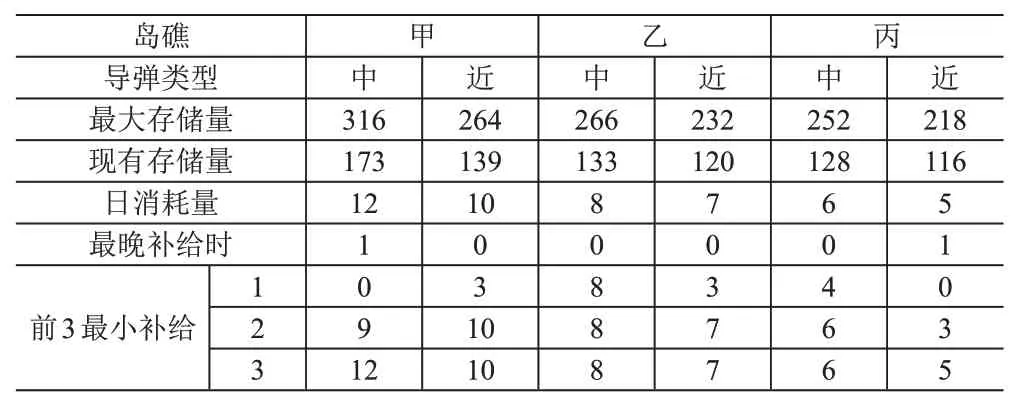
表2 各岛礁弹药补给时间分析表（单位：枚）

运输机的最大载重为40t，货舱体积为245m3，为保证第一天战备物资需求，需补给中距空空导弹12枚，近距空空导弹6 枚，弹药的总体积为5.6m3，总重量为7.85t。为保证前两天战备物资需求，需补给中距空空导弹35 枚，近距空空导弹26 枚，总体积为17.6m3，总重量为23.86t。为保证前三天战备物资需求，需补给中距空空导弹61枚，近距空空导弹48枚，总体积为31.1m3，总重量为41.88t，超过了运输机的最大载重量。

（3）航材补给计算。各岛礁战储航材有4 类16型，甲、乙、丙的寿控件一周每天的消耗情况见表3-表5。根据各岛礁每天的航材消耗情况，首先补给已消耗的寿控件，保证战备最低需求。然后补给存储量最小的寿控件。在满足弹药最大日消耗的同时，在运输机上尽可能多装载航材，使得各类航材能满足战备需求。

表3 甲机场的寿控件一周每天的消耗情况

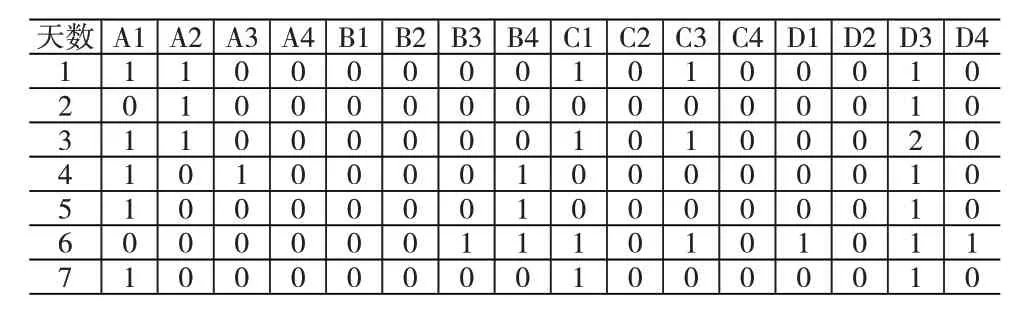
表4 乙方机场的寿控件一周每天的消耗情况

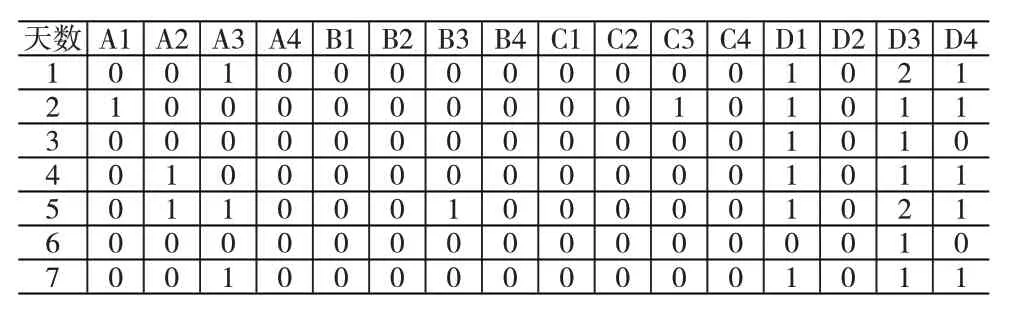
表5 丙方机场的寿控件一周每天的消耗情况

（4）周补给方案。模拟三个岛礁1周的战备物资消耗情况，见表6。利用上述模型，将复杂多变量的优化决策问题转化为背包问题，并利用贪心算法求解，计算给出一种运输机和运输船1 周的补给方案，见表7。

5 结束语

本文针对远海多岛礁的战储物资保障补给问题，综合考虑各岛礁承载能力、物资消耗和储备要求、运输方式、物资类型等约束条件下，建立保障规划模型；设计模拟算例，采用运输船、运输机两类运输方式，考虑三个岛礁的弹药、油料、航材三类战储物资补给问题，在分析各岛礁物资储存量、消耗量与保障能力隐含关系的基础上，通过对决策变量的降维处理，将复杂多变量的优化决策问题转化为背包问题，并利用贪心算法求解，给出了一周的补给方案，验证了补给方案的可靠性和有效性，为远海多岛礁的战储物资补给问题提供参考模型和决策依据。当然，本文对远海保障环境的约束设置不够全面，将使下一步研究的重点。

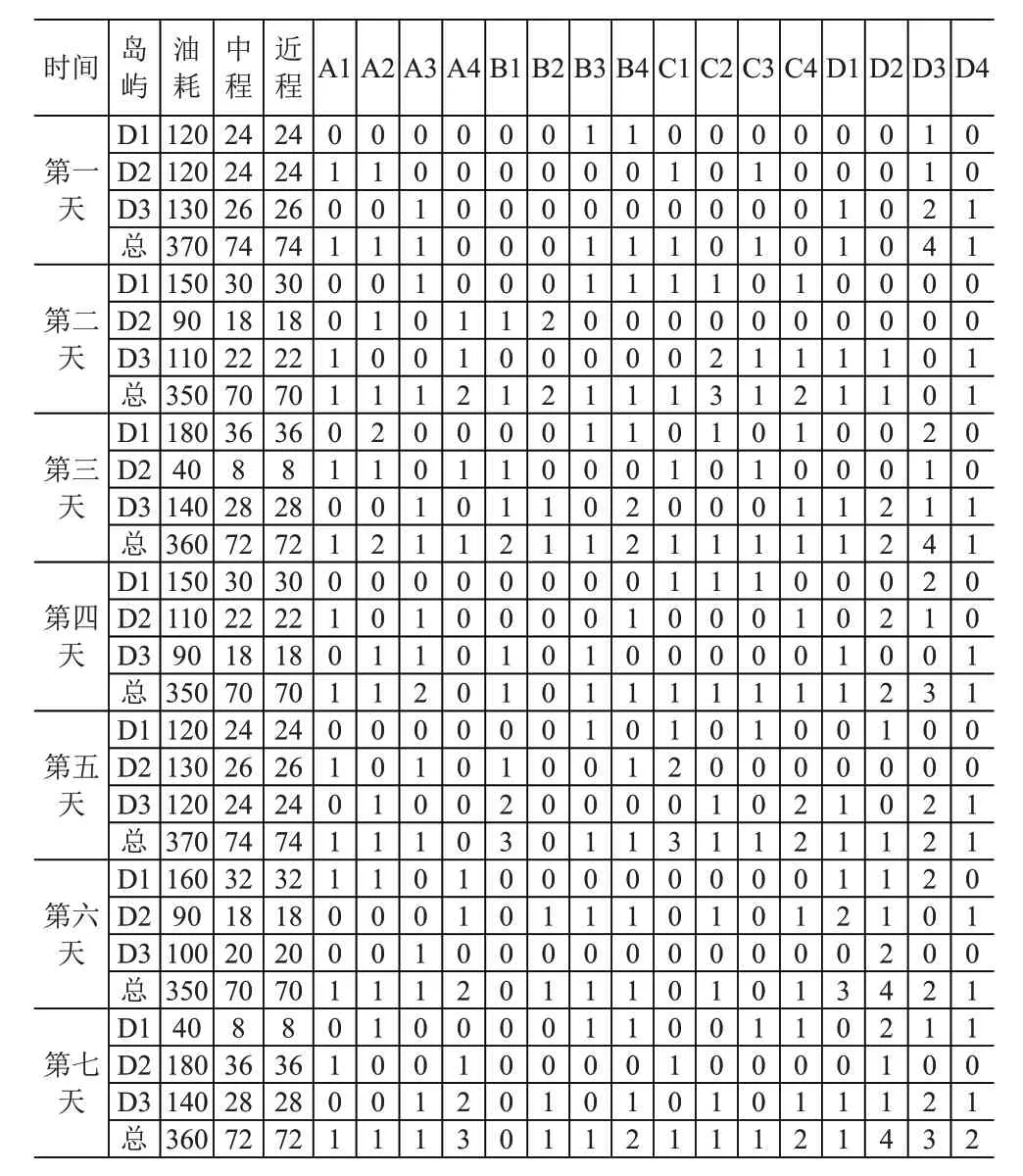
表6 各岛礁一周的物资消耗量

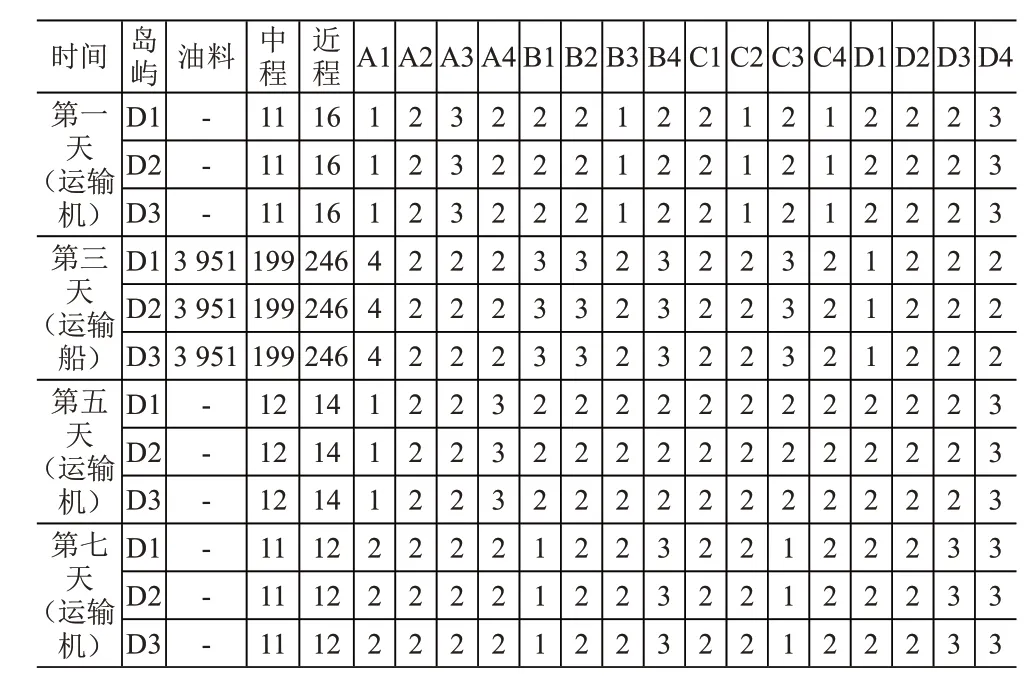
表7 各岛礁一周补给保障方案