基于改进蚁群算法的船舶避碰路径规划决策支持

江冠超 肖英杰 徐笑锋

上海海事大学商船学院

0 引言

随着航运业的发展，船舶逐渐大型化和专业化，航行速度越来越快，并且海上交通环境日益复杂、交通密度日益增大[1]。种种变化带来一个严峻的问题，即避碰决策时间缩短，增加了驾驶员的压力导致作出错误的决策，进而酿成海上事故。解决这些问题有两种途径：一是加强对船员的技术和心理培训，提高船员的素质和技术；二是提高避碰决策的自动化程度，通过实现自动避碰，避免船员主观判断的错误[2,3]。通过技术提高避碰手段，实现船舶自动避碰，减少对主观判断的依赖是解决人为因素问题的有效途径。因此，船舶避碰决策支持系统的研究对船舶安全具有十分重要的意义。

避碰决策支持系统不仅考虑相关的危险和避碰措施，还需要考虑偏离原航线的情况，即船舶避碰路径。船舶避碰路径规划是一个多准则、非线性规划问题，必须在航行安全与经济之间寻求平衡。马文耀等[4,5]提出以船舶避碰转向后至复航回到原航向的航行距离为目标函数，通过算法求出最优的避碰路径。于家根等[6]提出将最近会遇距离和转向角度作为两个目标函数，通过赋予权重构成单一目标函数，通过算法寻找最优路径。曾勇等[7]提出转向角度、航行距离及最近会遇距离构成三个目标函数，赋予权重构成单目标函数。刘冬冬等[8]提出以偏航时间、避碰水域宽度和总航行距离为目标函数的最短避碰路径。刘仁伟等[9]提出考虑风、流及岸壁浅水等环境因素的船舶碰撞危险度量化模型。赵舟等[10]提出以碰撞危险度和转向角度值的负函数表示能够反映决策中避碰安全、路径优化的目标函数。目前大多数避碰路径规划模型没有对安全性经济性量化或者没有考虑复航。蚁群算法在路径规划问题中的应用，需要将规划区域网格化产生坐标点进而转化成类似旅行商的问题[11-15]。在现有的蚁群算法应用中，还不能直接将蚁群算法应用于非线性函数寻优问题。

本文综合考虑前人的研究，分析不足，对以最近会遇距离衡量碰撞危险度和航行距离两个指标进行综合考虑，提出构建随最近会遇距离增大而函数值增大的归一化目标函数和随航行距离减小而函数值增大的归一化目标函数，并量化赋予权重进而构成单目标函数。针对在路径规划中蚁群算法不能直接用于非线性函数寻优问题，提出改进蚁群算法的转移概率公式及信息素更新公式。通过改进的蚁群算法对目标函数模型寻优，得到最优避碰路径参数：避碰转向角度、复航转向角度、复航时间。

1 两船会遇态势

根据《1972年国际海上避碰规则》（以下简称规则），两艘机动船相遇时，其会遇态势分为三种，分别为对遇、交叉相遇、追越，如图1所示。

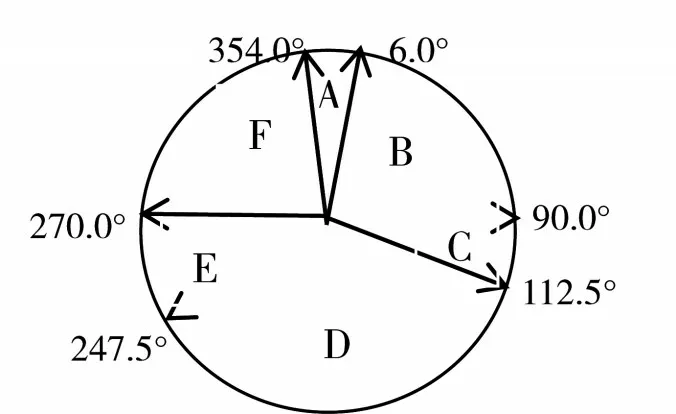
图1 会遇态势

对遇，即两船船首向正在相反或接近相反的航向上，一般解释为左右偏差不超过6°（A 区域）。此时，本船应向右转向。交叉相遇，即当两船船首向交叉时，来船处于本船航向左右大于6°且小于112．5°的方位（区域B、C、E、F）。交叉相遇根据交叉角度，又分为小角度交叉、大角度交叉。区域B、F为小角度交叉，区域C、E 为大角度交叉。根据规则“让红不让绿”，有它船在区域B、C 时且两船构成碰撞危险时，本船应为让路船。追越，即一船从它船正横后大于22．5°的某一方向赶上它船时（D 区域）。此时，追越船应让路给被追越船。

2 转向避碰路径规划模型

当本船需采取行动避碰时，一般通过转向来达到避碰效果。船舶执行转向避碰行动之前会考虑碰撞危险度和航行距离等指标。碰撞危险度与很多因素有关，比如最近会遇距离dCPA、最近会遇时间tCPA、船舶操纵性能以及环境因素等。本文仅考虑最近会遇距离dCPA和最近会遇时间tCPA，忽略船舶操纵性能和外界环境对转向避碰的影响。设避碰决策的目标函数模型为：f=(f1, f2, ．．． , fn)，表示避碰决策与避碰危险度及航行距离等多个子目标函数有关。当目标函数模型取最大值时所对应的参数即为最优避碰路径的参数。

2.1 碰撞危险度目标函数模型

综合考虑国际海上避碰规则和船东利益，船舶最优避碰路径是一条既安全又经济的避碰路径。在安全性及经济性中，安全又是极为重要的因素，因此，首先考虑关于避碰路径的安全因素。衡量船舶避碰后碰撞危险度指标可以用转向后的最近会遇距离dCPA和最近会遇时间tCPA衡量，其值越大避碰效果就越好。如图2 所示，船舶在采取避碰措施时两船会遇距离为D，由刘德新等[16]提出的决策模型可得：

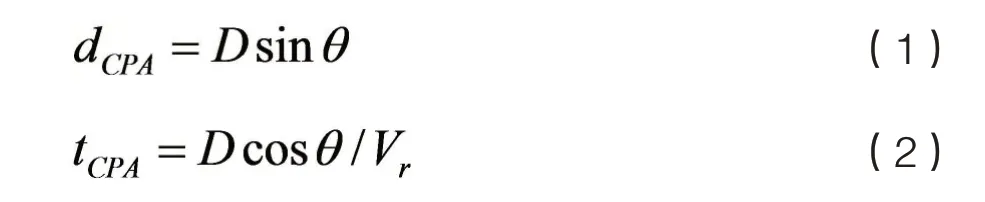
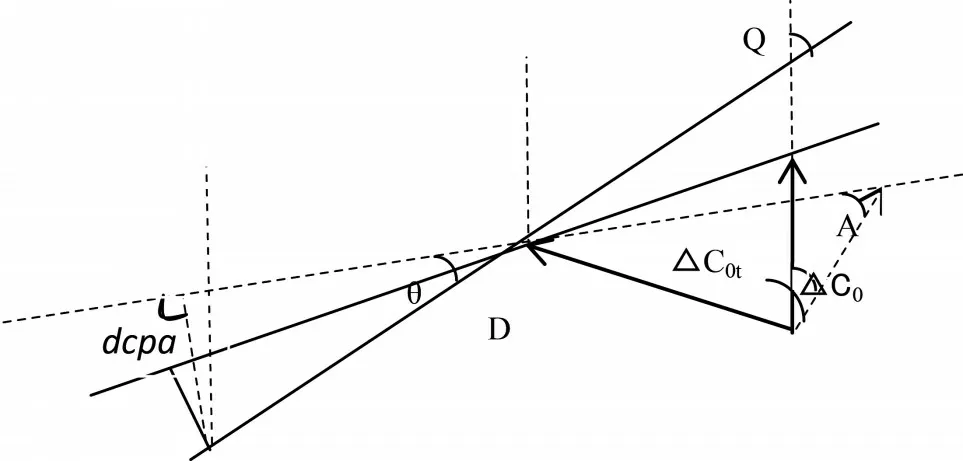
图2

其中，θ 为转向后两船相对运动线与目标船方位线夹角，A为转向后两船相对运动线与本船船首向夹角，△C0t为转向后两船航向线夹角，△C0为本船转向角度，Vr为转向后两船相对运动速度，D 为两船转向后的距离，V0为本船速度，Vt为目标船速度。

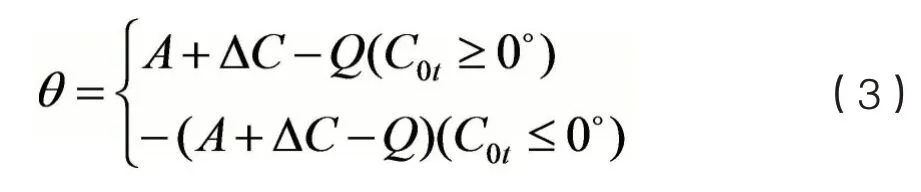
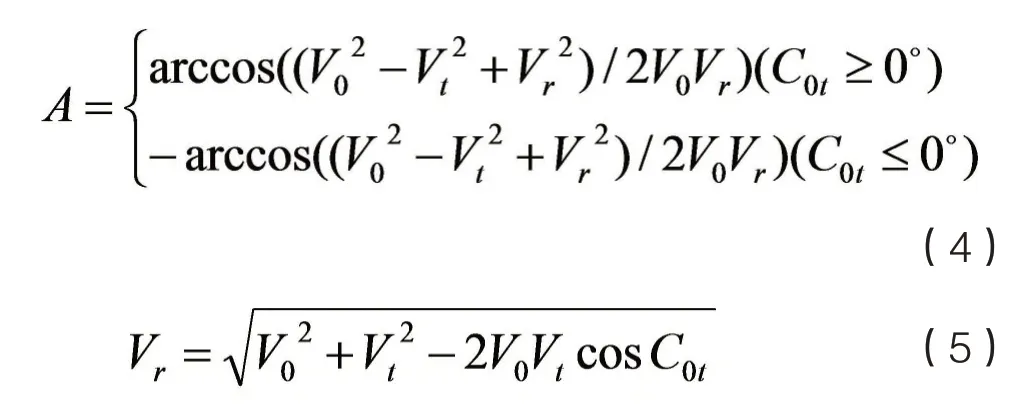
由公式（1）～（5）可以计算得到dCPA及tCPA。

由公式（1）可见，船舶转向避碰后最大的最近会遇距离maxdCPA=D，即θ=90°时。从安全角度考虑，dCPA越大安全性越高，构建两船碰撞危险度目标函数f1：

式（6）中，f1值域为[0,1]，且最近会遇距离越大，其函数值越大。

2.2 航行距离目标函数模型

航行距离指船舶避碰转向后到复航回到原航线上所行驶的路程d。这段路程分为两部分：避碰转向到复航转向的路程d1和复航转向至回到原航向的路程d2。因避碰行动只转向而没有改变速度，设避碰转向角度△C0，复航转向角度△Cr，避碰转向到复航转向时间为T0。则

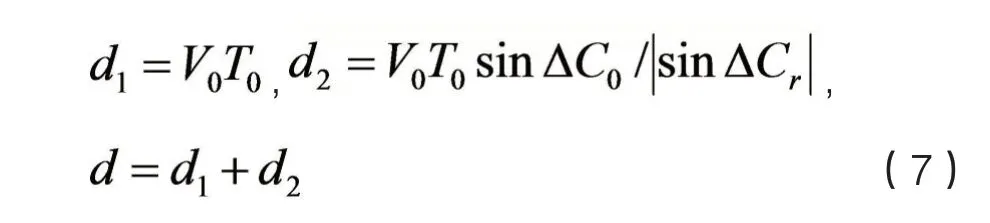
根据规则第16 条规定，让路船应该大幅度行动，综合考虑环境因素以及人为因素，限制以下约束条件：△C0=[30°, 90°]，△Cr=[30°, 60°]，T0=[tCPA1,60 min]，tCPA1为转向后的最近会遇时间。构建本船航行距离目标函数f2：

式（8）中，f2值域为(0,1]，且d 越小，其函数值越大。

2.3 总目标函数模型

所构建的碰撞危险度目标函数及航行距离目标函数的值域都为[0,1],且取值越优函数值越大。若对两个目标函数分别赋予权重α、β（α+β=1），则多目标函数构成单目标函数f：

对f 求最大值，其最大值所对应的参数即为最优避碰路径的参数：避碰转向角度、复航转向角度、复航时间。

3 蚁群算法

3.1 蚁群算法模型

蚁群算法是一种模拟蚂蚁觅食过程的概率型算法，它具有启发式搜索及正反馈信息的特征[10]。它能够求得从原点出发，途经若干个需求点回到原点的最短路径，被广泛应用在旅行商问题。设蚂蚁数量m，点数为n，点与点之间的距离为dij(i,j=1,2,．．．,n)，t时刻i与j连线上信息素为τij(t)、距离启发函数为ηij(t)，由所参考的文献[17,18]可得，t 时刻第k 只蚂蚁从i到j的转移概率为：

3.2 改进蚁群算法

本文所构造的目标函数模型是非线性函数极值寻优问题。从所参考的文献上发现，蚁群算法较多用于TSP 问题及其衍生问题上，即问题需要有坐标点，通过网格化坐标点得到转移概率，进而求出最短路径。受式（10）转移概率公式的启发，在非线性函数寻优问题中，可行解转移概率为：

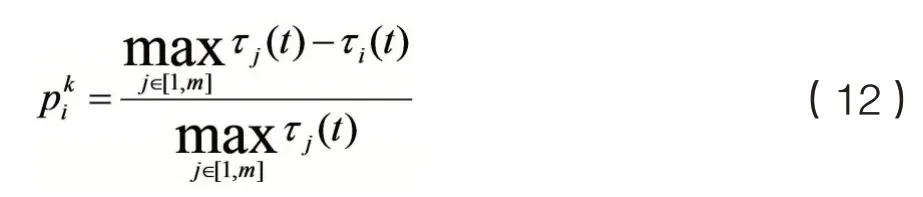
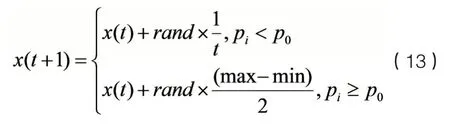
式（13）中，rand为[-1,1]之间的随机数，p0为概率常数，当pi＜p0时，x(t+1)进行局部搜索；当pi≥p0，x(t+1)进行全局搜索。由式（11）信息素更新的启发，在非线性函数求极值问题中，信息素更新为：

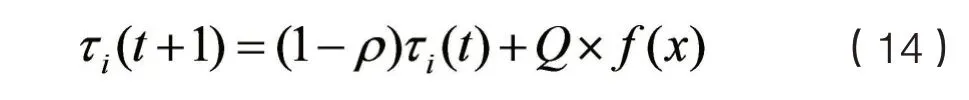
由式（12）、（13）、（14）构造出可用于非线性函数寻优的蚁群算法。

3.3 算法流程

步骤1：将参数初始化。蚁群规模，最大迭代次数，信息素挥发因子，信息素释放因子，转移概率常数，本船与来船航向航速，来船方位等。

步骤2：建立解空间。初始时，对蚂蚁随机分散置于不同位置，然后根据转移概率对每个蚂蚁确定下一个位置。

步骤3：信息素更新。根据信息素更新公式对每个位置信息素进行更新，同时记录当前计算中的最大值。

步骤4：终止判断。若当前迭代次数达到最大迭代次数，结束算法，输出最大值；否则，返回步骤2。如图3所示。

4 仿真实验结果

设本船航速为12 kn，航向000°，目标船航速为12 kn。综合考虑安全与经济的重要性，取α=0．6，β=0．4。根据规则，通过模拟对遇、小角度交叉相遇、大角度交叉相遇三种态势验证避碰模型。为验证算法有效性，避免随机性，重复执行20次算法过程。

对遇：目标船航向180°，方位000°，距离5 nm，其matlab仿真结果显示，除个别值外其目标函数值的范围为[0．581 2, 0．598 3]，最优值迭代过程如图4所示；小角度交叉相遇：目标船航向240°，方位040°，距离5 nm，仿真结果显示，除个别值外其目标函数值的范围为[0．527 1, 0．543 0]，最优值迭代过程如图5 所示；大角度交叉相遇：目标船航向280°，方位050°，距离5 nm，仿真结果显示，除个别值外其目标函数值的范围为[0．415 9, 0．432 1]，最优值迭代过程如图6 所示。三种会遇态势仿真结果，最优目标函数值所对应的避碰转向角度、复航转向角度、避碰转向到复航转向时间、最短航行距离见表1。

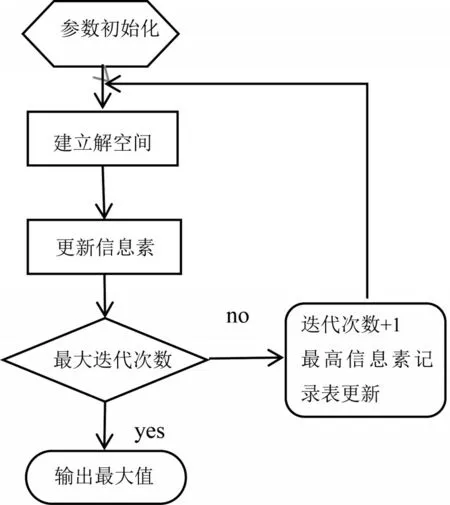
图3 基于改进蚁群算法的目标函数寻优模型

表1 基于改进蚁群算法的最优避碰路径参数

分析仿真结果，此目标函数模型能够在综合考虑安全性与经济性权重后给出最优避碰路径。改进后用于非线性函数寻优的蚁群算法结果可以在迭代50 次内收敛于某一固定值，收敛速度较快；算法运行时间3～6 s，计算速度较快；重复执行20 次算法后，除个别值外，目标函数值稳定在很小的范围内：对遇态势下范围[0．581 2,0．598 3]，小角度交叉态势下范围[0．527 1, 0．543 0]，大角度交叉态势下范围[0．415 9,0．432 1]，此算法可行。

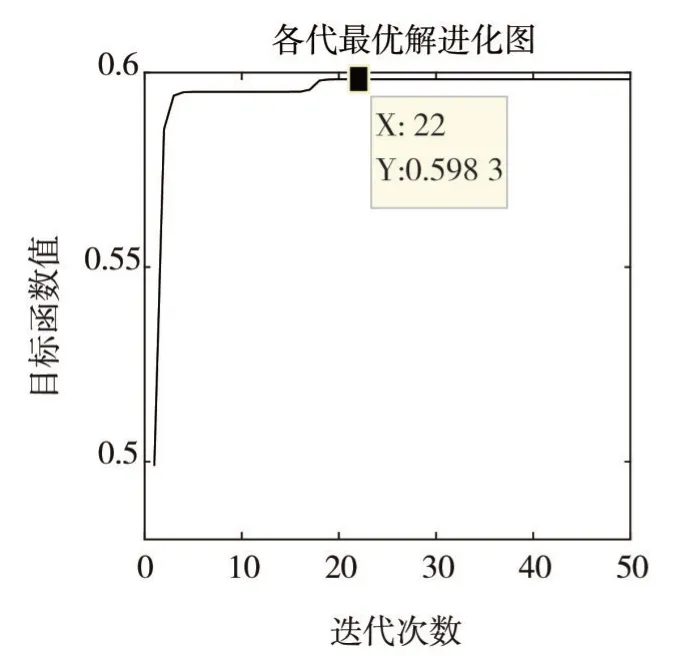
图4 对遇目标函数最优值

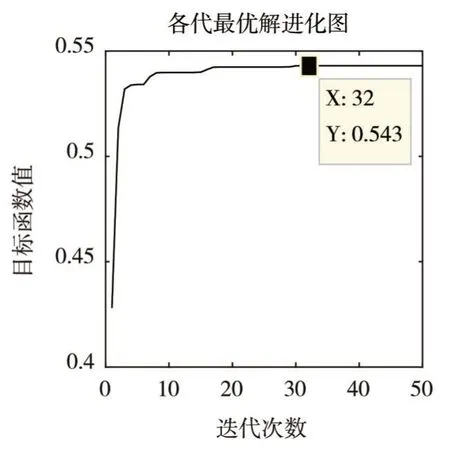
图5 小角度目标函数最优

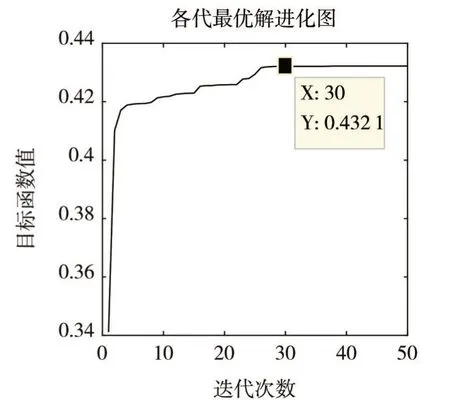
图6 大角度目标函数最优

5 结束语

在开阔水域两船不同会遇态势下避碰路径规划问题中，本文提出一种基于改进蚁群算法的避碰路径规划决策方法。以最近会遇距离指标及航行距离指标建立归一化的非线性目标函数模型，改进蚁群算法的概率转移公式及信息素更新公式。结果表明，改进的蚁群算法在非线性函数寻优中应用效果较佳，迭代过程收敛较快，计算速度较快；综合考虑安全性及经济性权重后，目标函数模型可以规划出最优的避碰路径。此路径规划决策如果能应用在电子海图显示及信息系统中，将有效减轻船员压力，减少海上碰撞事故。