基于FPGA的齿轮测量中心随动控制器设计

何西平

摘要： 为实现齿轮测量中心的随动控制功能，设计了基FPGA的齿轮测量中心随动控制器，该控制器通过增量式PID控制来对测头反馈的示值进行调节计算，使随动轴带动测头运动，最终达到调整测头压入量的目的;通过实验在齿轮测量中心上对该控制器进行了功能验证，实验证明该控制器可以有效的对测头压入量进行调整，可以达到跟踪测量的目的。

Abstract： In order to realize the follow-up control function of gear measurement center， a follow-up controller of gear measurement center based on FPGA is designed. The controller adjusts and calculates the indication fed back by the probe through incremental PID control， so that the follow-up shaft drives the probe to move， and finally achieves the purpose of adjusting the pressing amount of the probe; The function of the controller is verified on the gear measuring center through experiments. The experiments show that the controller can effectively adjust the pressing amount of the probe and achieve the purpose of tracking measurement.

关键词： 随动控制;FPGA;PID;齿轮测量

Key words： servo control;FPGA;PID;gear measurement

中图分类号：TG86                                      文献标识码：A                                  文章编号：1674-957X（2021）24-0149-03

0  引言

目前齿轮测量中心在测量工件时，需要先知道被测齿轮的理论轮廓方程，将测头测得的实际齿面坐标与理论值相比较后，计算出被测齿轮的误差[1-2]。而对于许多齿面轮廓方程未知的齿轮，齿轮测量中心无法进行测量;除此之外，对于被测齿轮的理论轮廓方程已知，但由于齿面磨损、制造等原因导致齿面误差非常大的齿轮，在测量时由于超出了測头的量程，此时也无法进行测量[3]。针对以上两种问题，本课题提出了测头示值的随动控制方法，以FPGA（现场可编程门阵列）开发板为控制核心，通过测头示值的大小来调整随动轴的运动，从而实现自动跟踪测量。

1  系统整体结构

如图1所示为测头示值随动控制的总体控制结构图，主轴和随动轴接收到下位机发送的插补指令后分别进行各自的旋转运动和直线运动，当被测齿轮齿面方程未知或者齿面磨损较大时，会导致测头和齿面接触量发生变化，而使测头示值变化，因此将测头数据经过处理后反馈给随动轴控制器，从而对随动轴的插补指令进行补偿，来调整随动轴的运动速度，使随动轴和直线轴运动速度一致，而将测头示值保持在设定范围内[4]。

2  系统硬件电路设计

随动控制系统的整体硬件电路模块如图2所示。主要在FPGA中对随动轴电路进行了设计，包括偏差计算模块、PID计算模块、测头信号处理模块以及插补模块。各模块的具体设计如图2。

2.1 测头信号处理模块

测头信号处理模块主要对测头示值进行处理以方便偏差计算模块计算，AD977芯片对测头的模拟量进行转换后得到测头的数字量[5-6]，所得到的数字量与AD芯片输入的电压关系如表1所示，可以看出当输入电压为负时，输出数字量用补码表示;当输入电压为正时，输出数字量用原码表示。

为了方便处理，将AD977芯片转换得到的数字量通过中位值滤波算法处理后，滤掉采样中出现的一些奇异值，接着对AD977芯片转换得到的负电压数字量补码形式进行变换，将补码转换成原码。将16位寄存器的最高位做为符号位，前15位做为实际数字量原码形式，当输入为负时，最高位置1，否则置0。

2.2 偏差计算模块

偏差计算模块主要对输入的测头反馈信号进行偏差计算，在偏差计算模块中设定测头跟踪范围为±5um，转换对应的数字量约为±650，因此当测头实际示值超出设定跟踪范围后，偏差计算模块的输出量为实际示值减去设定数字量值，由此可以知道测头的实际状态相对与理想状态之间的差距。

偏差计算模块的采样周期即为系统时钟周期，每隔一个时钟周期对指令数据和实际测头数据进行采样，并求出之间的差值，因此采样间隔非常小，所得到的偏差结果也非常准确。同时为了避免随动轴的响应时间非常大，出现一直发送指令数据，而测头没有响应导致出现机械故障问题，在偏差计算模块中设计了故障提醒信号，当偏差计算模块中的偏差值超过20000时，便将故障信号由高电平变为低电平，同时故障指示灯亮提醒操作者。

2.3 PID计算模块

PID计算模块采用增量式PID算法控制，以下公式（1）是增量式PID控制的算法数学模型[7-8]，其中ek、ek-1、ek-2分别为连续三次采样的测头跟踪误差值，uk、dk分别是PID控制器的输出量和增量，kp、ki、kd分别是比例环节、积分环节、微分环节的系数。

将偏差计算模块的输出量做为PID模块的输入量，并且通过时序电路将输入偏差依此输入到三个寄存器中，产生三次连续采样的输入误差，三个寄存器中的输入偏差之间各相差一个时钟周期，在一开始通过复位信号对三个偏差寄存器进行清零复位，在设定好合适的PID参数后，便可以求出随动控制器的补偿输出量。

由于增量式PID计算模块中的各环节系数可能会取到小数，而在FPGA中不能直接表示小数，只能表示整数，在表示小数的时候，需要将小数用浮点数或者定点数进行表示。使用浮点数表示时设计繁琐并且比较占用FPGA中的数学逻辑资源，但表示的小数相对精确;相反使用定点数表示小数时，设计相对简单便捷，但是不能精确的表示小数，在表示小数时有一定的误差。考虑到在对PID模块各环节系数进行调参时具有不确定性，且各系数的精度误差对输出影响不大，同时考虑到所使用的FPGA开发板资源问题，在不浪费FPGA中数学逻辑资源的前提下，采用定点数来表示小数。

2.4 插补模块

插补模块采用数字积分DDA算法进行直线插补，设计的程序思想如图3流程图所示，在复位信号到来的时候，将被积函数xe、累加次数以及累加函数∑Xe全部清零，将PID的输出量和下位机的指令数据赋值給被积函数，随着时钟上升沿的到来，将被积函数累加赋值给累加函数，当累加次数等于0时停止累加，完成一个位置的直线插补。

在插补模块中，将PID输出的控制量补偿给下位机输出的指令数据，并将累计寄存器∑Xe最高位的溢出作为脉冲产生位，由于插补模块中的被积函数，也就是指令数据和PID输出的补偿数据叠加后的总和，其大小会决定插补脉冲的溢出速度，即被积函数越大，插补输出的控制量变化率越快，溢出的脉冲数越块，从而使插补模块输出的脉冲频率改变，因此通过调整PID输出的控制量大小就可以实现对随动轴运动速度的调整，通过PID输出补偿量数值来调整插补模块被积函数的大小，随动轴的运动速度得到调整，从而达到随动控制的目的，最终让测头的示值始终保持在目标范围内。

3  实验验证

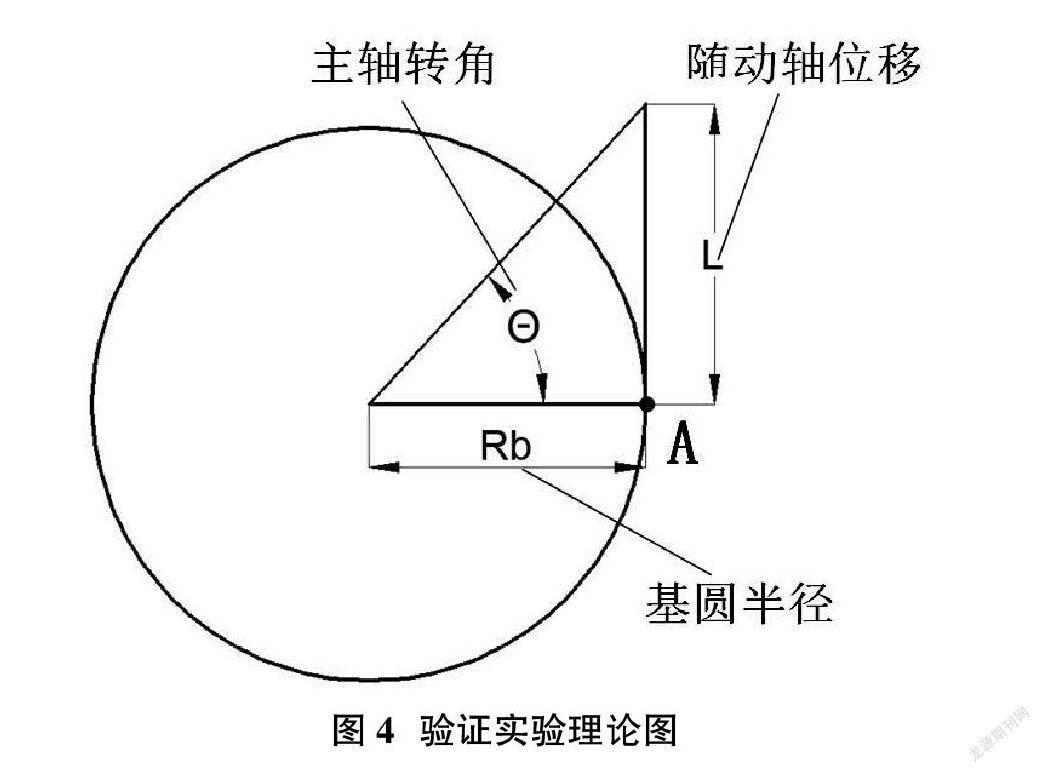
完成电路设计和仿真验证后，在齿轮测量中心上进行了在线对比实验，以参数已知齿轮为工件，如图4所示，将测头调整至被测齿轮基圆切线附近的A点，由主轴转角P、基圆半径Rb可以推算出随动轴理论行程L，之间的关系如公式（2）所示。因此这里在实验时主轴转角取0.1弧度，基圆半径68mm，对应的随动轴位移量L距离为6.8229mm。用这些参数做为已知理论参数，在上位机中进行置数，而测头的实际位置A点与理论值有偏差，进行实验来对比加入随动控制器后的作用影响。

L=Rb×tanθ（2）

在上位机软件中置入主动轴所要转动的角度以及随动轴需要移动的行程后，驱动测量机运行，通过下位机将测头的示值进行采样导出保存，便可得到整个运行过程中测头示值的变化情况。准备好实验后进行了两组对比实验，如图5所示，第一组是系统未进行随动控制时测头的示值变化，第二组是加入随动控制后测头示值变化，图中的纵坐标代表测头的压入量，负数代表测头速度超前被测工件的转动速度，即随动轴运动速度快，正数代表测头速度落后于被测工件的转动速度，即随动轴运动速度过慢;横坐标代表测量过程中采样的点数，即运行过程中各个点的测头变化情况。

由实验结果可知，未加入随动控制时，随着测量的进行，测头示值不断减小，最终超过了-120um，即随动轴运行速度比主轴运动速度快，导致测头逐渐脱离工件表面，而使得测量结果越来越偏大;而同样的位置，在加入随动控制后，测头示值由0减小到-15um后，逐渐增加，增加到3um后保持稳定，表示加入随动控制后对存在的误差不断修正补偿，使得测头误差在增大到-15um后逐渐调节到了3um左右，测头压入量的变化范围没有超过20um，在测量过程中，对测头的压入量起到明显的补偿作用，最终使得测头的压入量变化非常小，所得到的测量结果误差也相对非常小。

4  结论

本文设计的随动控制系统可以通过测头的实际示值来调整测头的压入量，使测量机测量磨损严重或者齿面参数未知的齿轮时，可以通过测头的实际数据来实时调整随动轴带动测头运动，从而保证测头压入量始终保持在允许范围内。通过上机实验验证发现，当被测齿轮的参数不准确时，通过加入随动控制电路后可以有效的对随动轴进行补偿，从而使测头示值始终保持在设定范围内，对解决齿面方程未知齿轮以及齿面大误差齿轮的测量问题起到重要作用。

参考文献：

[1]王建华，劳奇成，刘波，张君安.CNC齿轮测量中心的原理、特点及关键技术[J].工具技术，1996（03）：41-43.

[2]劳奇成，尚雅层，王建华，李平.CNC齿轮测量中心的测控系统[J].西安工业学院学报，1996（03）：28-30.

[3]田远.基于随动控制的齿轮测量中心驱动卡的设计[D].

2015.

[4]贾振元，卫国强，郭东明，刘欣，张元良.测头控制跟踪驱动法在CNC齿轮测量仪中的应用[J].工具技术，1992（02）：35-37.

[5]马盼盼，王建華，杜虎兵，梁雯.基于SoC FPGA的CNC齿轮测量中心控制器设计[J].工具技术，2020，54（01）：103-106.

[6]曲立国.基于FPGA的智能PID控制器的研究与开发[D].安徽理工大学，2008.

[7]章魁.嵌入式智能PID控制器的研究与开发[D].安徽理工大学，2007.

[8]李垂君.基于FPGA的PID控制器研究与实现[D].大连理工大学，2008.