交通监控场景下相机标定与车辆速度测量研究(1)

韩强

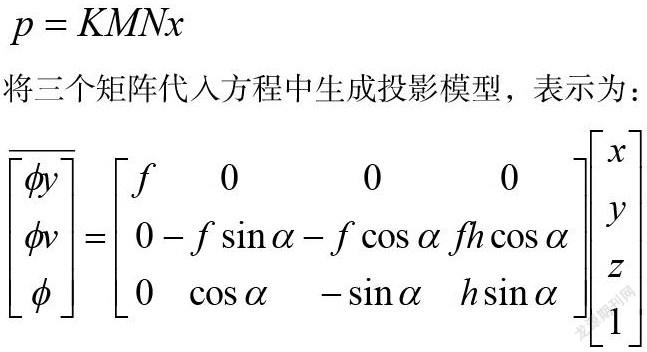
摘要：根据实际交通监控场景下的监控图像拍摄情况与行车速度测量要求，分别基于2D-3D映射关系进行目标车辆位置、运动轨迹的跟踪监测，完成道路延伸方向上车辆消失点与标志线的检测，配合车辆速度测量算法判断车辆是否超速，满足实际工程应用要求。

关键词：交通监控;相机标定;速度测量

引言

当前城市道路、高速公路等不同交通场景下已实现智能监管系统的全覆盖，依托视频图像处理、“互联网+”等手段的融合提供技术支持，适应复杂气候与路况条件下的交通监控需求。鉴于无人值守模式的推广对于监控系统的应用性能提出更高要求，研究不同场景下的自动标定及行车速度检测方案具有重要现实意义。

1基于城市道路的相机标定模型建立

1.1相机空间模型

以城市道路交通场景为例，将用于交通监控的云台相机近似为针孔模型，拟将观测路面假定为连续光滑平面，使观测主点恰好位于图像中心，以光轴延伸方向为基准作垂线定义为成像平面，并完成相关参数的设置，生成相机的空间模型[1]。将相机位置定义为原点on，建立相机坐标系xnynzn（其中xn、yn分别对应图像的行、列，zn平行于主轴），已知焦距为f，相机与路平面的间距为h，俯仰角、偏转角分别为α、β，自旋角可忽略不计，且世界坐标系为xyz（其原点o为on在路平面上的投影）。根据上述两个坐标系的空间位置关系可知，仅需将xn沿逆时针方向旋转一定角度后，沿z轴方向作大小为h的平移，即可完成坐标轴的变换，其中旋转角度为α+π/2。

在建立两个坐标系、明确变换关系的基础上，可将空间坐标系、图像坐标系中某一坐标点的齐次坐标分别表示为x=[x，y，z，1]T和p=[φu，φv，φ]T（φ≠0），则对由空间坐标到图像坐标的投影关系进行描述，将内参数、旋转、平移矩阵分别表示为K、M、N，可建立方程式：

将三个矩阵代入方程中生成投影模型，表示为：

1.2相机标定模型

在建立相机投影模型的基础上，通过分别求解出α、β、h等参数获得具体数值，但在实际交通监控场景下云台相机的内参数处于动态调整状态，难以获取到固定、准确的测量结果，因此还需引入几何表示方法进行具体数量值的求解，建立相机标定模型[2]。结合道路交通与路面实际情况，假设在路平面上存在某一点位（x，y，0），基于空间坐标、图像坐标的投影模型进行公式推理，即：

根据云台相机的自动标定特征，可将灭点的指代含义延伸至道路水平方向和垂直方向两个维度，但受实际道路交通场景下视角的局限，其中垂直方向的灭点不符合条件，仅选取道路水平方向灭点进行研究，将该点位的坐标定义为（u0，v0），将y轴与路面水平方向的夹角定义为γ，根据世界坐标系中某一坐标点的齐次坐标建立方法，将路面水平方向中某一点位的齐次坐标设为x0=[-tanγ 1 0 0]T。已知灭点是该点在图像空间中形成的投影，为便于计算将焦距设为固定值，由此可将α、γ分别表示为：

在确定灭点的基础上，结合实际道路交通监控场景下的信息需求，还需建立道路虚线、道路宽度等参数条件，保证相机标定参数的完整性。将道路虚线长度设为l，端点的物理坐标为（xb，yb）、像素坐标为（xf，yf）;将道路宽度设为p，像素长度q即道路宽度与图像坐标系截距。根据上述等式建立过程进行道路虚线物理参数模型的建立，观察其物理纵坐标与横坐标可知，二者并无直接关联性，因此可确定对于城市道路中任一点位沿道路延伸的水平方向存在一平行虚线l，存在下列等式关系：

结合不同参数之间的等式关系进行各参数间数理关系的分析，建立以下方程式：

由此确立關于焦距的四次方程式，由于在实际应用场景中相机焦距大于零，因此该方程式可能存在两个正根解，并基于一定约束条件进行焦距唯一值的判定，完成焦距数值的求解，进而获取其他标定参数，生成二维平面与三维立体转换的投影/逆投影模型。

2车辆速度测量实验设计及结果

2.1速度测量模型建立

在确立相机标定模型的基础上，可在交通监控系统中将获取到的监控图像经由相机标定处理，获取二维图像在世界坐标系平面中的映射结果。在实际道路交通中行车速度测试环节，除需精确获取相机标定参数外，还应参考不同车辆在路面中的实际运动轨迹，对此还需结合高速公路实际场景进行速度模型的建构：（1）假设高速公路场景下道路保持平坦，不受地形起伏及障碍物等影响，在此情况下满足世界坐标系下的平面要求;（2）在高速公路交通监控过程中，需以帧为单位记录车辆运行轨迹，相邻帧之间的车辆运行轨迹通常具有一定的线性变化规律，因此本文建立的速度模型对于直线、非直线移动轨迹均应具备良好适用价值;（3）假设高速公路监控系统中，相机在拍摄画面时相邻帧的时间间隔均保持一致，便于在定位车辆所处具体坐标点位的基础上，利用时间间隔完成行车速度的准确计算。

在车辆速度测量模型设计上，引入YOLO算法获取图像检测框长、宽、底边中点等参数，模拟路面真实行车速度，以视频流为基准逐帧进行目标车辆的定位，将当前帧对应的检测框底边中点设为ui（t）、前一帧坐标为ui（t-Δt）、时间间隔为Δt、轨迹点为i，则建立向量关系式：

结合相机标定模型将图像坐标系映射至对应的世界坐标系中，完成车辆运动轨迹的真实距离计算，则车辆速度公式表示为：

2.2实验结果分析

将上述模型分别应用于某城市主干路、高速公路的交通监控情境进行分析，运用Visual Studio2015平台进行实验测试，其中两不同交通场景对应的视频像素分别为1920×1080和1280×720。

观察相机标定实验结果可知，城市主干路的标定误差均值为0.76%，高速公路的标定误差均值为1.56%，高速公路的相机标定误差相对更大。针对造成误差的原因进行分析：一方面，受城市主干道路的通行高度限制，通常相机安装高度偏低，因此相机获取监控图像的清晰度相对较高，而高速公路的相机安装高度较高，因图像清晰度引发测量结果的误差;另一方面，现有交通场景下城市主干道的相机像素相对偏高，导致在实际验证环节存在一定误差。将实际误差结果进行比较可知，标定误差值控制在允许范围内，符合实际监控与检测精度要求，可为行车速度测量提供支持。

观察行车速度测量结果，在该实验中共设有A、B、C三个车道，其中A车道的算法计算结果为63.3km/h，实际车辆行驶速度为60km/h，测量结果误差控制在+5.3%;B车道的算法计算结果为62.6km/h，实际行车速度为60km/h，测量结果误差为+4.3%;C车道的算法计算结果为57.3km/h，实际行车速度为60km/h，测量结果误差为-4.5%。总体来看，车辆速度测量误差控制在6%以内，符合测量精度要求。

结论：通过结合城市主干路、高速公路两种不同监控场景进行相机标定结果与行车速度测量情况的比较分析可知，运用本文建立的算法模型可将测量误差分别控制在2%和6%以内，能够满足实际交通监控场景要求，但仍需对车辆运动轨迹进行算法优化，提高测量结果精度。

参考文献：

[1]刘金清，陈存弟.基于DSP的车道偏离检测与车辆前向车距检测[J].计算机系统应用，2020，（03）：9.

[2]李震霄，孙伟，刘明明，等.交通监控场景中的车辆检测与跟踪算法研究[J].计算机工程与应用，2021，（08）：9.