轮胎动态半径的计算及其对燃油经济性和动力性的影响

杨泽华

摘要

在一般车辆纵向动力学和能量分析的仿真计算中，轮胎动态半径是1个非常重要的参数，但在实际操作中，该参数准确的数值较难获取。探讨了欧洲轮胎与轮辋技术组织（ETRTO）推荐方法、AVL CRUISE软件计算方法、动态试验方法等5种轮胎动态半径的计算方法。基于AVL CRUISE软件仿真计算，获得不同轮胎动态半径下的车辆在新欧洲行驶循环（NEDC）工况下的燃油经济性及动力性仿真计算结果，并对仿真结果进行了理论分析。仿真结果及理论分析显示，轮胎动态半径对车辆燃油经济性和动力性有较大影响。轮胎动态半径的参数取值须得到重视。为获得高精度的仿真计算结果，推荐使用轮胎动态半径随车速的曲线代替单一动态半径值进行计算。

關键词

轮胎动态半径;仿真计算;燃油经济性;动力性

①为了符合本行业习惯，本文仍沿用部分非法定计量单位——编注。

0 前言

轮胎特性具有明显的非线性特征，且轮胎与路面相互作用关系非常复杂，这些因素使其具有复杂的力学特性，并会对车辆动力学产生非常重要的影响[1-2]。尽管一般车辆纵向动力学和能量仿真分析对轮胎特性参数的要求相对较低，但是轮胎是将车辆动力总成系统的旋转运动变为平动的重要部件，其中轮胎动态半径是1个非常重要的参数，轮胎动态半径的改变会对车辆燃油经济性和动力性产生影响。因此，仿真计算中轮胎的动态半径数值的设定尤为重要。动态半径受到温度、压力、车速，以及轮胎结构等多种因素的影响，技术人员较难获取相应的参数，其测试过程较为复杂，且耗资巨大。

本文基于相关文献的计算方法，分别对车型为桑塔纳2000（Santana  2000），轮胎型号为 195/60 R14 85H的轮胎动态半径进行了计算，并对各计算方法特点进行了总结。本文推荐动态半径表征为车速的函数，在实际操作过程中可以根据具体情况选择合适的方法;本文还利用计算机仿真分析了轮胎动态半径对整车燃油经济性及动力性的影响。结果表明，该数值对精确的燃油耗仿真计算结果有明显影响。在仿真计算时，该数值参数的取值需要引起技术人员的重视。

1 轮胎动态半径计算方法探讨

在对轮胎动态半径计算方法进行探讨之前，本文先对轮胎规格作一些说明。以Santana 2000使用的轮胎为例，其型号为195/60 R14 85H。该轮胎型号中的“195”表示轮胎截面宽度为195 mm;“60”表示轮胎截面高度与轮胎宽度的比值为60%，即当轮胎宽度为195 mm时轮胎截面高度为117 mm;“R14”代表轮毂的直径为14 in①（1 in等于25.4 mm）;“85”表示负荷指数，即规定的车速和气压条件下的最大装载质量，此轮胎所能承受的最大载质量为515 kg;“H”是车速的等级标志，表示该轮胎的最高车速允许达到210 km/h。如果技术人员已知了轮胎的规格参数，一般可以通过查阅相关工业标准得到轮胎的动态半径数值。

在理论上，轮胎动态半径可以用车轮转动圈数与实际车轮滚动距离之间的关系来计算[3]，如式（1）所示。

r=S2πnw（1）

式中，nw为车轮转动的圈数;S为转动nw圈时车轮滚动的距离，单位mm。

下文列举5种轮胎动态半径的计算方法，包括试验和理论近似计算方法。

1.1 欧洲轮胎与轮辋技术组织（ETRTO）推荐方法

根据ETRTO推荐的计算公式，图 1示出了Santana 2000所使用的轮胎型号为195/60 R14 85H的动态半径随车速变化的曲线图。采用该计算方法时，在车速为120 km/h的情况下，轮胎动态半径和轮胎静态半径相差很小，约为4 mm，动态半径与车速呈线性关系。

1.2 AVL CRUISE软件计算方法

AVL CRUISE软件中自带有轮胎半径计算器，技术人员只要输入轮胎的宽度、宽径比、轮圈直径等参数，就可以计算出轮胎的周长、静态半径和动态半径。该软件的计算器内核是1个JavaScript程序。动态半径计算方法与ETRTO推荐的方法基本一致，但该方法仅能计算1个状态下的动态半径。轮胎的静态半径为轮毂半径与0.78倍的轮胎截面高度之和。由此，技术人员可计算出Santana 2000轮胎的静态半径为269 mm。显然这是1个经验公式。

技术人员将Santana 2000轮胎的参数填入AVL CRUISE软件自带计算器中，计算结果显示其动态半径数值为286 mm（图2）。该结果与ETRTO推荐的计算方法所得结果基本一致。在规定气压、满载状态、车速为60 km/h时，轮胎对应的动态半径为286 mm。

1.3 动态试验方法

李伟华[4]在论文《汽车行驶特性仿真与动力总成匹配优化》中提到，曾对Santana 2000型轿车做过轮胎的动态试验。他认为，轮胎动态半径主要取决于选用的轮胎型号及使用情况，在轮胎气压及承受载荷一定的情况下，可视为关于车速的函数。对于Santana 2000型轿车，轮胎动态半径的计算公式如式（2）所示。

r=1 000×（0.288+3×10-5×3.6va+6.11×10-7×3.62va2）（2）

式中，va为车速，单位m/s。

轮胎动态半径随着车速的提高而逐渐增大，图3示出了轮胎动态半径随车速变化的曲线图。由图3可以看出，当轮胎静态半径为288 mm、车速为120 km/h时，动态半径略高于300 mm。试验获得的动态半径数值较前几种方法得到的结果略偏大，这可能是由于试验本身存在误差，且轮胎的承受载荷和温度条件也有差异的缘故。

1.4 K UWE和N LARS的计算方法

K UWE和N LARS在其著作《Automotive Control Systems》中也推导了1种动态半径计算方法[5]，该计算公式如式（3）所示。

r=ro·sin（arccos（rsro））arccos（rsro）（3）

式中，ro为轮胎自由半径，单位mm，其值为轮毂半径与轮胎截面高度之和;rs为轮胎静态半径，单位mm。

根据Santana 2000轮胎的规格参数，可计算出ro为295 mm。轮胎静态半径的计算公式，如式（4）所示。

rs=ro-Fzkt（4）

式中，Fz表示轮胎所受垂直方向的反力，单位N;kt表示轮胎的刚度，单位N/mm。由于轮胎垂向刚度与轮胎的气压、所受载荷，以及车速有直接关系，且较为复杂，通常这2个变量较难获取。

根据图2求出Santana 2000轮胎的静态半径为269 mm，可以求得应用K UWE方法时的轮胎动态半径为286 mm。若使用李伟华在试验方法中提到的静态半径288 mm，则计算出的动态半径为293 mm。基于不同的静态半径，计算出的动态半径差别较大。

1.5 发动机转速、车速、速比的推算方法

技术人员根据车辆动力总成传动系统相关理论，可以推导出车轮转速，如式（5）所示。

ωw=2πn60igif（5）

式中，n为发动机转速，单位r/min;ig为变速器速比;if为主减速器速比。

如果该状态下的车速已知，则可以计算出轮胎的动态半径，如式（6）所示。

r=1 000 va/ωw（6）

式中，va为车速，单位m/s;ωw为车轮转速，单位 rad/s。

在应用式（6）时，技术人员应使车辆处于稳态，控制发动机转速以保持车速恒定，且严格标定发动机转速、车速，以及档位信号。在实际操作过程中，发动机的电子控制单元（ECU）可以给出精确的数值。 由于ECU内部的车速是由传感器基于变速箱输出轴标定或者轮速传感器标定推算出来的，其数值与动态半径相关，将其值直接用于动态半径计算并不准确。因此，车速数值建议从转毂测试设备中读取。

图4示出了某车辆在不同固定点车速下轮胎动态半径随车速的变化曲线。试验结果显示，在各固定点车速下，轮胎的动态半径在275～290 mm之间，数值范围可以作为仿真计算输入参考。

表1示出了不同轮胎动态半径计算方法的特点。通过对各计算结果进行对比，动态半径表述为车速的函数较为合理。如果需要获得高精度的仿真计算结果，本文推荐使用动态半径随车速的曲线代替单一动态半径值。

2 轮胎动态半径对车辆燃油经济性和动力性的影响

以AVL CRUISE自带的前驱手动变速器车辆为基础，技术人员通过改变轮胎的动态半径，分别计算出新欧洲行驶循环（NEDC）工况下燃油消耗、最高车速、最大爬坡度，以及0～100 km/h的加速时间。该车型为AVL CRUISE自带的前驱手动变速车辆模型。假设地面附着系数最大为0.8，以原车轮胎滚动半径312 mm作为基准，且计算过程已考虑了由于轮胎半径减小造成的重心垂直方向上位置的差异。仿真计算结果如表2所示。

由表2可以看出，在不考虑改变轮胎滚动半径后引起的车辆行驶滚动阻力的变化和车重变化时，随着轮胎动态半径的增大，车辆在NEDC工况下的燃油耗会有所降低。图5示出了轮胎动态半径对车辆燃油经济性和动力性的影响。

式（7）示出了车速与发动机转速之间的对应关系。

va=2πrn60ig if÷1 000（7）

式中，r为轮胎动态半径，单位mm;n为发动机转速，单位r/min;ig为变速器速比;if为主减速器速比。

式（8）示出了驱动力与发动机扭矩之间的对应关系。

Ft（va）=1 000×Te ig ifηr（8）

式中，Te为发动机扭矩，单位N·m;ig为变速器速比;if为主减速器速比;η为传动系传动效率;r为轮胎动态半径。

在车辆匀速状态时，发动机的需求功率如式（9）所示。

P=（f0+f1va+f2va2）va/η（9）

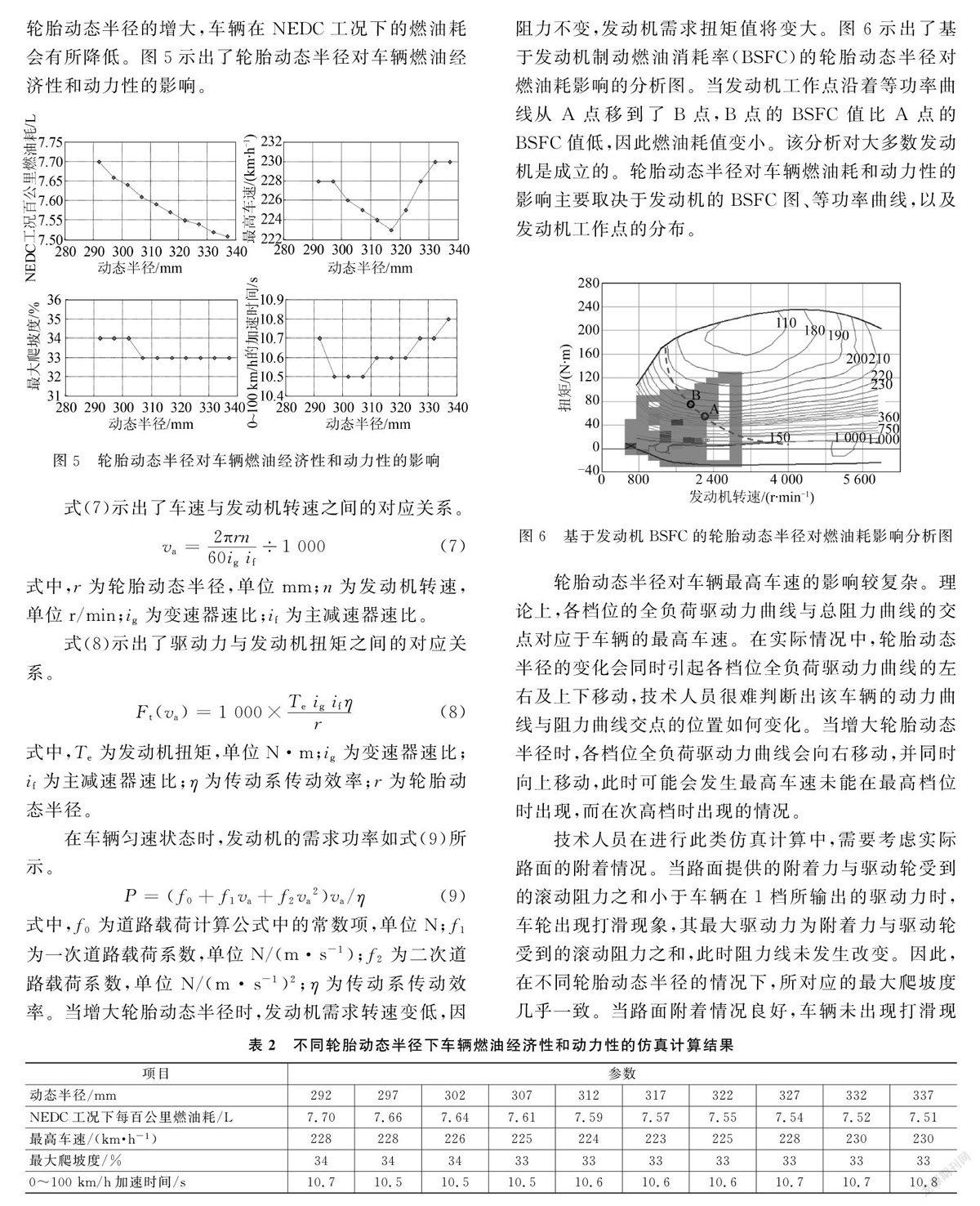
式中，f0为道路载荷计算公式中的常数项，单位N;f1为一次道路载荷系数，单位N/（m·s-1）;f2为二次道路载荷系数，单位N/（m·s-1）2;η为传动系传动效率。当增大轮胎动态半径时，发动机需求转速变低，因阻力不变，发动机需求扭矩值将变大。图6示出了基于发动机制动燃油消耗率（BSFC）的轮胎动态半径对燃油耗影响的分析图。当发动机工作点沿着等功率曲线从A点移到了B点，B点的BSFC值比A点的BSFC值低，因此燃油耗值变小。该分析对大多数发动机是成立的。轮胎动态半径对车辆燃油耗和动力性的影响主要取决于发动机的BSFC图、等功率曲线，以及发动机工作点的分布。

轮胎动态半径对车辆最高车速的影响较复杂。理论上，各档位的全负荷驱动力曲线与总阻力曲线的交点对应于车辆的最高车速。在实际情况中，轮胎动态半径的变化会同时引起各档位全负荷驱动力曲线的左右及上下移动，技术人员很难判断出该车辆的动力曲线与阻力曲线交点的位置如何变化。当增大轮胎动态半径时，各档位全负荷驱动力曲线会向右移动，并同时向上移动，此时可能会发生最高车速未能在最高档位时出现，而在次高档时出现的情况。

技术人员在进行此类仿真计算中，需要考虑实际路面的附着情况。当路面提供的附着力与驱动轮受到的滚动阻力之和小于车辆在1档所输出的驱动力时，车轮出现打滑现象，其最大驱动力为附着力与驱动轮受到的滚动阻力之和，此时阻力线未发生改变。因此，在不同轮胎动态半径的情况下，所对应的最大爬坡度几乎一致。当路面附着情况良好，车辆未出现打滑现象时，增大轮胎动态半径，其驱动力将降低，此时车速较低，阻力变化不大，用于爬坡的剩余驱动力会相应变小，因此车辆的最大爬坡度将变小。

轮胎动态半径对车辆0～100 km/h加速时间的 影响也较为复杂。轮胎动态半径的变化，会引起各档位在全负荷时所对应的加速度与车速的曲线产生左右或上下移动。根据车辆在各档全负荷下的加速度与车速等参数，技术人员得到加速度倒数曲线与速度的关系图，并用加速度倒数对速度求积分，可以得到车辆最短的0～100 km/h加速时间。由于车辆的加速时间较短，增大轮胎半径容易出现驱动力变小、加速度变小、加速性能变差的现象。

3 结论

在车辆纵向动力学和能量分析仿真计算中，轮胎动态半径是1个非常关键的参数。该参数对在NEDC工况下的车辆燃油耗及动力性会产生一定的影响，特别是对车辆燃油耗的仿真计算影响较大。技术人员在相关的仿真计算中应足够重视该仿真计算。但在实际操作中，该参数精准的数值又较难获取。本文提供了5种轮胎动态半径的计算方法，技术人员可以根据实际情况选取合适的计算方法。本文建议现场测量1个静态半径作为参考数值。如对仿真计算结果精度要求较高，则推荐使用动态半径随车速的曲线代替单一动态半径值。在通常情况下，增大轮胎半径可以使NEDC工况下的燃油经济性提高。然而，轮胎半径的变化对车辆动力性的影响较为复杂，在车辆动力总成匹配中等效于改变传动系速比。在一般情况下，增大轮胎半径可能会导致车辆加速性能变差。

参考文献

[1]喻凡，林逸. 汽车系统动力学[M]. 北京：机械工业出版社，2005.

[2]HENNING W. Longitudinal dynamics of vehicles[M]. 北京：机械工业出版社，2009.

[3]余志生. 汽车理论[M]. 北京：机械工业出版社，2000.

[4]李伟华. 汽车行駛特性仿真与动力总成匹配优化[D].上海：上海交通大学， 2000.

[5]UWE K，LARS N. Automotive control systems[M]. Germany：Springer Verlag，2004.