“导生制共同学习”的教学实践与思考

摘    要：“导生制共同学习”是聚焦群体学习和社会文化场景学习的一种教学形式，苏州市平江中学校在多年实践探索的基础上，形成了“243”课堂组织架构。下面以“图形的相似”复习课教学为例，谈一谈本人在开展“导生制共同学习”教学实践中的体会与思考。

关键词：初中数学;导生制共同学习;“243”课堂架构

一、关于“243”课堂组织架构

“导生制共同学习”是“共同学习”与“导生制”融合的产物，这种教学形式的价值意义在于学习过程中每个人都有不同的角色互换，每个人都有成为某个领域“导生”的机会，成为同伴的“小老师”，在共同学习中起到组织、引领和服务的作用，这对于培养团队精神和促进他们合作能力的发展十分有利。

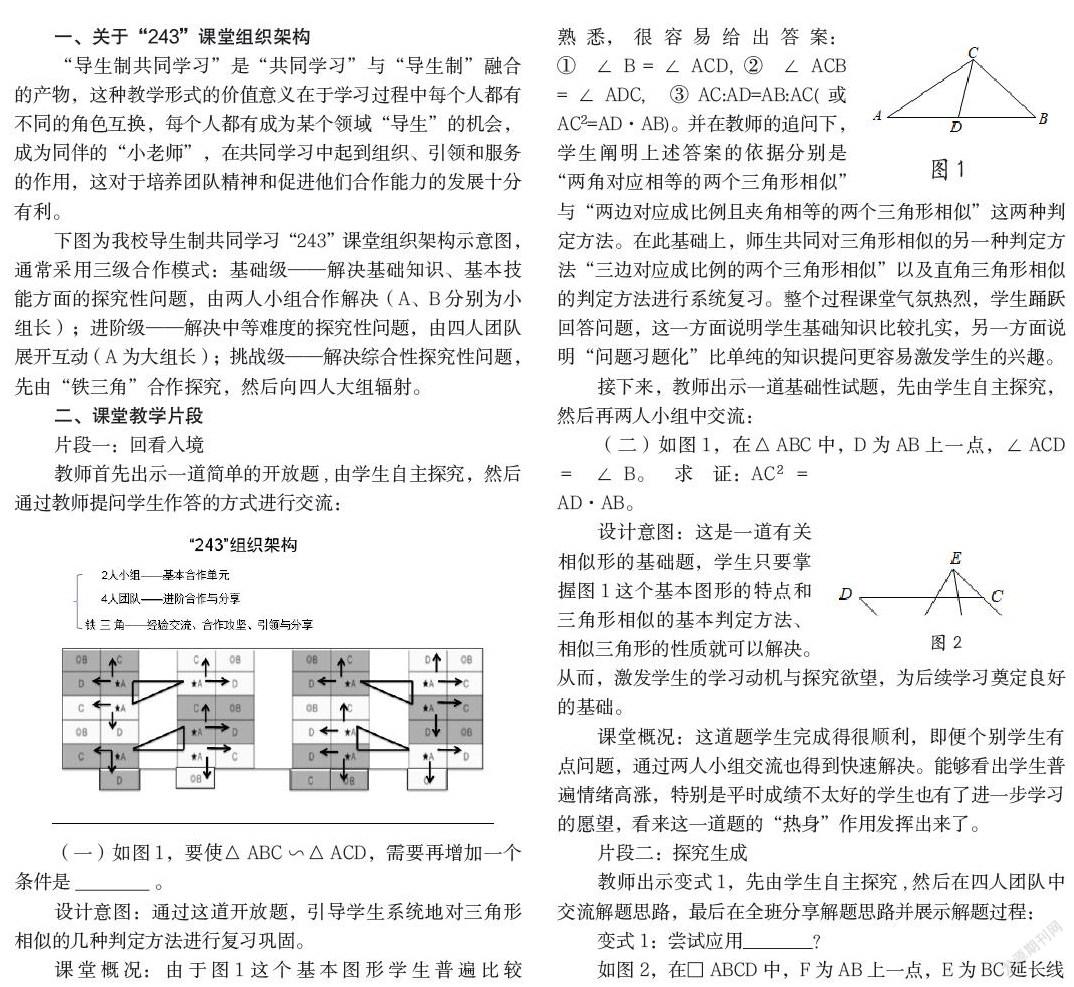
下图为我校导生制共同学习“243”课堂组织架构示意图，通常采用三级合作模式：基础级——解决基础知识、基本技能方面的探究性问题，由两人小组合作解决（A、B分别为小组长）;进阶级——解决中等难度的探究性问题，由四人团队展开互动（A为大组长）;挑战级——解决综合性探究性问题，先由“铁三角”合作探究，然后向四人大组辐射。

二、课堂教学片段

片段一：回看入境

教师首先出示一道简单的开放题，由学生自主探究，然后通过教师提问学生作答的方式进行交流：

（一）如图1，要使△ABC∽△ACD，需要再增加一个条件是。

设计意图：通过这道开放题，引导学生系统地对三角形相似的几种判定方法进行复习巩固。

课堂概况：由于图1这个基本图形学生普遍比较熟悉，很容易给出答案：①∠B =∠ACD，②∠ACB =∠ADC， ③AC：AD=AB：AC（或AC2=AD·AB）。并在教师的追问下，学生阐明上述答案的依据分别是“两角对应相等的两个三角形相似”与“两边对应成比例且夹角相等的两个三角形相似”这两种判定方法。在此基础上，师生共同对三角形相似的另一种判定方法“三边对应成比例的两个三角形相似”以及直角三角形相似的判定方法进行系统复习。整个过程课堂气氛热烈，学生踊跃回答问题，这一方面说明学生基础知识比较扎实，另一方面说明“问题习题化”比单纯的知识提问更容易激发学生的兴趣。

接下来，教师出示一道基础性试题，先由学生自主探究，然后再两人小组中交流：

（二）如图1，在△ABC中，D为AB上一点，∠ACD=∠B。求证：AC2=AD·AB。

设计意图：这是一道有关相似形的基础题，学生只要掌握图1这个基本图形的特点和三角形相似的基本判定方法、相似三角形的性质就可以解决。从而，激发学生的学习动机与探究欲望，为后续学习奠定良好的基础。

课堂概况：这道题学生完成得很顺利，即便个别学生有点问题，通过两人小组交流也得到快速解决。能够看出学生普遍情绪高涨，特别是平时成绩不太好的学生也有了进一步学习的愿望，看来这一道题的“热身”作用发挥出来了。

片段二：探究生成

教师出示变式1，先由学生自主探究，然后在四人团队中交流解题思路，最后在全班分享解题思路并展示解题过程：

变式1：尝试应用？

如图2，在□ ABCD中，F为AB上一点，E为BC延长线上一点，∠AEF=∠D。若AE=6，BF=5，求CD的长。

设计意图：这是一道背景较为复杂的综合题，巧妙地把形如图1结构的基本图形嵌入平行四边形中，这无疑增加了试题的思维含量，给学生分析和解决问题带来一定难度。希望在自主探究的基础上，通过四人团队的合作交流，能够紧扣题目条件，找到解决问题的突破口，把复杂问题转化为“回看入境”试题（二）这样的简单问题来解决。

课堂概况：能够看出，这道题对一些基础较好、思维能力较强的学生来说，思维难度不算太大。根据条件“∠AEF=∠D”和“平行四边形对角相等”的性质，立得“∠AEF=∠B”，从而证得△AEF∽△ABE，这样问题就迎刃而解了。这些学生形成解题思路后，另有一些学生在他们的启发下也有了思路，之后又通过四人团队的交流，全班学生都顺利完成解答过程。整个探究过程对学生而言，不仅收获了解题方法，更重要的是随着探究活动的深入，学生学习渐入佳境，思维也逐步得到拓展和提升。

片段三：拓展提升

教师出示变式2，先由学生自主探究，然后在四人团队中交流解题思路。如果四人团队最终无法形成解题思路，就要通过“铁三角”攻坚克难，然后再把所形成解题思路向各自的四人团队进行辐射，实现成果共享。

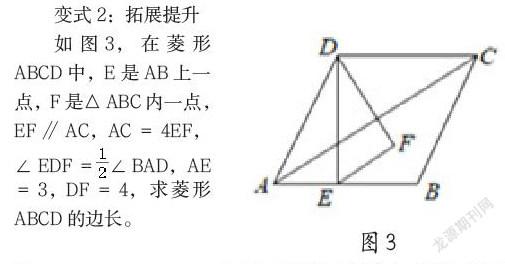
变式2：拓展提升

如图3，在菱形ABCD中，E是AB上一点，F是△ABC内一点，EF∥AC，AC=4EF，∠EDF=∠BAD，AE=3，DF=4，求菱形ABCD的边长。

设计意图：此题是一道以菱形为背景、以三角形相似的判定方法及相似三角形的性质为工具的综合题。解决此题的关键在于通过构造□AEGC，得到形如图1结构的基本图形，并最终形成解题思路。

课堂概况：这道题由于题目的条件较多且比较散乱，思维难度大，学生不容易发现解题线索，很明显每个四人团队的探究活动都遇到巨大阻力，无法正常推进下去。于是，教师提议启动“铁三角”，并提示学生注意把握这道题与上述题目在本质上的关联，并以此为突破口，寻求解题途径。在各个“铁三角”的探究过程中，教师参与其中给予指导和帮助，最终各个“铁三角”相继突破解题瓶颈，形成解题思路。之后把探究结果分享到四人团队中，各自完成解答过程。最后教师指定学生在全班交流解题过程，并及时进行点评。

在这道题的探究过程中，虽然花费了相当多的时间和精力，但对学生而言，会产生登高望远的快感，创新灵感得到进一步激发，思维得以提高。同时，通过探究活动的深入开展，既培養了学生克服困难、勇于探索的意志品质，又培养了团队协作能力，形成共同学习的良好氛围。

解：如图4，延长DC、EF，交于点G，

∵四边形ABCD是菱形，∴AB∥DC，∠BAC=∠BAD，

∵AC∥EF，∴四边形AEGC为平行四边形，

∴AC=EG，CG=AE，∠EAC=∠G，

∵∠EDF=∠BAD，∴∠EDF=∠BAC，

∴∠EDF=∠G，

又∵∠DEF=∠GED，∴△EDF∽△EGD，∴=，

∴DE 2=EF·EG，

又∵EG=AC=4EF，∴DE 2=4EF 2，

∴DE=2EF，

又∵=，∴DG=2DF=2×4=8，

∴DC=DG﹣CG=8﹣3=5.即菱形ABCD的边长为5。

三、几点思考

（一）精心选择活动素材和设计学习活动是开展“导生制共同学习”的前提。 实践表明，共同学习必须建立在“任务驱动”的前提下。在新课学习时，教师可以选择具有挑战性的数学问题或实际生产生活中的热点问题等，构建起学生探究、发现、生成新知的思维场域，使学生在获取知识的同时获得基本的数学活动经验;在习题课或复习课中，可以通过设计以能力立意的问题串或变式题等，构建起学生思维品质形成和思维进阶的思维场域，使得不同层次的学生都能够在探究活动中产生成就感。

（二）独立思考、自主探究是开展“导生制共同学习” 的基础。 在共同学习的过程中，切不能离开学生的独立思考、自主探究。否则，“导生制共同学习”就失去了基础，共同学习将不会深入，或浮于表面、流于形式，或半途而废、无功而返。因而，教学时，面对问题和挑战，教师不宜过早介入，共同学习也要择机而行，让学习真正发生，促进学生深度学习。

（三）教师的有效调控是开展“导生制共同学习”的关键。一是要关注“导生”在组织、引导本组成员开展探究活动时的表现，是否在任务驱动下进行合理分工，是否有效调动每个成员的主观能动性，推动探究活动有序进行;二是要关注各小组成员的参与程度，清楚不同层次学生的表现，注意学生的话语走向，对偏离主题的现象及时点明并加以引导;三是关注各小组问题探究的进程，掌握各小组的学习困惑，对思维碰撞比较激烈并且一时无法形成共识的小组及时给予指导和帮助，对各小组存在的共性问题则需要集中释疑破难。

（四）注重评价跟进是开展“导生制共同学习”的重要手段。由于“导生制共同学习”的基本形式是学习共同体，因而其课堂评价不仅要针对学生个体，更要指向团队整体表现，以团队在学习过程中的参与度和参与质量为主要标准，采取评价目标多元、评价方式多样的评价思路。

参考文献：

[1] 邓大一，王恒昌.  共同学习：社会协商本质下的学习认知过程——平江中学“导生制”的哲学意蕴. 華人时刊 · 校长. 2018（12）