基于主从博弈的负荷聚合商日前市场最优定价策略
孙伟卿,刘晓楠,向 威,李宏仲
(1. 上海理工大学机械工程学院,上海市200093;2. 上海申能新动力储能研发有限公司,上海市201419;3. 上海电力大学电气工程学院,上海市200090)
0 引言
随着可再生能源和用户侧可调负荷的大规模并网[1],以及多种能源互联[2]和现货市场的构建[3],不同形式能源在生产和消费环节的耦合性越来越强。需求响应能够反映市场竞争和需求弹性发展[4],为用户侧资源参与电力市场和实现“源-荷”双向互动提供新局面[5]。在此背景下,负荷聚合商(load aggregator,LA)作为聚合大量可调节负荷资源的新兴市场主体得以迅速发展[6]。然而,可调负荷资源具有多类型、多规模、布局分散且响应不确定的特征[7],且用户参与需求响应存在偏好[8],制约了需求响应参与市场的可靠性和竞争力。另一方面,LA可影响用户响应定价策略的制定,进而影响其参与市场的响应电量与收益。
目前国内外关于LA 的研究主要关注其运行控制和市场竞争策略。文献[9]从整合需求侧资源角度,提出了LA 商业化模式的实施方法和途径。在此基础上,文献[10-11]研究了需求侧资源的不确定性对LA 自身投标决策的影响,建立了聚合商的最优竞价策略。文献[12]基于信息缺口决策理论,建立了采用数据驱动的聚合商在非合作电力市场中的投标策略。文献[13-14]考虑市场中电价风险及分布式资源响应的不确定性,建立了聚合商的风险规避优化报价策略。文献[15]基于协整理论,构建考虑误差修正的直购电价与发电成本的关系模型,实现供需两侧利益最大化的双边博弈。以上研究均为实现LA 参与下的系统整体最优[16-17],对LA 与其他市场交易主体的报价策略进行了优化,但未计及LA 在资源调控过程中对用户响应定价策略的优化。
另一方面,在实际情况中,用户侧资源响应的不确定性和用户的响应偏好,使其参与电网调节的作用难以充分发挥。文献[18-21]对灵活性负荷进行分类,针对不同负荷资源的用电特性和响应特性,以负荷自身为主体从系统优化配置和调度运行的角度进行讨论,未考虑用户行为的影响。文献[22-23]采用灵活性参数描述用户偏好,引入满意度评价函数分析用户效用,建立不同时间尺度的市场电价策略。本文将用户侧可调节电力负荷聚合作为广义需求 侧 资 源(generalized demand side resource,GDSR),从用户决策层面,通过考虑用户响应偏好对GDSR 进行优化控制,可有效平抑负荷曲线的波动性[24],减轻电网的调节压力。
为有效挖掘不同偏好用户的需求响应潜力并最大限度地提高LA 收益,提出一种基于价格激励的需求响应机制,以用户和LA 各自利益最大为目标构建主从博弈模型。LA 通过调整定价优化用户响应提高收益,求解模型迭代分析激励价格对用户成本和LA 收益的敏感性,获得LA 最优激励价格。采用最优定价下的控制策略,在保障用户用电满意度的前提下实现区域内负荷平抑。
1 基于需求响应的GDSR 优化控制
LA 代理用户向电网提供负荷平抑服务,在满足辖区用户用电需求的同时平抑负荷曲线。LA 通过价格激励[25]用户参与响应,用户随响应价格变化优化自身用电行为,在用电成本与满意度之间达到最优均衡[26]。用户和LA 均以自身利益最大化为目标进行博弈。LA 博弈的策略为各时段响应定价;用户博弈的策略为各时段响应电量。
1.1 基于价格激励的需求响应机制设计

若LA 未能成功平抑负荷波动,将带来系统安全风险上升和高昂的边际成本,因此,阈值以外的购买价格将降低,且价格变化与超限规模正相关。LA提供的响应曲线为Qpur,每时段响应电量Qpur,t数值上为响应前后负荷需求电量的差值。
考虑用户控制GDSR 参与响应的方式有2 种:一是用户与LA 签订合约削减或增加负荷参与响应,约定参与响应补偿价格和响应电量;二是用户参与差额响应,即LA 在电量交割时根据电量差额激励用户削减或增加负荷进行响应。同一用户不可同时参与2 种响应方式。
1)合约响应
LA 对合约用户的补偿价格采用分时电价,负荷超限时段LA 调整原补偿价格曲线,激励用户改变响应电量以实现负荷波动平抑。用电价格曲线为e=[e1,e2,…,eT],补 偿 价 格 曲 线 为 λ=[λ1,λ2,…,λT]。
2)差额响应
用户不参与响应时按照分时电价e 购电,参与响应时各时段的用电价格按照一定的价格调节比率进行调整,实际用电价格曲线为e′=[e′1,e′2,…,e′T]。用户根据用电需求选择是否响应电价调整,不参与需求响应的用户购电价格仍采用原电价曲线。
1.2 用户行为分析建模
1)合约响应用户
定义用户i 在t 时段的效用函数ui,t(QGDSR,i,t,ωi)为响应电量QGDSR,i,t及偏好系数ωi的函数,表示用户对需求响应效用的评估。偏好系数ωi用于区分不同用户响应偏好,且ωi>0。ui,t(QGDSR,i,t,ωi)可表示为:

式中:λt为t 时段合约响应的补偿价格;Qideal,i为用户i 的理想响应电量。设置QGDSR,i,t中削减响应量为正,增加响应量为负。式(4)等号右边第1 项为用户i 在t 时段的响应补偿收益;第2 项为用户i 在t 时段的响应不满意度,反映用户在成本和舒适度间的权衡。
定义T 个时段内用户效用与用户购电成本的差值为用户收益,则用户i 的收益可表示为:

式 中:Fuser,i为T 个 时 段 用 户i 的 收 益;et为t 时 段 用 户的购电价格;Quse,i,t为t 时段用户i 的计划用电量。
用户参与合约响应的GDSR 受到调用功率约束及补偿价格约束:

式 中:e′t为t 时 段 用 户 的 实 际 用 电 价 格;Quse,k,t为t 时段用户k 的原计划用电量;QGDSR,k,t为t 时段用户k 的差额响应电量;Qideal,k为用户k 的理想响应电量;ωk为用户k 的用电偏好系数。
实际用电价格e′t为关于价格调节比率的函数:

式中:φ(t)和φ(t)为电价调整比率;δ(t)为0-1 变量,取1 时用户增加负荷,取0 时用户削减负荷。
则差额响应用户的收益可表示为:
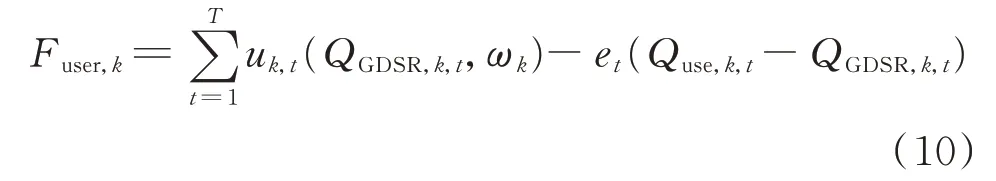
用户参与差额响应的GDSR 受到用电价格约束及可调电量限度约束:

式中:padd,t和pcut,t分别为t 时段用户可调节负荷的最大增加和削减比率。
用户集N 中所有用户在t 时段的响应电量为单个用户响应电量之和,具体可表示为:
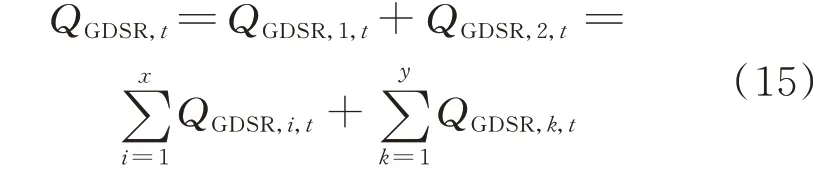
式中:QGDSR,t为用户总响应电量;QGDSR,1,t和QGDSR,2,t分别为t 时段总合约响应电量和差额响应电量,由单个用户的响应电量累加得到;x 和y 分别为参与2 种响应的用户数量。
同样可得到所有用户在t 时段的用电量为:
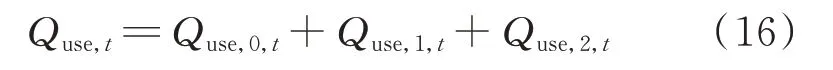
式 中:Quse,t为 用 户 总 用 电 量;Quse,0,t,Quse,1,t,Quse,2,t分别为t 时段不参与响应、参与合约响应和参与差额响应的用户用电量,其值分别为单个用户的用电量之和。
1.3 LA 行为分析建模
LA 与电网签订合同提供负荷平抑服务获取收益,通过调整补偿价格λ 和购电价格e′,激励用户参与响应,使自身利益最大化。其收益表达式为:

等号右边第1 项为LA 提供负荷平抑服务的收益;第2 项为LA 的补偿成本,具体可表示为:

等号右边第1 项为LA 对参与合约响应用户的补偿成本;第2 项为LA 对参与差额响应用户的补偿成本。LA 的收益受电网合约电量和合约价格的约束。
2 LA 最优定价的主从博弈模型
在博弈过程中,LA 首先根据与电网签订的合同,以自身收益最大为目标生成补偿价格和用电价格曲线发布给各个用户;每个用户以自身利益最大化(综合成本最小)为目标优化响应,并将负荷和响应曲线反馈给LA。该过程构成了典型的主从博弈模型,其中LA 为决策者、各个用户为跟随者。因此,根据逆向归纳法[27],首先将关于λ 和e′的LA 收益Ipro最大化,进而将调整后的λ 和e′分别代入每个用户的收益Fuser,i和Fuser,k优化QGDSR,t。
2.1 主从博弈模型
在主从博弈问题中,LA 与各个用户均以自身利益最大化为目标,属于非合作博弈。
就第m 个用户而言,最优策略满足:

2.2 最优定价策略
为获得各个用户对LA 设定价格的最佳响应,分别对2 类用户效用模型进行求解。
1)考虑给定不同时段的补偿价格λt,求用户i 的收益Fuser,i关于响应电量Q∗GDSR,i,t的一阶偏导数:

2.3 均衡解存在性分析
当每个参与者在其他参与者决策给定的条件下都使得自身利益最大时,博弈达到均衡。假设博弈中用户与LA 的策略组合为Γ={{Qm}m∈N,e′,λ},其中Qm为第m 个用户的 策略集;e′和λ 为LA 的策略集。则Γ∗为博弈均衡解的充分必要条件是:对任意参与者(用户或LA)β 的策略τβ(τβ可以为Qβ,e′或λ),均有

式中:Wβ表示β 的收益;Γ∗||τβ表示只有β 单独改变Γ∗中自身策略,其他参与者策略不变。即在均衡解Γ∗下,任一参与者均无法通过单方面改变自身策略获得更高利益。
本文的博弈问题为非合作博弈,不一定有均衡解[28],故需进行均衡解存在性分析。对合约响应用户i,博弈中λ 为已知量,其优化问题可表示为:

目标函数为关于Qi的T 元二次函数,在空间RT内处处连续且可微,且可行域封闭,因此在可行域内必定存在至少一个最小值。即在任一λ 下,用户均能找到最优响应策略,当且仅当λ 为最优补偿定价λ∗时,博弈达到均衡。
同样地,对差额响应用户k 而言,e′为已知量,在任一e′下,用户均能找到最优策略,当且仅当e′为最优用电定价e′∗时,博弈达到均衡。
LA 分别对不同响应类型用户的定价策略进行单独优化。在给定Q 的情况下,LA 的优化问题变为关于λ 和e′的T 元二次函数,且可行域封闭,因此必然存在最优策略λ∗和e′∗使得其利益最大。
3 主从博弈模型优化算法
在主从博弈中,LA 是博弈的主导者,用户根据LA 的定价策略及自身用电需求决定其响应策略。因此,LA 的定价策略为博弈策略组合Γ 最重要的变化成分,通过设计LA 的电价调整优化算法获得主从博弈模型的最优解。算法流程如图1 所示。

图1 优化算法流程图Fig.1 Flow chart of optimization algorithm
正常运行阶段,LA 发布需求响应价格信息,用户按分时电价e 购电,LA 汇总用户信息得到未来T时段总负荷曲线Q 和需求响应计划Qpur,求解自身收益Ipro,0。在此阶段,LA 未接收负荷平抑需求且定价策略不做调整,LA 调控GDSR 进行需求响应参与市场获取收益。LA 收到负荷平抑信号后判断负荷平抑需求,若max(Q)≥Q+thsd或min(Q)≤Qthsd,则LA 需调整价格曲线优化用户响应,进入LA 与用户的主从博弈过程。在负荷平抑阶段,LA 将初始收益赋值为最大收益Ipro,max,用以与调整价格时的收益对比。用户根据调整后的价格信息调整自身响应电量并计算收益,LA 根据用户反馈调整价格并计算收益Ipro,n,若Ipro,n大于Ipro,max则更新Ipro,max。当用户收益小于正常运行阶段收益时退出响应,随着电价调整参与响应的用户数量逐渐减少,直到全部退出。在此过程中,LA 更新Ipro,max并找到最优的定价策略e′max和λmax,此时GDSR 的响应量最优。最后,LA 判断自身收益决策是否参与负荷平抑响应。
4 算例分析
本文设定优化周期T 为24 h,时段间隔为1 h,LA 辖区内用户数为1 000。根据文献[28]的用户偏好特性将用户分为A,B,C 三类典型用户:A 类以满足自身用电需求为主;B 类以用电成本最小为主要目标;C 类考虑用电成本与用电方式的均衡,具有较高的价格敏感性。用户个体刚性负荷相同,每个用户的响应电量不低于自身可调负荷总量的30%,总可调GDSR 容量为34.5 MW·h。假设LA 于当日00:00 收到负荷平抑控制需求,峰时控制阈值为38 MW·h,谷时控制阈值为28 MW·h。峰平谷时段划分如附录A 表A1 所示,相关参数设置如附录A表A2 所示。
4.1 电价调整与收益分析
图2(a)中显示了LA 未收到负荷平抑需求时的负荷曲线,3 类用户在正常运行阶段的响应电量如图2(b)所 示。 此 时3 类 用 户 的 成 本 分 别 为77.384 3,50.021 7,106.616 0 美元,用户总成本为234.022 0 美 元,LA 的 市 场 收 益 为23 538.434 5 美元。LA 签订负荷平抑合同需将最大负荷控制在阈值内,若LA 不调节响应,电网购买负荷平抑服务的价格将降低,LA 收益下降为21 332.874 5 美元。为此,LA 将调整响应价格曲线优化用户响应。LA 首次更改超阈值的时段价格并发布给用户,激励用户优化响应,调整后的负荷曲线如图2(a)所示,LA 定价变化量和用户响应电量变化量如图2(b)所示。
由图2(b)可见,为降低价格调整增加的成本,用户响应电量与响应时段均发生改变。用户A 谷时段响应变化量最大;用户B 在补偿价格相对高的时段响应变化量最大;用户C 平时段响应变化量最大。调整后的用户成本分别为77.155 3,50.019 5,106.593 9 美元,用户总成本为233.768 6 美元,LA的收益为24 779.360 3 美元。响应价格调整在增加用户响应电量的同时降低用户综合成本、转移用电负荷时段,优化用户响应行为,且LA 的收益得到较大提升,因此LA 将进一步调整定价以优化用户响应,提升自身利润。

图2 负荷平抑响应下的用户负荷与响应电量变化Fig.2 Variation of user load and response power with load smoothing response
用户收益随价格调整而改变,当用户成本超过负荷平抑响应前的成本时退出响应。参与负荷平抑响应的用户数量随响应价格调整次数的变化曲线如图3(a)所示,用户综合成本和LA 收益随响应价格调整次数的变化曲线如图3(b)所示。
从图3(a)可以看出,在前11 次价格调整过程中,所有用户均参与负荷平抑响应,此时用户获得的总体补偿大于用电成本变化。从第12 次电价调整开始,响应用户数量逐步下降,到第20 次时全部退出,表明响应补偿带来的调节空间已全部耗尽。

图3 负荷平抑响应变化Fig.3 Variation of load smoothing response
从图3(b)可以看出,在调整初期,合约用户在谷时增加响应电量,能有效降低用电成本和对用电满意度的影响,同时获得补偿,整体响应电量上升,用电成本逐渐降低。差额响应用户由于峰时折扣价格的升高,为避免过高的用电成本,增加峰时响应电量。随着价格进一步调整,用户响应的优化空间逐渐减小,综合成本逐渐升高,最终与响应前成本一致,全部退出响应。对于LA 而言,随着响应用户数量减少,用户负荷持续升高,LA 的负荷平抑服务价格持续降低,导致收益开始下滑,最终与响应前收益一致。在第11 次价格调整时LA 收益达到最大,此时所有用户参与响应,用户的总成本最低。
4.2 最优定价策略分析
最优定价策略下的总负荷曲线调整结果如图4(a)所示,可见,用户的总负荷曲线中超限时段由17 个减少为3 个,且超限电量明显降低,负荷得到有效平抑。此时所有用户均参与负荷平抑响应,用户总成本为230.977 8 美元,LA 收益为39 886.417 8 美元,比响应前收益提高18 553.543 4 美元。同时虽然电网售电收益减少,但尖峰负荷的削减和低谷负荷的增加有助于提升电网运行的安全性与经济性。
图4(b)中显示了最优定价策略下3 类典型用户的响应时段与响应电量,可以看出,用户响应行为的变化主要与偏好相关。A 类用户响应电量随补偿价格和响应时段变化在理想电量附近波动;B 类用户增加负荷时段不响应,削减负荷时段均以最大可调容量响应;C 类用户在价格折扣最大的时段以最大和最小可调容量增加和削减负荷响应。由于LA 在负荷平抑响应中收益获得较大提升,因此LA 将向用户正式发布并执行最优定价策略。最优定价策略下用户与LA 的响应数据如附录A 表A3 所示。

图4 最优定价策略下的用户负荷曲线与响应电量Fig.4 User load curve and response power with optimal pricing strategy
4.3 用户用电弹性分析
在给定的LA 响应定价策略下,影响用户响应决策的关键因素为响应偏好和购电价格。在相同的购电价格下,用户的偏好系数ω 越大,越注重用电方式的满意度,其参与需求响应的调节弹性越小。而在相同的用电偏好下,购电价格越高,则用户用电成本越高。为分析电价及用电偏好对用户响应行为的影响,定义用户的电价弹性Fpri为相同用电偏好下,单位电价升高导致的用户负荷减少;定义用户的用电偏好弹性Fpre为相同电价下,单位用电偏好变大导致的用户负荷增加,分别如式(34)、式(35)所示。

式中:Δe 为单位购电价格变化量;Δω 为单位用电偏好变化量;ΔQ 为负荷变化量。
根据用户在不同电价、偏好下的单时段可调节负荷用电量计算得到用户的电价弹性和用电偏好弹性曲线分别如图5(a)和(b)所示。

图5 用户用电弹性曲线Fig.5 Electricity elasticity curve of users
从图5 中可以看出,用户电价弹性高于用电偏好弹性,即电价变化对用户用电行为的影响大于用电偏好的影响。此外,用电偏好越小,用户受电价影响越显著,呈现线性变化规律。因此,在参与响应时随着补偿价格和购电价格的变化,B 类用户首先退出响应,A 类用户最晚退出响应。根据用电偏好弹性曲线,电价越高时用户受用电偏好的影响越不显著,呈现指数规律递减。因此在谷时,A 类与B 类用户随补偿价格升高响应电量变化较大;在峰时,A 类与B 类用户随补偿价格降低响应电量无较大改变。
5 结语
LA 通过控制辖区内用户的可调负荷资源作为新的市场主体参与多模式的市场竞争和服务。本文依据LA 向电网提供负荷平抑服务的场景,设计了基于价格激励的需求响应机制。在此基础上,构建了LA 与用户的主从博弈模型,并从理论上分析论证了均衡解的存在性。最后,求解最优定价策略,并进行仿真分析,研究得到以下结论。
1)基于价格激励的需求响应机制可以有效实现LA 对区域内用户可调负荷资源的控制,并使得各参与主体的利益最大化。
2)基于主从博弈的最优定价策略在考虑用户用电偏好的同时,进一步优化用户的响应行为,降低用户综合成本,提高需求响应的稳定性和经济性。
3)LA 基于最优定价策略的响应计划控制区域内GDSR 参与市场,可充分调控用户的用电潜力,提升需求响应参与市场的可靠性和竞争力。
在本文的研究中,采用单个LA 与用户博弈的最优定价策略优化GDSR 响应电量。下阶段可进一步研究多LA 在电力市场中的博弈模型,确定各LA 的最优购电报价策略。此外,LA 可根据实际负荷资源的响应特性进行分类建模,为实际电力负荷参与需求响应的优化控制与运行提供指导。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

