基于宽度学习系统的光伏发电功率超短期预测

周 楠，徐潇源，严 正，陆建宇，李亚平

（1. 电力传输与功率变换控制教育部重点实验室（上海交通大学）,上海市200240；2. 国家电网公司华东分部,上海市200120；3. 中国电力科学研究院有限公司（南京）,江苏省南京市210003）

0 引言

近年来,以光伏为代表的可再生能源发电迅速发展,在有效缓解能源危机问题的同时,其出力的随机性和波动性也给电网的安全稳定运行带来了挑战［1］。因此,准确预测光伏发电功率的变化趋势有助于调度部门及时调整调度计划,从而降低光伏并网对系统的负面影响。

光伏发电功率预测按照时间尺度可以分为中长期预测（1 月到1 年）、短期预测（4 h 到3 d）和超短期预测（数分钟到4 h）［2-3］,其中超短期预测能够提供光伏出力的实时变化信息,是本文的研究对象。光伏发电预测方法可分为物理方法［4-5］和统计方法［6-11］。统计方法基于光伏的历史数据建立出力波动特征的数学模型,预测精度较高且不需要光伏的详细物理参数,因而在光伏发电预测中得到了广泛应用。文献［6-7］以辐照度等气象数据作为输入变量,分别采用径向基函数（radial basis function,RBF）和反向传播神经网络（back propagation neural network,BPNN）预测光伏发电功率；文献［8］采用极限学习机（extreme learning machine,ELM）进行光伏发电预测,显著缩短了预测模型的训练时间。相比于传统的时间序列模型,上述基于单层前馈神经网络的方法提升了光伏发电预测精度,但在训练时存在欠拟合、易陷入局部最优等问题。

近年来,各类深度学习算法被应用于光伏发电功率预测,以克服单层神经网络的不足。文献［9］基于小波变换和卷积神经网络（convolutional neural network,CNN）,提高了光伏发电功率的预测精度；文 献［10］将CNN、长 短 期 记 忆（long short-term memory,LSTM）神经网络及两者的混合模型应用于光伏出力短期预测；文献［11］提出了基于深度信念网络（deep belief network,DBN）的光伏出力日前预测模型。相比于单层网络,深度神经网络表现出更高的预测精度,但其复杂的网络结构也带来了训练耗时、调参困难等问题。对此,文献［12-13］提出了宽度学习系统（broad learning system,BLS）,并有学者将其应用于风光容量配置［14］和无刷发电机旋转整流器故障分类［15］,在保证计算效率的同时取得了精度较高的计算结果。但是,目前尚未有文献涉及BLS 在光伏发电功率预测中的应用。

文献［6-11］主要探讨光伏发电功率的预测算法,但在不同天气类型和出力水平下均采用单一预测模型,导致阴雨天气下的预测误差相对较大。考虑到光伏发电与气象因素密切相关,有文献首先按天气类型对历史数据进行分类,然后针对不同类别分别建立预测模型。文献［16-18］采用自组织映射（self-organizing map,SOM）、K 均值聚类等聚类算法对天气类型进行划分,进一步采用BPNN 等算法预测光伏出力；文献［19］首先采用Adaboost 改进的K 近邻算法实现历史数据聚类,然后建立多阶加权马尔可夫链预测辐照度和光伏出力。按天气类型进行聚类能有效提升光伏发电预测精度,但是现有方法一般以日为单位进行聚类,没有考虑小时乃至分钟级别的光伏出力波动特征,故对于光伏发电功率超短期预测的参考价值有限。

本文提出了一种基于SOM 与BLS 的光伏发电功率超短期预测模型,旨在解决现有研究中光伏数据聚类较为粗糙、深度神经网络训练耗时的问题。首先,以单个时刻的数据样本为单位,综合考虑时间、历史出力、气象条件等因素,采用SOM 实现光伏数据分类；然后,针对不同类别构建基于BLS 的光伏发电功率超短期多步长预测模型,通过网络宽度上的扩展提高网络性能,使得预测模型同时具有强拟合能力与高训练效率；最后,采用实际光伏数据进行算例分析,验证本文所提方法的有效性。

1 基于SOM 的光伏数据聚类

光伏发电具有间歇性与随机性的特征:一方面,在不同时刻和天气类型下,光伏出力曲线具有不同特点；另一方面,辐照度等气象因素的快速变化会导致光伏出力的瞬时波动。如果仅采用单一预测模型,而没有考虑不同天气条件下光伏出力的特性,会导致阴雨天气等情况下的预测误差较大。因此,本文在建立光伏发电功率预测模型前,首先采用SOM神经网络对光伏数据进行聚类分析。

SOM 的神经网络结构如附录A 图A1 所示［20］。它由输入层和输出层（也称为竞争层）组成,其中输入层对应一个N 维的输入向量,竞争层由M=RC 个神经元组成,排列成R 行C 列,构成一个二维平面阵列。竞争层的各神经元之间相互竞争以求被激活,最终在每个时刻仅有一个神经元被激活,称为获胜神经元,该神经元就表示了对输入向量的分类结果。

为了更精准地捕捉光伏发电功率在超短期时间尺度内的波动特性,本文以每个时刻为单位生成光伏数据样本,设时刻t 对应的样本为x（t）∈RN,并利用SOM 对其进行聚类分析。考虑实际应用中可获取的量测数据,本文选取的x（t）包括时刻t 对应的时间戳、邻近时刻的历史气象数据和历史出力、未来辐照度预测值等。因此,如果同一天的不同时刻对应的历史出力波动情况及未来辐照度变动趋势差异较大,也会被SOM 划分到不同的类别,进而采用不同的预测模型获得其未来出力。

在此背景下,SOM 的具体训练步骤如下。

步骤1:算法初始化。对竞争层每个神经元相关的权重向量wi∈RN（i=1,2,…,M）随机赋初值,令迭代次数k=1,并指定最大迭代次数K。

步骤2:向量归一化。给出一个新的输入样本x∈RN,并将wi和x 全部进行归一化处理。

步骤3:寻找获胜神经元。将竞争层中所有神经元的权重向量与输入向量进行比较,将其中距离最小者判定为获胜神经元,相应的权重向量记作wc。对于连续型变量而言,通常采用欧氏距离,即

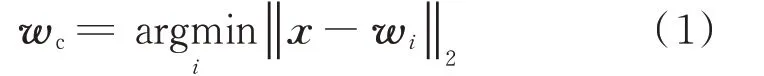
式中:||·||2为L2范数。

步骤4:网络权重调整。对于获胜神经元邻近区域内的神经元,按照下式更新权重,使其向x靠拢:

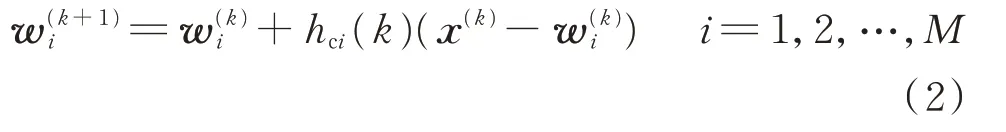
式 中:x(k)和分 别 为 第k 次 迭 代 时x 和wi的值；hci（k）为权函数,与迭代次数及神经元与获胜神经元的距离有关,有

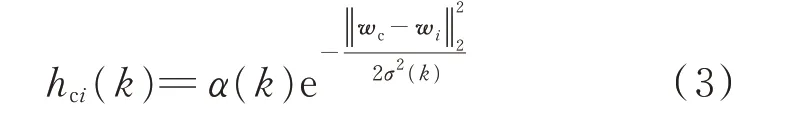
式中:α（k）为学习率；σ（k）为神经元影响半径。这2 个参数均随迭代次数k 的增加而递减。

步骤5:更新输入样本。提供新的输入样本x 给SOM 网络的输入层,返回步骤3,直到将所有样本全部提供给网络。

步骤6:判断算法是否收敛。令k=k+1,返回步骤2,直至相邻2 次迭代的权值误差小于允许值,或者达到预先指定的迭代次数K。

SOM 的竞争层神经元和邻域内的神经元相连,互相激励进行学习,故训练后邻近神经元具有相似的权重。因此,具有相似特征的输入样本映射在邻近 的SOM 输 出 节 点 上［21］。在 利 用SOM 对 光 伏 数据进行精细化聚类后,针对不同的类别形成各自的数据集并分别训练预测模型,可以更好地拟合不同情况下光伏发电功率和相关因素的关系,以提高预测精度。

2 BLS

人工神经网络具有较强的非线性拟合能力,是当前光伏发电功率预测研究中最常用的方法之一。但是传统的单层前馈神经网络在训练时容易收敛到局部最优,导致预测误差较大。因此,近年来各类深度学习算法在光伏出力预测问题中获得了广泛应用［9-11］。尽管深度网络性能强大,但其结构复杂,具有大量的参数和超参数,训练过程极为耗时。针对这一问题,文献［12-13］提出了BLS,在保证神经网络拟合精度的同时,显著提高了算法的训练速度。

2.1 基于LASSO 的稀疏学习

BLS 是基于随机向量函数连接神经网络（random vector functional-link neural network,RVFLNN）［22］构建的。与直接接受输入数据并建立增强节点的传统RVFLNN 不同,BLS 首先对输入进行特征提取以得到一组特征节点。由于稀疏特征学习计算效率高且能有效地表达数据集的特征［23］,故本文采用基于最小绝对收缩和选择算子（least absolute shrinkage and selection operator,LASSO）的稀疏学习实现BLS 特征节点的构造。

为了从给定的输入数据中提取稀疏特征,考虑求解式（4）所示的优化问题:

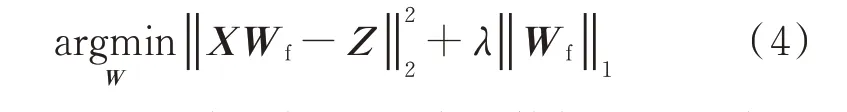
式中:X 为要进行特征提取的输入数据；Wf为特征选择的系数矩阵；Z 为随机生成的特征矩阵。式（4）的第1 项用于求解线性方程XWf=Z 的最小二乘估计；第2 项为L1范数,用于对Wf施加稀疏性限制；λ为正则化参数,用于控制2 项之间的相对大小。该优化问题即为LASSO 回归,可以采用交替方向乘子 法（alternating direction method of multipliers,ADMM）求解［24］。

通过引入辅助变量V,式（4）等价表示为:

该优化问题的增广拉格朗日函数为:

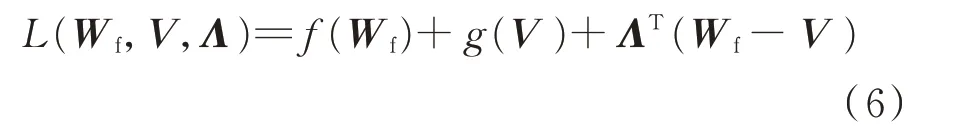
式中:Λ 为该优化问题的拉格朗日乘子。基于ADMM,可以交替更新Wf,V 和Λ 的值来求解式（5）。迭代过程如下:

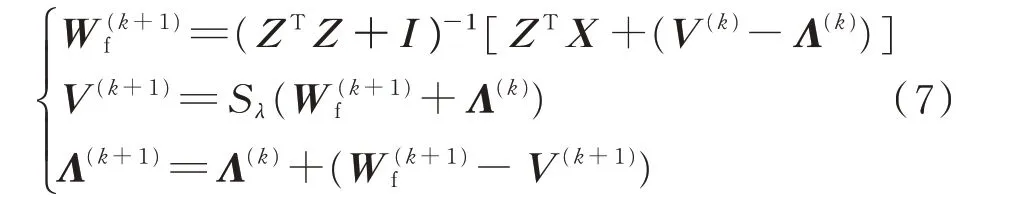
式中:I 为单位矩阵；S 为软阈值函数,其表达式见式（8）。

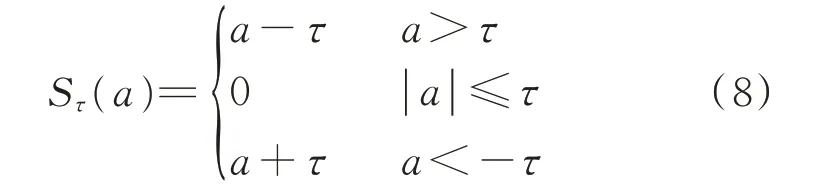
综上所述,输入因素的特征提取只需根据式（7）进行迭代计算即可。

2.2 BLS 的数学模型

BLS 的神经网络结构如图1 所示。由输入数据进行特征提取得到的特征映射构成了特征节点（feature node）,之后特征节点通过非线性变换生成了增强节点（enhancement node）,特征节点和增强节点均与输出层直接连接。BLS 是全连接神经网络,为了简洁表示BLS 结构,图1 省略了每个神经元间的连接。不同于深度学习通过增加神经网络的层数来提高拟合能力,BLS 通过特征节点和增强节点在宽度上的扩展来增强网络性能,这种扁平化的网络结构使其保留了RVFLNN 训练快速的特点。

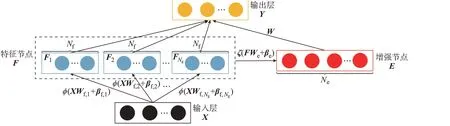
图1 BLS 网络结构Fig.1 Network structure of broad learning system

设图1 中的BLS 包括Ng组特征映射（每组包含Nf个特征节点）和Ne个增强节点。输入矩阵X 由各时刻光伏发电功率预测所需的输入因素向量构成,设共有L 个时刻（记作t1,t2,…,tL）的样本数据,则X=［x（t1）,x（t2）,…,x（tL）］T。X 首先通过特征提取得到一系列特征节点,其中第i 组特征映射由下式得到:

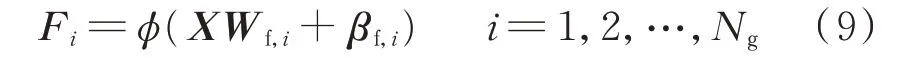
式中:与特征节点相关的权重矩阵Wf,i和偏置项βf,i均随机生成,各元素的取值范围为［-1,1］；映射函数φ 由式（7）间接给出。

将这些特征映射的组合记作矩阵F=［F1,F2,…,FNg］,这NgNf个特征节点根据式（10）生成BLS 的增强节点:

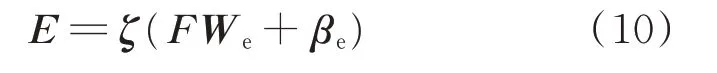
式中:与增强节点相关的权重矩阵We和偏置项βe也是随机生成,各元素的取值范围为［-1,1］；ζ 为激活函数,这里选取双曲正切函数,其表达式见式（11）。

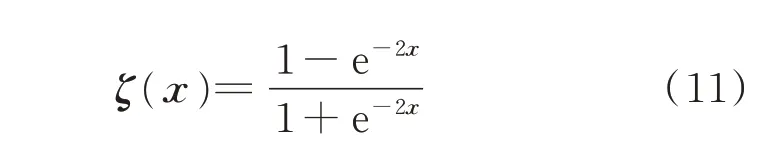
综上所述,BLS 的数学模型可表示为:

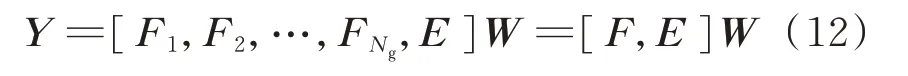
式中:W 表示从特征节点和增强节点连接到输出层的权重；Y 为神经网络的输出,在光伏预测模型中即为预测值。由于超短期预测需要对未来4 h 内的出力进行多步长预测,因此各时刻对应的输出数据为一向量,即Y=［y（t1）,y（t2）,…,y（tL）］T,其中

式中:y（t）为t 时刻的光伏发电功率；Nhor为超短期预测的步长数。为了简化表达式,将BLS 中间层（包括特征节点和增强节点）对应的矩阵记作H=［F,E］。

在训练过程中,随机生成的权重Wf,i与We、偏置βf,i与βe均不再改变,故只需要求解输出权重W即可。因此,BLS 的训练相当于求解线性系统Y=HW 的最小二乘解:

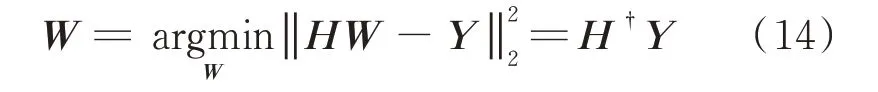
式中:H†为矩阵H 的Moore-Penrose 广义逆矩阵,也称为伪逆（pseudoinverse）矩阵。

可见,BLS 训练不需要基于梯度下降的学习算法,并且训练速度较快、不易陷入局部最优。对于光伏发电功率超短期预测而言,数据采样间隔较小,故训练集规模较大。此外,每个时刻对应着多种气象条件和多点历史出力等相关因素,且进行多步长预测还需要输出多个数值,因此网络输入层和输出层的维度都很高。在此背景下,采用单隐藏层结构、在宽度上扩展节点数目的BLS 作为预测工具,能够较好地拟合历史数据并保证模型计算效率。

3 基于SOM-BLS 的光伏发电超短期预测

对于光伏发电功率超短期预测,数据采样间隔一般为1 min 或5 min,并预测未来若干小时的发电功率,因此需要进行多步长预测［25］。本文利用BLS扁平化的结构特点,构造多输出的神经网络。以5 min 间隔为例,预测未来4 h 内的光伏发电功率,因此构建输出层维度为48 的BLS。

在预测模型输入因素的选取上,本文的具体思路如下:文献［26］提出的Hottel 模型能够预测任意地区全年的晴天太阳辐照度,而非晴天辐照度可由天气类型系数计算得到,预测误差可达到5% 以内［19,27］,因此本文将辐照度实测值叠加±5%的随机误差,假设该数值为辐照度预测值并作为模型的输入因素之一；由于数值天气预报的时间间隔较长且存在一定的滞后,故本文没有将天气预报数据作为预测模型的输入,仅将相邻时刻光伏站点的本地测量气象数据作为参考。此外,光伏发电功率超短期预测通常采用若干个邻近时刻的历史出力作为输入因素［28］,这些历史数据和当前时刻出力之间具有较强的相关性,可以显著提高预测精度。综上所述,首先,应基于气象数据、历史出力等构建特征向量,对各时刻进行精细化聚类；然后,将这些因素进行组合,作为光伏发电功率预测的输入因素。

基于上述思路,本文提出基于SOM-BLS 的光伏发电功率超短期预测模型,如图2 所示。

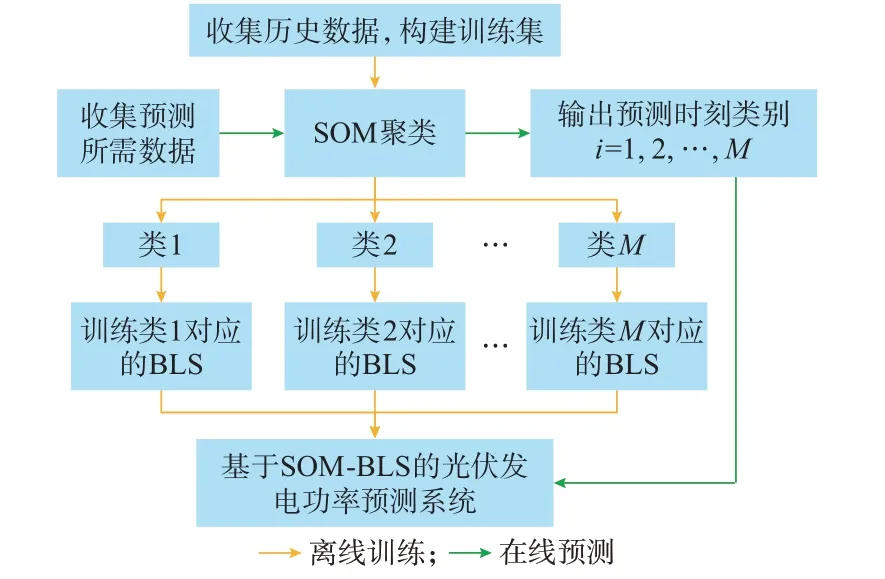
图2 基于SOM-BLS 的光伏发电功率预测系统框架Fig.2 System framework of photovoltaic power generation forecasting based on SOM-BLS

设待预测光伏电站所能提供的气象数据包括水平面总辐射强度（global horizontal irradiance,GHI）、水平面散射辐射强度（diffuse horizontal irradiance,DHI）、法向直射辐射强度（direct normal irradiance,DNI）、风速、气温,且上述气象数据和光伏发电功率数据的采样间隔均为τ,则光伏发电功率预测的具体流程如下。

1）利用SOM 对历史数据进行聚类分析。对于每个时刻t,将对应的时间、邻近Nlag个时刻的历史出力、上一个时间点的历史气象数据（包括辐照度）、未来Nlead+1 个时刻的辐照度预测值作为特征向量x（t）,即

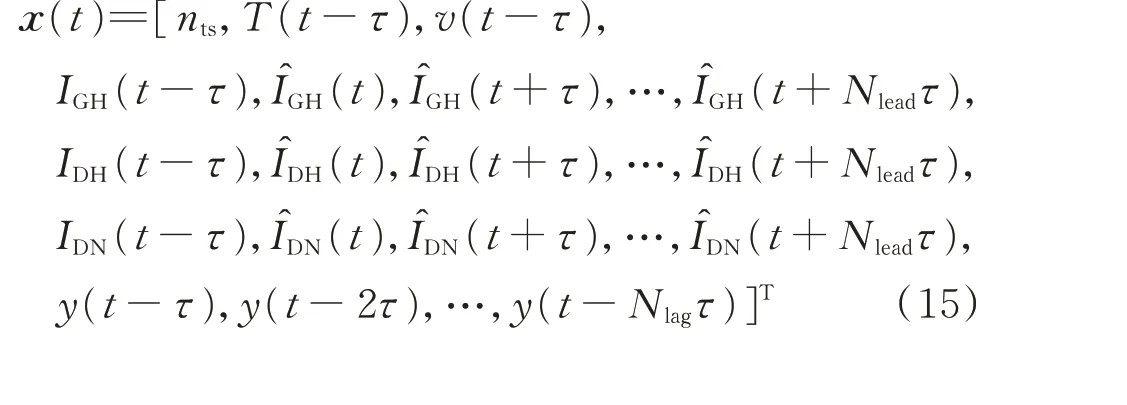
式 中:nts为 时 刻t 在 当 天 的 时 间 戳；T 为 气 温；v 为 风速；IGH,IDH和IDN分别为GHI,DHI 和DNI 的实测值；和分 别 为GHI,DHI 和DNI 的 预 测 值；Nlag和Nlead采用交叉验证法确定。利用历史数据对应的x（t）对SOM 进行训练,并输出每个时刻所属的类别。

2）分类训练BLS。将数据集按SOM 给出的聚类结果进行划分,并分别训练BLS,利用网格搜索法确定其参数Ng,Nf和Ne的最优取值。设训练集中共有L 个时刻（记作t1,t2,…,tL）的样本数据,则BLS的输入矩阵为Xtrain=［x（t1）,x（t2）,…,x（tL）］T,输出矩阵为Ytrain=［y（t1）,y（t2）,…,y（tL）］T。将Xtrain代入式（9）与式（10）中,可得到相应的中间层矩阵Htrain,之后通过式（14）即训练得到BLS 输出权重W。

3）光伏发电功率的在线预测。对于要进行预测的时间断面,按照式（15）的格式建立相应的特征向量,并输入SOM 以判断其类别。之后,将该时刻的特征向量作为对应类别下BLS 的输入,得到预测结果。设测试集中共有R 个时刻（记作tL+1,tL+2,…,tL+R）的样本数据,则BLS 的输入矩阵为Xtest=［x（tL+1）,x（tL+2）,…,x（tL+R）］T,输出矩阵为Yˆtest=[ yˆ(tL+1),yˆ(tL+2),…,yˆ(tL+R)]T,其 中yˆ(t)为 在t 时刻对未来Nhor个步长的发电功率的预测值所构成的向量,即

式中:yˆ(t)为t 时刻的光伏发电功率预测值。

BLS 的训练流程如图3 所示,本文采用标准化均方根误差（normalized root-mean-square error,nRMSE）对预测误差进行评价分析,其表达式为:

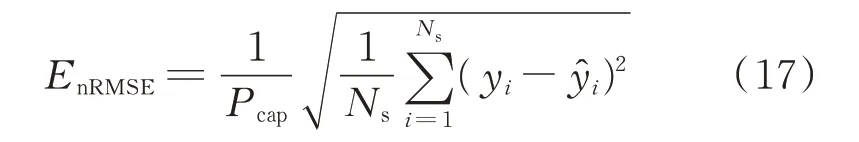
式中:Ns为样本总数；Pcap为光伏发电系统装机容量；yi为实测值为预测值。为体现预测步长对预测误差的影响,本文对不同的预测时间尺度分别计算nRMSE。

4 算例分析

4.1 数据集介绍

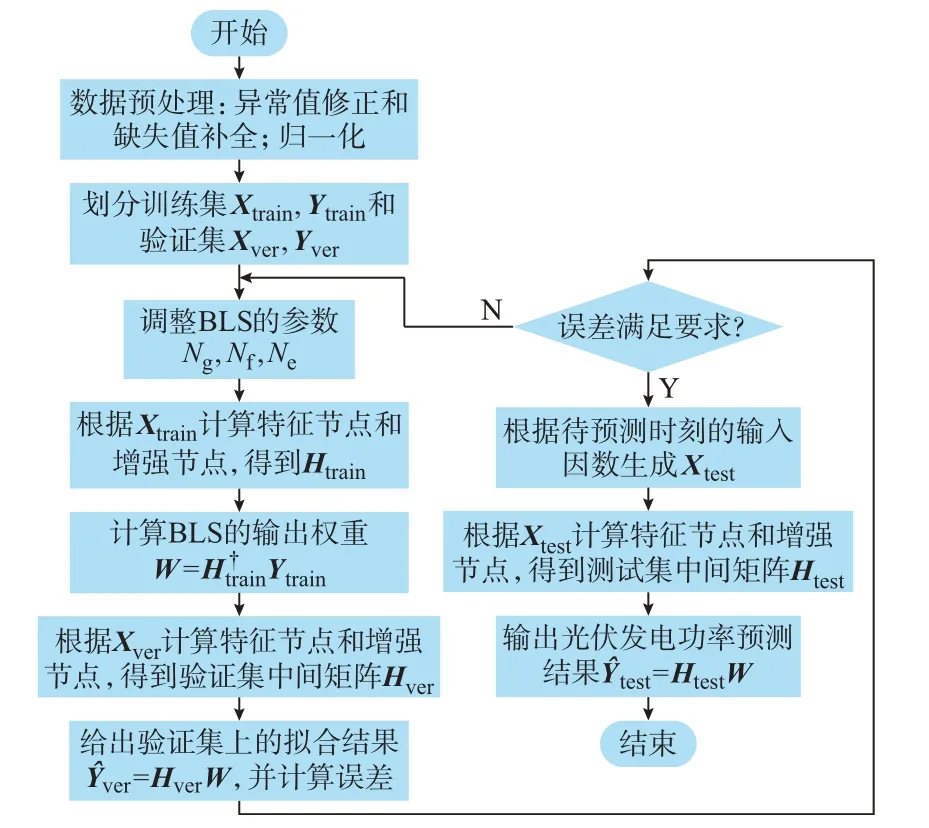
图3 BLS 训练流程图Fig.3 Flow chart of training for broad learning system

为了验证本文提出的基于SOM-BLS 的光伏发电功率超短期预测模型的性能,采用美国俄勒冈州阿 什 兰（Ashland）［29］和 澳 大 利 亚 艾 利 斯 斯 普 林 斯（Alice Springs）［30］的2 处光伏电站数据进行算例分析,并将这2 组数据集分别简称为算例1 和算例2。2 组算例的光伏信息、数据格式与预测模型输入输出选取如附录A 表A1 所示,其中输入因素的辐照度预测值点数与历史发电功率点数均采用5 折交叉验证确定。对于数据集中的异常值和缺失值,利用该采样点前3 个时刻的平均值替代［31］。考虑到光伏出力的间歇性,截取白天时段后算例1 保留05:20—19:15 的数据,即每日有168 个数据点,时间戳取值范围为0～167；算例2 保留07:15—18:25 的数据,即每日有135 个数据点,时间戳取值范围为0～134。收集算例1 在2017—2019 年每年6—8 月的气象数据和光伏出力数据作为数据集,其中2019 年8 月的数据作为测试集（共5 208 个样本）,其余8 个月数据作为训练集和验证集（共41 160 个样本）；收集算例2 在2016—2018 年每年6—8 月的气象数据和光伏出力数据作为数据集,其中2018 年8 月的数据作为测试集（共4 185 个样本）,其余8 个月数据作为训练集和验证集（共33 075 个样本）。进行预测前,对预测模型输入因素和输出变量均进行归一化处理。

本文采用MATLAB R2018a 编程实现基于SOM-BLS 的光伏发电功率超短期预测模型,计算环境为2.21 GHz 主频英特尔酷睿i7-8750H 处理器、8.00 GB 内存的计算机。

4.2 SOM 聚类效果对比实验

对于算例1,根据式（15）生成特征向量,并将其作为SOM 的输入,对数据集进行聚类分析。经过交叉验证,式中Nlag=18,Nlead=47,即SOM 输入层节点个数为N=168,即与每个时刻相关联的输入因素（时间戳、历史出力、历史气象数据和辐照度预测值）共168 个。同理可以列出算例2 的特征向量表达式,相应的Nlag=15,Nlead=47,即SOM 输入层节点个数为N=117。

当SOM 竞争层节点个数选取为M=4×3 时,可对数据集充分进行分类且保证每一类都有足够样本。SOM 的聚类结果可由竞争层的拓扑结构直接得到,聚类后的样本分布如附录B 图B1 所示。为反映聚类结果的物理意义,在二维坐标系中绘制各时刻的发电功率-时间散点图,以算例1 在2018 年7 月的数据为例,结果如附录B 图B2 所示。可见,SOM聚类能够将时刻、出力水平相近的样本划分在同一类中,进而提升BLS 的拟合效果、减小预测误差。

为了定量验证SOM 聚类对于预测精度的影响,将未进行聚类的数据作为BLS 的输入,对未来4 h 内以5 min 为步长的48 个时刻进行发电功率预测,并与SOM-BLS 预测模型进行对比。不论是否进行聚类,均采用交叉验证方法确定BLS 的参数。未聚类时,算例1 中BLS 的最优参数为:Ng=44,Nf=11,Ne=174；算例2 中BLS 的最优参数为:Ng=12,Nf=10,Ne=264。进行聚类后,2 组算例各自的12 组BLS 最优参数如附录A 表A2、表A3 所示。算例1 聚类前后各时间尺度下的预测误差nRMSE 见表1（预测结果为48 个点,这里只列出了具有代表性的几个时间尺度）,算例2 相应的实验结果如附录A 表A4 所示。

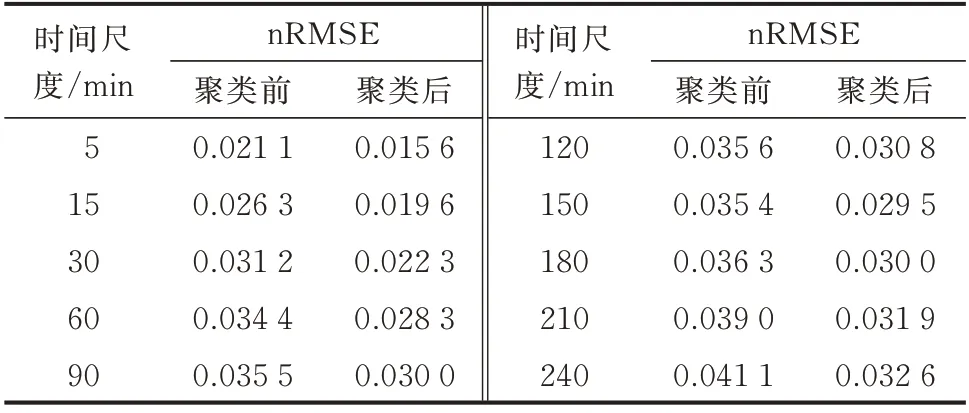
表1 算例1 聚类前后预测误差nRMSE 比较Table 1 Comparison of nRMSE in case 1 before and after clustering

此外,还可以将预测值和实际值绘制在同一坐标图中,以更直观地对比聚类前后的预测效果。本文针对单个时间断面,对未来4 h 的出力进行多步长预测。以每日的08:00 和12:00 为例,聚类前后的预测结果见附录B 图B3 至图B6。此外,现有文献在进行光伏发电功率超短期预测时,一般以日为单位,对每个时刻进行相同时间尺度的预测,滚动预测后得到该日的出力曲线。为方便与现有工作进行对比,聚类后的滚动预测结果（选取1 h,2 h,3 h 和4 h这4 种时间尺度）分别如附录C 图C1 至图C4 所示。从上述实验结果可以看出,利用SOM 对数据集进行聚类、分类训练模型,可在一定程度上提升各时间尺度下光伏发电功率的预测精度。

4.3 BLS 预测性能对比实验

为了验证BLS 在光伏发电功率超短期预测上的优越性,选择BPNN,ELM 和LSTM 神经网络3 种方法进行对比。各模型均在SOM 聚类的基础上进行预测,其中BPNN 和ELM 的参数设置分别如附录A 表A5 和表A6 所示。LSTM 的超参数数目较多,故对于不同类别均设置相同的参数,其中算例1:LSTM 层具有260 个隐藏节点,全连接层具有160 个节点；算例2:LSTM 层具有200 个隐藏节点,全连接层具有135 个节点。训练LSTM 时设置学习率为0.01,批尺寸为20。

上述3 种方法和本文提出的SOM-BLS 模型的预测误差对比如表2 和表3 所示,训练时长（包括SOM 神经网络的训练耗时）对比如表4 所示。此外,选 取 算 例1 中8 月2 日 和8 月9 日、算 例2 中8 月7日和8 月30 日绘制预测出力曲线,预测结果与实际值对比如图4、图5 及附录C 图C5、图C6 所示。

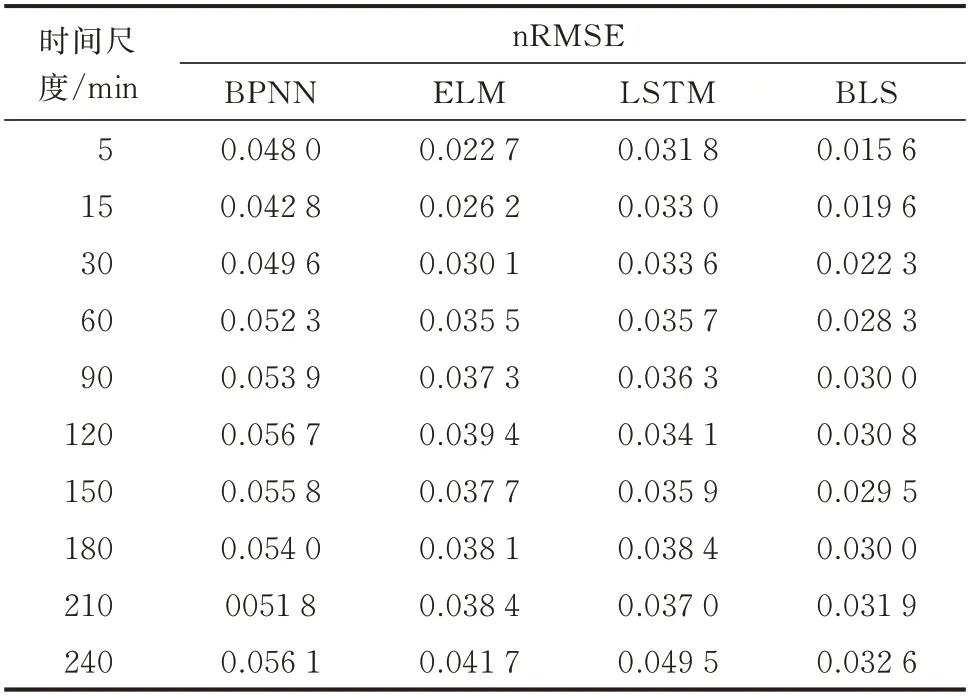
表2 算例1 各模型预测误差nRMSE 比较Table 2 Comparison of nRMSE in case 1 among different models

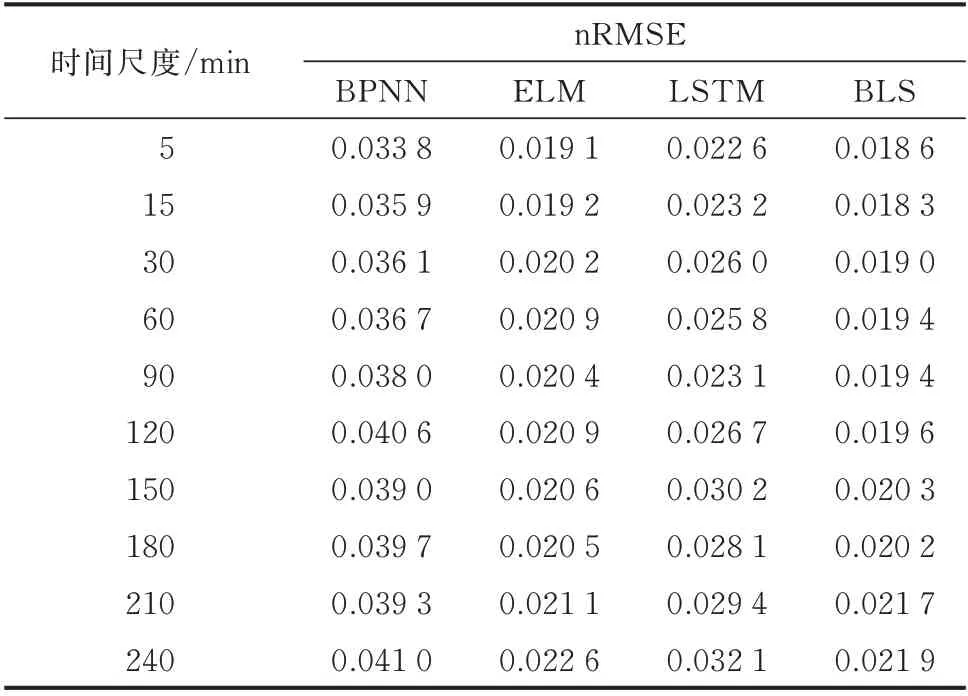
表3 算例2 各模型预测误差nRMSE 比较Table 3 Comparison of nRMSE in case 2 among different models

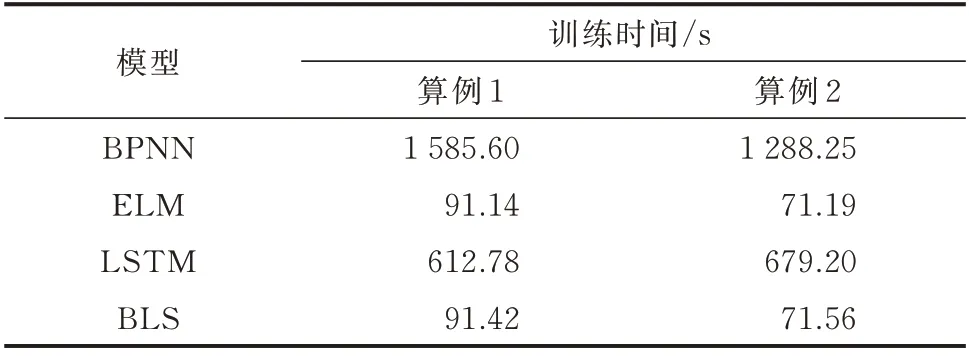
表4 各模型训练时间比较Table 4 Comparison of training time among different models

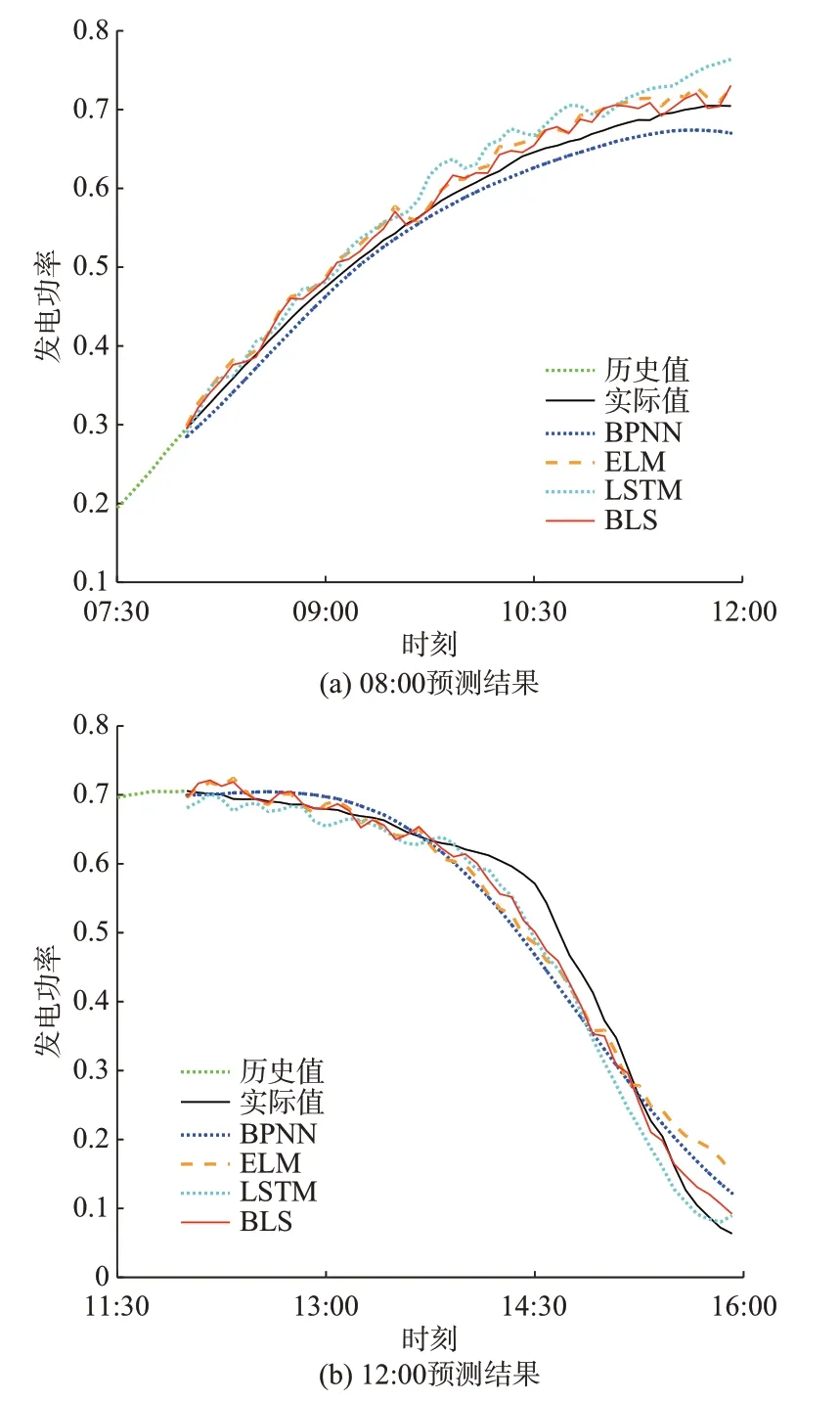
图4 算例1 各模型预测结果对比（8 月2 日）Fig.4 Comparison of forecasting results in case 1 among different models on August 2

由表2 与表3 可见,在不同时间尺度下BLS 的预测误差均最小。4 种方法中,BPNN 的误差最大,且预测精度随步长的增加显著降低,说明当输入、输出维度较高时,该神经网络的拟合性能不足。LSTM 作为深度神经网络,其预测误差较BPNN 显著改善,但仍存在着步长较大时预测精度不足的问题。ELM 与BLS 的结构类似,故两者预测误差随步长的变化趋势相似；BLS 对输入数据进行了特征提取,能够更准确地拟合高维变量间的关系,故其预测误差在各时间尺度下均小于ELM。

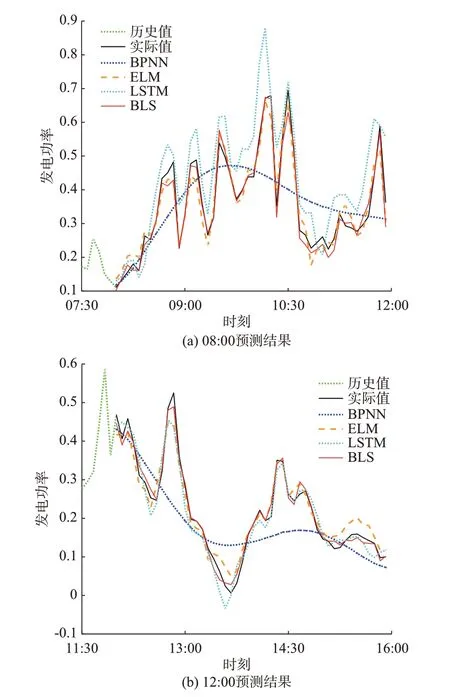
图5 算例1 各模型预测结果对比（8 月9 日）Fig.5 Comparison of forecasting results in case 1 among different models on August 9

从图4、图5 及附录C 图C5、图C6 可以看出,针对不同的光伏电站和天气类型进行预测时,BLS 的预测结果均能较好地跟踪未来4 h 内光伏发电功率的波动趋势。具体来说,4 种对比方法在预测晴天时误差较小,但在预测12:00—14:00 的出力时,BPNN 和ELM 在 算 例1 上、BPNN 和LSTM 在 算 例2 上的误差随着步长的增加显著增大；在预测阴雨天时,BPNN 的误差很大,不具有参考价值,而LSTM 与ELM 虽能在一定程度上跟踪光伏的出力波动,但是大部分时间尺度下的预测误差均大于BLS。

在训练时长上,ELM 和BLS 的训练均是基于伪逆运算、不需要迭代求解,故计算效率很高,可以适应超短期预测在线更新模型参数的要求。而BPNN 在处理高维度、大规模的数据时会面临“维数灾”问题［32］,导致神经网络的拟合精度和训练速度显著下降；而LSTM 作为深度学习算法,在训练时要确定大量的网络参数［33］,因此这2 种方法的训练过程极为耗时,当数据集更新时难以及时对模型进行重新训练。

基于上述讨论,本文提出的SOM-BLS 模型在光伏发电功率超短期预测中体现出较高的预测精度与计算效率。

5 结语

本文提出了一种基于BLS 的光伏发电功率超短期预测模型。首先,基于各时刻的气象条件、历史出力等数据构成特征向量,采用SOM 神经网络进行聚类分析；然后,按照聚类结果划分数据集并分别训练BLS,对发电功率进行多步长预测；最后,采用光伏电站的实际运行数据进行测试,得出以下结论。

1）基于SOM 神经网络的精细化聚类能够捕捉光伏发电在不同时刻的出力水平和波动特征,在相同条件下较未进行聚类分析的方法能够有效提升预测精度。

2）在进行多步长预测时,BLS 具有较高的预测精度,能够在不同时段和天气类型下较好地跟踪光伏发电功率的变化趋势。

3）BLS 具有较高的计算效率,在超短期预测这一应用场景下,相比于LSTM 等深度学习算法,具有能够在线更新参数的优势。

下一步工作将考虑光伏发电的时空相关性以进一步提高预测精度,并利用BLS 的结构特点开展概率预测,更准确地刻画光伏发电的不确定性。

本文得到华东电网科技项目“大电网源网荷储泛在调度的市场机制及商业模式研究”的资助，特此感谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。