基于天气分型的短期光伏功率组合预测方法
叶 林,裴 铭,路 朋,赵金龙,何博宇
(中国农业大学信息与电气工程学院,北京市100083)
0 引言
太阳能是一种清洁的可再生能源,随着全球对清洁能源的需求不断增长,光伏发电将发挥重要作用[1]。在过去的几十年中,光伏发电受到越来越多的关注[2-4],光伏发电的整合带来了显著的经济和环境效益。然而,由于其不确定性和间歇性,光伏发电的高渗透率也给现有电网系统的运行带来了许多新挑战[5]。这些挑战包括光伏电源对气象条件的敏感性,高安装成本以及发电的间歇性[6]。提升光伏功率预测的精度是克服这些挑战的有效解决方案。
按预测时长来分,光伏功率预测包括超短期预测(15 min 至4 h)、短期预测(4 h 至3 d)、中期预测(3 d 至1 个月)和长期预测(1 个月以上)[7],其中短期光伏功率预测是本文的研究对象,准确的短期光伏功率预测对提升电力系统的可靠性及电力系统对光电的消纳能力具有重要意义。对于光伏系统,光伏阵列所接收的太阳光谱辐照度通常会受到其他气象因素的影响,因此不同天气条件下的光伏功率波动特征不同[8]。这意味着光伏功率预测精度不仅取决于所选择的预报模式,而且还取决于天气状况。因此,研究人员对基于天气分型的光伏预测模型越来越感兴趣,以便准确预测由于天气模式不同所造成的光伏输出功率的不确定性和波动[9-10]。然而,很少有文献在考虑深度学习模型特点的基础上,研究不同天气类型的功率波动物理特征及相关气象因子的识别。大多数文献只是简单地选择一种分类器来完成分类任务,而不知道该分类器是否适合基于收集到的天气数据进行分类任务[11]。文献[12]应用自组织映射(self organizing map,SOM)和学习矢量量化(learning vector quantization,LVQ)对分类阶段收集的光伏发电输出历史数据进行分类。文献[13]提出了一种基于太阳辐照度特征提取和支持向量机(support vector machine,SVM)的短期光伏功率预测天气状态模式识别模型。另外,神经网络训练样本的数据质量以及数值气象预报(numerical weather prediction,NWP)因素的选取也会影响光伏功率短期预测的精度[14]。文献[15]利用iForest 算法剔除神经网络训练集中存在的异常数据。文献[16]利用Pearson 相关系数选取NWP 数据集中与光伏功率相关的因素,作为预测模型的输入量。文献[17]基于聚类算法将光伏功率按照天气状况分为晴天、阴天、雨天,分别建立了分钟级波动与小时级波动的理论公式。在保证神经网络训练样本数据质量的基础上,光伏功率波动特征的准确预测对提升光伏功率预测精度具有重要意义[18]。
基于上述分析,本文提出基于天气分型的短期光伏功率组合预测方法,首先基于NWP 将预测模型分为5 类,可以直接将气象因素作为选择预测模型的基准;定义光伏日功率序列波动参数,基于四分位法对气象因素与功率波动特征进行匹配,一定程度上解决了NWP 数据与光伏实测功率数据相关性低的问题,使预测模型中的光伏功率波动特征更加集中;然后基于变分模态分解(variational mode decomposition,VMD)算法分解出功率波动过程和类晴空过程,考虑不同天气情况下功率波动特征的特异性,基于数学算法筛选出各天气分型下NWP相关因子,解决了NWP 数据冗余的问题,同时增强了深度学习网络的学习能力;最后利用深度学习网络对功率类晴空过程和功率波动过程进行分类预测,一定程度上解决了传统预测模型对光伏功率波动特征预测不准确的问题,光伏功率基准值的预测精度也有所提升。算例分析表明,相比于传统的机器学习方法,本文所提方法能够有效地提升短期光伏功率的预测精度。
1 光伏功率波动过程的短期预测基本框架
光伏功率波动特征受天气的影响较大,不同天气类型下光伏功率的波动特征不同。通常短期光伏功率预测是基于NWP 进行预测,预测模型的训练集由历史NWP 和历史光伏功率的时间序列构成。本文首先基于气象特征与光伏功率波动特征相关联的天气划分模型,将天气类型分为晴天、阴天、多云、全雨、阵雨5 种类型,其中,阴天、多云、全雨、阵雨模型统称为非晴模型。天气分型后的各预测模型数据集特征更加集中,有利于提升预测精度。
为提取出受气象因素影响下的光伏功率波动过程,将非晴模型的光伏电场日输出功率曲线进行VMD,对非晴模型的光伏功率序列选取相应的频段分量进行叠加,分解出各非晴模型的低频信号与高频信号。其中低频信号表示非晴模型的类晴空过程,高频信号代表非晴模型的波动过程。基于天气分型下的波动过程划分结果,本文对NWP 数据与晴天模型、非晴模型的类晴空过程进行Granger 因果关系分析,得出NWP 晴天相关因子,对NWP 数据与非晴模型的波动过程进行Granger 因果关系分析,得出各非晴模型的NWP 波动相关因子。
传统的预测模型是基于NWP 时序和光伏功率时序之间的非线性关系所建立的映射模型,而光伏电场输出功率特征具有昼夜周期性,光伏日功率序列波动过程的预测一定程度上制约了光伏功率预测精度[1]。本文建立以光伏功率波动过程及NWP 相关因子波动过程为输入、以光伏功率波动过程为输出的预测模型,其可以在一定程度上提升预测精度。在预测模型的数据输入中,将筛选出来的NWP晴天相关因子与晴天模型历史功率、非晴模型历史功率类晴空过程作为光伏功率类晴空过程预测模型的训练集;将各天气分型下的NWP 非晴相关因子与各天气分型下的功率波动过程作为光伏功率波动过程预测模型的训练集。对于晴天模型来讲,直接利用NWP 晴天相关因子预测出来的光伏功率即为最终预测值;对于非晴模型来讲,首先利用NWP 晴天相关因子预测出功率类晴空过程,其次利用各天气分型下NWP 波动相关因子预测出功率波动过程,二者叠加即为最终预测值。本文的总体思路框架如图1 所示。
2 波动过程划分及NWP 相关因子筛选
2.1 基于气象因素与功率波动过程匹配的天气分型方法
2.1.1 基于NWP 的天气分型
光伏电场输出功率取决于场站区域光资源即太阳辐照度的分布,而光伏发电单元所接收的太阳辐照度易受到天气类型的影响,不同天气类型下的光伏功率波动特征不同。本文参照短期天气预报国家标准[19],选取NWP 中的云量C、大尺度降水pl、对流降水ps作为天气分型因素,记V =[C,pl,ps]为天气分型向量。考虑到光伏电场输出功率的特征,即只有白天有功率输出、夜晚没有功率输出。本文按照单日白天平均云量区分晴天模型、多云模型及阴天模型,按照单日白天降水时长区分全雨模型与阵雨模型。根据气象划分标准对上述天气分型因子进行预处理。
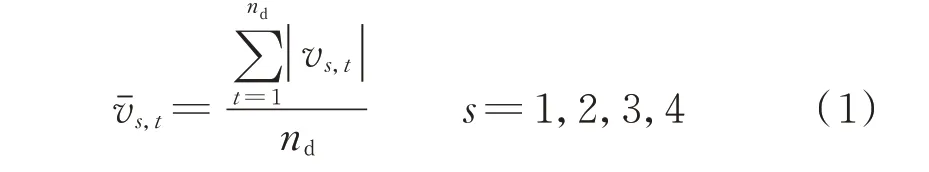
式中:vs,t为第s 个天气分型因子在t 时刻的值;nd为以15 min 为时间间隔的预报下,一天内白天的时间点数量。
2)降水时间定义
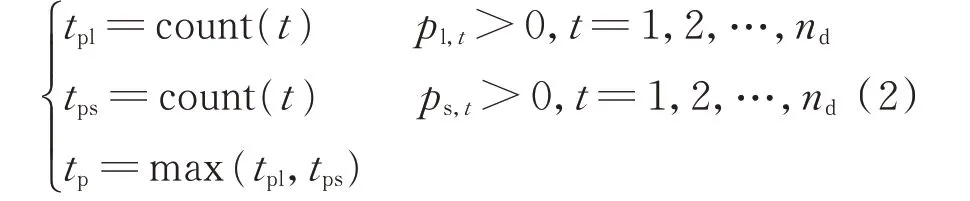
式中:count(⋅)为计数函数,统计序列中符合条件的元素个数;tpl为大尺度降水的时间点数量,当大尺度降水量pl,t大于0 时统计;tps为对流降水的时间点数量,当对流降水量ps,t大于0 时统计;tp为降水时间,取tpl和tps的最大值。
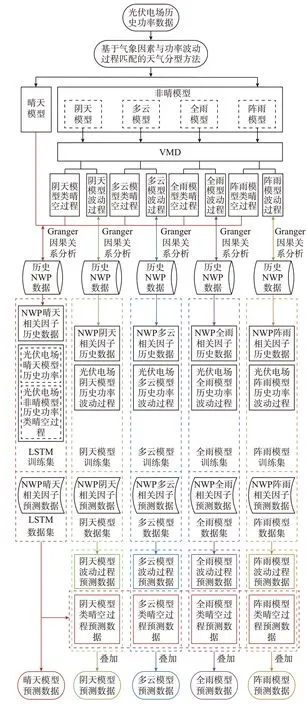
图1 基于天气分型的光伏电场短期功率预测总体框架Fig.1 Overall framework of short-term power forecasting for photovoltaic power station based on weather classification
根据上述天气分型向量的识别与天气分型因子预处理方法,按照晴天模型、多云模型、阴天模型、阵雨模型及全雨模型,给出基于NWP 的天气分型公式,如表1 所示。

表1 基于NWP 的天气分型模型Table 1 Weather classification models formula based on NWP
2.1.2 光伏功率波动过程的定义
基于NWP 对天气分型后,由于短期NWP 的精度有限,各天气分型模型下存在着NWP 误报的异常数据,因此本文基于光伏功率的波动特征对各天气分型的数据进行精确筛选,从而确保深度学习模型训练样本的质量。
为消除光伏功率基数对功率波动参数的影响,本文首先对每日的光伏功率序列进行归一化处理,如式(3)所示。

式中:[·]表示差分运算;Pt为t 时刻的光伏电场功率,本文的目的为识别极值点,此处k=1。
根据光伏功率序列的前向差分与后向差分的结果,按照式(6)和式(7)判断光伏电场日功率序列的极值。
极大值的判别式为:

极小值的判别式为:

基于光伏功率极值判别式,定义光伏日功率序列的波动过程参数如下。
1)光伏日功率序列曲线波动峰值Rm
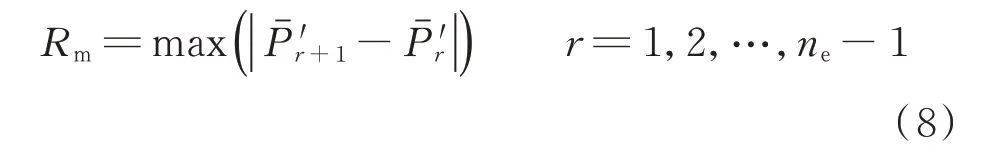
2)光伏日功率序列波动频率f

式中:n 为时间点的总数量,本文取96。
3)光伏日功率序列波动突变率ηm

式中:lr为归一化日功率序列相邻极值点的时间间隔;tr为归一化日功率序列极值点所对应的时刻。
本文以中国吉林省某光伏电场一年的数据为例,得到5 种天气模型下年平均功率波动参数的柱状图与年平均气象分型参数的折线图,见图2。
由图2 可以明显看出,在5 种天气类型下,随着云量、对流降水、大尺度降水的增加,各个功率波动参数也呈单调递增趋势。表明了本文所划分的5 种天气类型可以有效区分功率波动特征,也说明了本文所定义的功率波动参数可以有效刻画不同天气类型下的功率波动特征。
2.1.3 基于四分位法的光伏功率波动过程划分
根据前文定义的光伏日功率序列波动过程参数,记W =[ Rm,f,ηm]为光伏功率波动特征向量。本文基于四分位法确定各天气分型下的光伏功率波动特征向量的阈值,计算方法如下[20]。
1)计算各光伏功率波动特征参数的第2 个四分位数即中位数Q2,G,h,如式(12)所示。
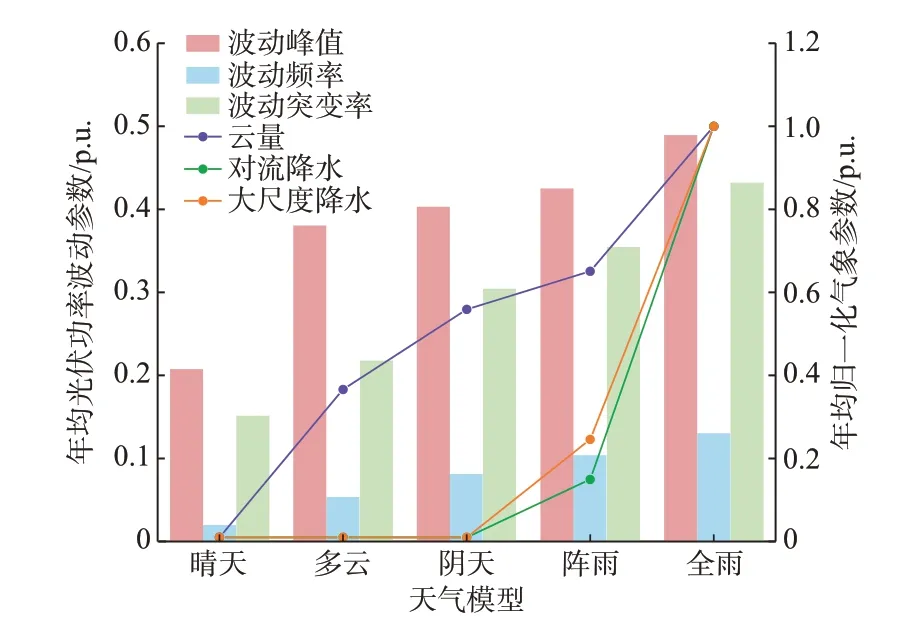
图2 各天气分型下的功率波动参数与天气分型参数对比分析Fig.2 Comparative analysis of power fluctuation parameters and weather classification parameters of various weather types

3)计算四分位矩并确定光伏功率波动特征向量的阈值。
根据式(15)计算各天气模型的光伏功率波动参数的四分位矩IQR,G,h。
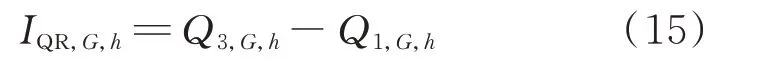
根据式(16)可以确定各天气模型的光伏功率波动参数序列的区间。

式中:F1,G,h为第h 个天气模型下第G 个光伏功率波动特征参数的阈值下限;Fu,G,h为第h 个天气模型下第G 个光伏功率波动特征参数的阈值上限;处于区间[ F1,G,h,Fu,G,h]以外的数据都是异常值。
本文以中国吉林省某光伏电场一年的数据为例,得到晴天、多云、阴天、阵雨、全雨5 种模型的光伏功率波动参数箱线图,如图3 所示。根据四分位法的分析结果,将晴天、多云、阴天、阵雨、全雨5 种天气模型中的异常光伏功率波动参数所对应的光伏功率日序列及NWP 数据剔除,从而使得各天气模型的光伏功率波动特征更为集中,有利于深度学习模型对光伏功率日序列及NWP 数据之间的映射关系进行训练,从而提升光伏功率的预测精度。
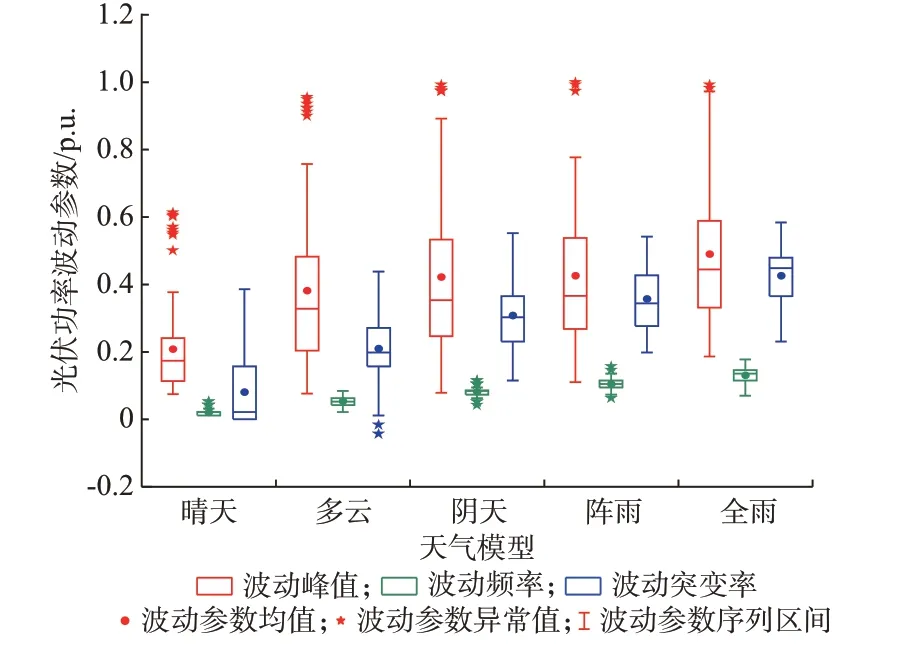
图3 基于四分位法的光伏功率波动参数箱线图Fig.3 Box plot of photovoltaic power fluctuation parameters based on quartile method
2.2 基于VMD 的光伏功率波动过程提取
本文基于气象因素与功率波动过程匹配的天气分型方法将光伏功率预测模型分为5 类,为更好地训练和学习各天气类型下的功率波动特征与NWP数据之间的映射关系,本文基于VMD[21]将非晴模型的光伏功率分解为类晴空过程和波动过程。具体步骤如下。


步骤3:根据步骤1 和步骤2 得到M 个固有模式函数(IMF),第m 个固有模式函数记为IMFm(m=1,2,…,M)。为获取平滑的低频信号以表示类晴空过程,需要确定合适的模态数M。本文用一年的光伏功率曲线作为样本,分别取M=4,5,…,16,对每个M 值对应的IMF1 信号进行快速傅里叶变换,确定其中心频率,当M=9 时可以获取最平滑的低频信号。IMF1 分量作为光伏功率的类晴空过程,IMF2 至IMF9 分量之和作为光伏功率的波动过程。
附录A 图A1(a)至(d)分别展示了多云、阴天、阵雨、全雨模型典型日的功率序列分解结果。可以清晰地看出,光伏序列的波动过程可以更加直观地反映不同天气类型下光伏日功率序列的波动特征。
2.3 基于Granger 因果分析的NWP 相关因子筛选
在光伏功率短期预测领域中,由于时间周期较长,不能和超短期预测一样将辐照度作为唯一的相关因子。图4 为2017 年7 月各天气分型下的光伏功率与短波辐射关系的示意图。

图4 各天气分型下短波辐射与实测功率对比分析Fig.4 Comparison and analysis of short-wave radiation and measured power with various weather types
由图4 可见,短波辐射的短期预报值不能完全反映光伏功率实测值的波动特征,因此必须提取更多与光伏功率波动特征相关的气象因子作为深度学习网络的输入变量,从而提升光伏功率的预测精度。
本文选择Granger 因果分析法对各天气分型下光伏功率的相关气象因子进行筛选。因果关系是基于统计学中的零假设,其原理是因变量的加入有助于结果变量的预测。在时间序列中,如果使用变量序列和目标序列的历史观测值的预测效果要好于仅仅使用目标序列自身历史观测值的预测效果,那么称x 是y 的Granger 因变量或者x 是引起y 变化的Granger 原因[22-23]。
在Granger 因果关系分析中,原因变量是指引起一定现象的变量,结果变量是指由于一定原因的作用而引起现象的变量。因此基于Granger 因果关系分析识别NWP 相关因子时,可以有效剔除以下2 类NWP 因子:一类是与光伏功率毫无关系的气象因素,属于冗余变量;另一类是一定气象因素下造成的结果,不能用于预测光伏功率,属于结果变量。本文采用Granger 因果关系分析可以从多维NWP 气象因素中筛选出光伏功率波动过程及类晴空过程的原因变量。
设光伏功率历史实测数据为{ Pt},NWP 多维气象因素数据为{ xw,t,w=1,2,…,W },W 为NWP气象因素类型数,估计以下2 个回归模型。
有约束回归模型为:
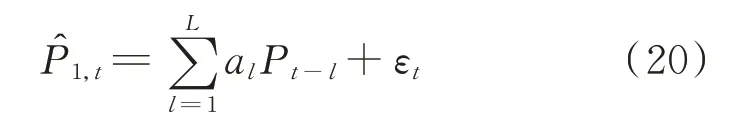
无约束回归模型为:
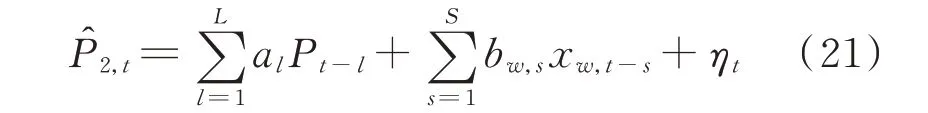
用2 种回归模型计算出光伏功率时间序列的估计值后,基于实际光伏功率序列{ Pt},根据式(22)计算有约束回归模型、无约束回归模型的残差平方和Rr和Ru,基于式(23)构造F 统计量,并使用F 检验判断各NWP 影响因子是否为光伏功率过程的Granger 原因。
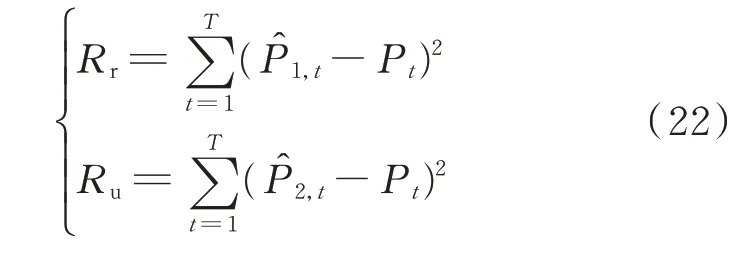

式中:T 为光伏功率序列的样本容量。
检验原假设“第w 个NWP 因子{ xw,t}不是引起光伏功率{ Pt}变化的Granger 原因”。如果F ≥Fα(k,T -s-l-1),应拒绝原假设,即该NWP 因子是引起光伏功率变化的Granger 原因,其中Fα为F 分布α 分位数;反之,则不能拒绝原假设,即该NWP 因子不是引起光伏功率变化的Granger 原因。
按照Granger 因果关系分析的结果,筛选出类晴空过程、各天气分型下波动过程所对应的NWP相关因子。从而完成基于天气分型的光伏电场功率组合预测模型的训练数据准备。
3 光伏功率波动过程组合预测模型
3.1 卷积神经网络-长短期记忆网络组合预测模型
本文基于天气分型下对光伏功率波动过程分解结果,并结合所筛选的NWP 相关因子构成预测模型的基本数据集。 本文采用卷积神经网络(convolutional neural network,CNN)及长短期记忆(long short-term memory,LSTM)网络作为预测模型[24-25],用CNN-LSTM 组合预测模型表示,组合预测模型的数据集结构如图5 所示。
本文所选择的组合预测模型中,CNN 模型主要由2 层卷积层和2 层池化层组成。卷积内核数分别为64 和128,并且在池化层中选择了最大池化模式;LSTM 模型包含2 个隐藏层,每个隐藏层分别具有64 和128 个神经元。由图5 可知,输入、输出数据集中的每个神经元是由以15 min 为时间间隔的96 点所构成的,每个天气类型的模型训练集将训练96 点功率过程与96 点NWP 相关因子之间的映射关系,从而在测试集中一次输出96 点预测功率。其中,训练集中的晴天模型光伏功率、非晴模型类晴空过程及各非晴模型的波动过程数据均为二维数组,以晴天模型光伏数据结构为例,1×96×118 表示晴天模型118 d 的96 点光伏日功率序列;训练集中各天气类型的NWP 相关因子均为三维数组,以NWP 晴天相关因子为例,10×96×365 表示晴天模型和各非晴模型共365 个样本,每个样本包括10 种NWP相关因子的96 点序列。组合预测模型的超参数设置具体见附录B 表B1,光伏功率组合预测模型的具体步骤如下。

图5 光伏功率组合预测模型结构Fig.5 Structure of combined forecasting model of photovoltaic power
步骤1:根据第2 章所提的波动过程划分及NWP 相关因子筛选方法,将待预测光伏电场的历史NWP 数据与历史光伏功率数据分为晴天模型、多云模型、阴天模型、阵雨模型与全雨模型5 种类型,将5 种天气类型下的光伏日功率序列分解为波动过程与类晴空过程,并筛选出5 种天气类型下所对应的NWP 相关因子。此时光伏功率组合预测模型的训练集已完成数据准备。
步骤2:基于LSTM 模型,将晴天模型光伏功率、各非晴模型类晴空过程以及NWP 晴天相关因子的历史数据导入训练集中,完成对类晴空模型训练集的构建。
步骤3:基于CNN 模型,分别将多云模型、阴天模型、阵雨模型及全雨模型的光伏功率波动过程及其所对应的NWP 相关因子的历史数据导入训练集中,完成对4 个非晴模型训练集的构建。
步骤4:输入待预测日的NWP 数据,根据2.1.1 节所提的基于NWP 的天气分型方法判断待预测日的天气类型,若天气类型为晴天模型,则将NWP 数据中的晴天相关因子输入至LSTM 类晴空模型测试集中,即输出待预测日的光伏功率;若天气类型为非晴模型,则一方面将NWP 数据中的晴天相关因子输入至LSTM 类晴空模型测试集中,输出待预测日的光伏功率类晴空过程,另一方面将NWP数据中的非晴相关因子输入至所属天气类型CNN波动模型测试集中,输出待预测日的光伏功率波动过程,将光伏功率类晴空过程与波动过程叠加即为预测功率。
3.2 预测误差评价
本文采用均方根误差(RMSE)、平均绝对误差(MAE)作为误差评价指标。各误差计算公式如下。

式中:Pt,pre为t 时刻的光伏功率的预测值;Cap为光伏电场的装机容量;N 为预测时段。
4 案例分析
本文以中国吉林省某装机容量为40 MW 的光伏电场为研究对象,以2017 年1 月1 日至2018 年12 月31 日时间段内的NWP 数据和光伏功率实测数据为样本,时间分辨率均为15 min。其中NWP 为日前一天的预报值,2017 年数据为训练样本,2018 年数据为测试样本,用以验证数据预测的有效性。根据3.1 节的光伏功率组合预测模型具体步骤完成案例分析。
4.1 光伏功率非晴模型波动过程识别及分解
基于2.1 节所提的气象因素与功率波动过程匹配的天气分型方法,对2017—2018 年的NWP 数据及光伏功率数据按照晴天模型、多云模型、阴天模型、阵雨模型、全雨模型进行划分。各个模型所对应的划分天数见附录C 表C1。由表C1 可知,根据光伏功率波动特征筛选方法处理后的训练样本,筛选比例为13.42%,其样本量符合深度学习模型的需求。
4.2 光伏功率预测的关键气象因素确定
本文对2017—2018 年的晴天模型下的光伏功率与NWP 晴天相关因子、各天气分型下的功率波动过程与NWP 各波动相关因子进行了Granger 因果关系分析,分析结果见附录C 表C2—表C3。
本文选取置信度高于0.99 的NWP 因子作为波动模型的相关因子,以同样的方式对其他波动模型及晴天模型做Granger 因果关系分析,从而得出各自模型的NWP 相关因子,天气分型下各模型的NWP 相关因子统计结果见附录C 表C4。表中的NWP 相关因子按照置信水平排序,处于同一置信水平的NWP 相关因子被认为与光伏功率有同等的因果关系。
4.3 光伏功率短期预测准确性分析
在做好数据准备后,根据第3 章所述的组合预测模型进行预测。将2017 年的晴天模型与类晴空模型下的光伏功率值及其所对应的NWP 相关因子作为LSTM 模型的训练集,将2018 年所对应的光伏功率值作为测试集。LSTM 模型的网络结构主要包含2 个隐藏层,每个隐藏层分别有64 和128 个神经元。
图6 为晴天模型与其他天气分型下的类晴空过程预测结果对比图。图中选取的是2018 年6 月各天气类型下典型日的类晴空波动过程预测结果。

图6 各天气分型下光伏功率类晴空过程预测结果对比Fig.6 Comparison of forecasting results of photovoltaic power clear-sky-like process with different weather types
由图6 可知,晴天模型的光伏功率输出值较大,非晴模型下的光伏功率输出值较小,因此类晴空过程的预测精度主要在于NWP 晴天相关因子与光伏功率日输出最大值之间的映射关系是否准确。LSTM 模型擅长对时序数列的学习,因此可以比较准确地学习二者之间的映射关系。
同理,将2017 年的非晴模型下的光伏功率波动过程及其所对应的NWP 相关因子作为CNN 的训练集,将2018 年所对应的光伏功率值作为测试集。图7 为2018 年6 月各非晴模型下的光伏功率波动过程预测结果对比图。图中选取的是与类晴空过程展示结果中相同典型日下的非晴模型波动过程预测结果。
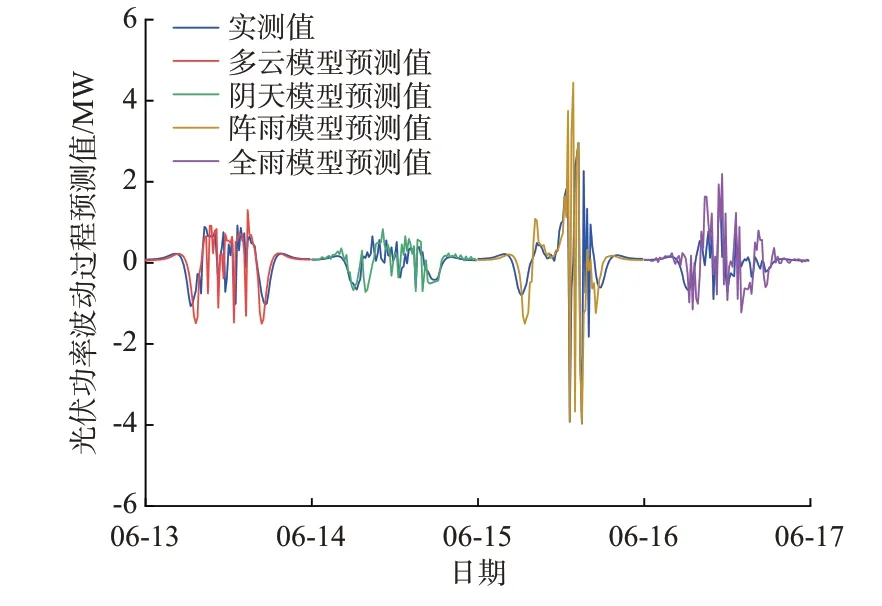
图7 非晴模型下的光伏功率波动过程预测结果对比Fig.7 Comparison of forecasting results of photovoltaic power fluctuation process with non-clear-sky model
由图7 可以看出,非晴模型下的光伏功率波动过程预测精度低于光伏功率类晴空过程,这就进一步表明了光伏功率预测精度主要取决于波动过程的预测精度。天气分型后,各训练样本的波动过程相似度提升,CNN 作为图像识别的常用算法之一,对波动过程的特征预测具有很好的表现。
将LSTM 模型所预测的类晴空过程与CNN 所预测的功率波动过程叠加即为最终预测值。为了验证本文所提预测方法的有效性,分别考虑晴天、多云天、阴天、阵雨天和全雨天5 种不同天气类型情况,对比以下4 种预测方法的效果。
方法1:采用本文所提出的基于天气分型的短期光伏功率组合预测模型。
方法2:采用本文所提出的天气分型方法及NWP 相关因子筛选方法,构建CNN 单体预测模型。
方法3:采用本文所提出的天气分型方法及NWP 相关因子筛选方法,构建LSTM 单体预测模型。
方法4:采用基于NWP 的天气分型方法及NWP 相关因子筛选方法,建立CNN-LSTM 组合预测模型。
方法2 和3 分别对CNN、LSTM 单体模型进行测试,从而分析2 种模型的预测特点;方法4 没有采用基于四分位法的光伏功率波动过程划分方法,即没有对5 种天气分型模型中的异常值进行筛选,以测试训练集数据质量对预测精度的影响。基于2018 年5 月的数据,4 种方法的预测结果与实际值的对比如图8 所示。

图8 不同预测模型下光伏功率预测值与实际值的对比Fig.8 Comparison of photovoltaic power forecasting value and actual value with different forecasting models
由图8 可以看出,分别采用CNN、LSTM 单体模型的方法2 和方法3 未能对光伏功率低频分量的波动幅值及高频分量的波动特征进行精确预测;未采用四分位法剔除异常数据的方法4 的预测结果中,由于各天气分型中训练集的光伏功率波动特征不统一,导致预测结果相较于本文模型有较大偏差。本文所提的组合预测模型有效地提升了预测精度,提升了模型的泛化能力。
根据3.2 节所述预测误差评价公式,对4 种方法进行误差比较,误差统计的样本量为2018 年全年数据,误差统计见表2。
由表2 可知,本文所提组合模型下的预测精度较其他3 种方法有所提高,尤其是对非晴模型的预测误差明显降低。可以看出,根据天气分型、异常值剔除及功率分解后的样本特征更加集中,深度学习模型的准确率有明显上升。方法2 所采用的CNN单体模型对非晴模型的预测精度明显高于LSTM单体模型。方法3 所采用的LSTM 单体模型对于晴天模型的预测精度有着明显优势。方法4 未使用四分位法剔除异常数据,可以看出相较于本文算法,其误差有明显升高,甚至在晴天模型下比方法3 所采用的LSTM 单体模型的预测误差要高。因此保证训练集的数据质量对于深度学习模型的预测精度提升有重要意义。根据预测误差精度的分析,进一步说明了本文所提出的组合预测算法的合理性。

表2 各天气模型下预测误差指标对比Table 2 Comparison of forecasting error indicators with different weather models
5 结语
本文基于NWP 分型因子将天气类型划分为晴天模型与非晴模型两大类,对非晴模型下的光伏功率分解为波动过程和类晴空过程,建立了针对各天气分型下波动过程和类晴空过程的组合预测模型。得到如下结论。
1)本文定义了功率波动过程的特征参数,提出了不同天气类型下功率波动过程判别式,对基于气象学知识所划分模型对应的功率特征进行特异性分析,剔除了由于NWP 精度所导致的问题样本,提升了样本质量。
2)本文基于VMD 算法,按照避免模态混叠及低频分量频率最低的原则,将光伏功率分解为波动过程和类晴空过程,为预测模型奠定了数据基础。
3)基于Granger 因果关系分析,筛选出各天气分型模型下所对应的NWP 相关因子,既减少了样本量,又提高了预测精度。
4)针对类晴空过程和波动过程的数据特征,结合机器学习算法自身的适应性条件,提出了CNNLSTM 组合预测算法,实现了基于NWP 相关因子,以光伏功率日波动过程为输入、以光伏功率日波动过程为输出的波动预测,显著提升了预测精度。
本文所采用的组合预测算法特异性不够强,在针对不同天气类型下建立具有明显特异性的预测算法方面还有进一步研究空间;此外,在探究光伏功率波动参数与NWP 相关因子之间的关联性还有研究空间。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

