ARIMA乘积季节模型与GRNN模型在猩红热发病预测中的比较*
潍坊医学院公共卫生学院(261053) 冯佳宁 肖宇飞 王晓璇 孙 娜 许小珊 王素珍 石福艳
【提 要】 目的 探寻适合猩红热发病的预测模型,为猩红热的预防和控制提供科学依据。方法 利用全国2011年1月至2018年12月的猩红热月发病率,通过R 3.6.1软件建立求和自回归移动平均(autoregressive integrated moving average,ARIMA)乘积季节模型和软件Matlab 9.1创建广义回归神经网络(generalized regression neural netword,GRNN),通过R2比较模型的拟合效果,平均相对误差比较模型预测能力,并对2019年1月-6月发病率进行预测。结果 创建的ARIMA(2,1,2)(0,1,1)12乘积季节模型平稳R2为0.336,预测2019年1-6月的发病率(1/10万)分别为0.637、0.274、0.377、0.579、0.910和0.937,GRNN模型的R2为0.823,预测2019年1-6月发病率(1/10万)分别为0.626、0.178、0.321、0.445、0.789和0.774。模型的平均相对误差分别为31.1%和20.3%。结论 ARIMA模型和GRNN模型均能对猩红热发病率进行预测,但GRNN模型预测能力较前者更优。
猩红热是儿童常见的急性呼吸道传染病,在我国属于法定报告的乙类传染病[1]。在对猩红热的发生、流行及其变化趋势进行预测时,通常采用求和自回归移动平均(autoregressive integrated moving average,ARIMA)模型[2-4],但是传染病的相关数据往往是不稳定的,易受自然和社会因素的影响而发生不同的变化,这类数据通常具有线性趋势和非线性关系,只通过线性模型信息提取不够充分。人工神经网络(artificial neural network,ANN)以其独特的并行结构、自适应、自组织、较强的容错性、稳健性等特点和独特的信息处理方法,在时间序列预测领域得到了广泛的应用[5-6]。目前在预测上应用较多的BP神经网络模型,在训练时存在收敛速度慢和容易出现局部最优解的缺点。而广义回归神经网络(generalized regression neural network,GRNN)基于径向基神经元和线性神经元建立,对样本数据要求不高,也可以有很好的预测效果,尤其对非线性问题处理效果较好。
本研究采用我国2011年1月至2018年12月的猩红热月发病率进行分析,分别建立ARIMA乘积季节模型和GRNN模型,并对两种模型的预测效果进行比较,从而为猩红热发病预警提供更优模型,在今后的预防决策中提供科学指导。
资料与方法
1.猩红热发病资料
本研究资料为中国疾病预防控制中心(http://www.chinacdc.cn/)报告系统发布的2011年1月至2018年12月猩红热月发病人数,计算发病率所用的人口数来自中国统计年鉴。
2.模型原理与方法
(1)ARIMA模型建立
ARIMA 模型是由美国统计学家Box和英国统计学家Jenkins提出的,ARIMA(p,d,q)模型中p,d,q分别表示自回归阶数、差分阶数、平均移动阶数[7]。ARIMA 模型记作:
(2)GRNN模型建立
GRNN是一种前馈式神经网络模型,是在观测样本中得到自变量与因变量的联合概率密度函数后,直接计算因变量对自变量的回归值[10]。GRNN 只需要人工调节光滑因子这一个参数,所以其结构的搭建比其他网络简单。其结构如图1所示,包括输入层、模式层、求和层与输出层等4层神经元。对应网络输入X=[x1,x2,…,xn]T,其输出为Y=[y1,y2,…ym]T。
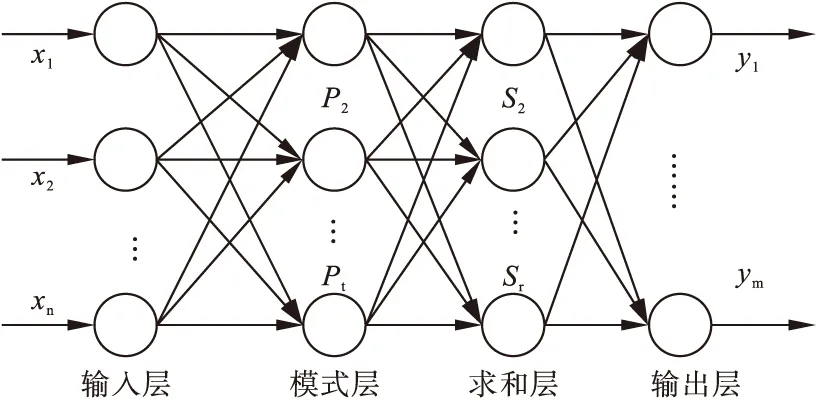
图1 广义回归神经网络结构图
GRNN模型建立可简单分为两步:①确定神经网络的输入和输出数据、训练样本和预测样本。本研究选择的输入数据为2011年至2017年猩红热月发病率,输出数据为2013年至2018年猩红热月发病率,训练样本选择2017年和2018年的1-6月发病率,对2019年1-6月的发病率预测。②创建GRNN模型。模型创建通过MATLAB中程序代码net=grnn(P,T,spread)实现,其中P为输入样本,T为输出样本,spread为光滑因子。预测程序代码为y=sim(net,p),p表示预测集的输入数据,y表示预测结果。通过交叉验证法获得最优光滑因子spread,使函数的逼近误差最小[11]。选择2011年-2017年任意6个月的发病率作为测试集数据,最小均方误差MSE对应的spread即为最优光滑因子。模型的建立在Matlab 9.1软件中实现。两模型比较通过决定系数R2检验模型拟合优度,通过平均相对误差MRE比较预测效果。
结 果
1.猩红热流行特征
研究数据为2011年1月至2018年12月底全国猩红热的月发病率。猩红热的流行情况在时间上具有明显的季节规律,主要集中在每年的5~6月和11~12月,具体情况如图2所示。

图2 2011-2018年猩红热月发病率
2.ARIMA乘积季节模型建立
(1)模型识别
根据图3中差分后序列均值围绕零值波动,得出经过1阶12步差分后序列满足了平稳性,白噪声检验显示为非白噪声序列(表1),可以拟合ARIMA模型进一步提取信息。
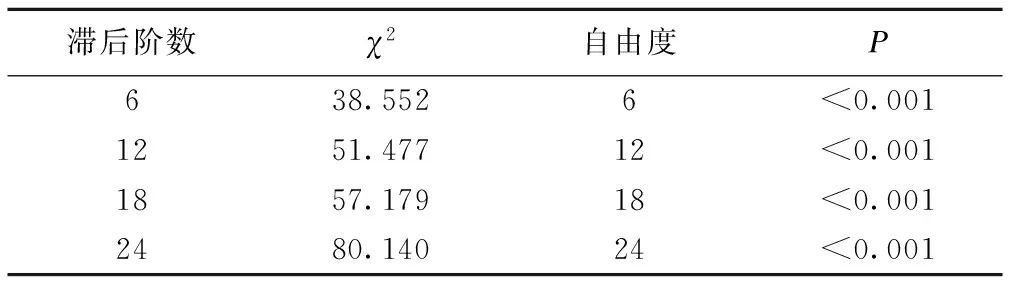
表1 差分后序列的白噪声检验

图3 1阶12步差分后序列的趋势和相关分析
首先观察差分后序列12阶以内的ACF和PACF的特征,存在短期相关性;考察延迟12阶的偏自相关系数,显示序列存在着季节相关,可以考虑建立模型ARIMA(p,d,q)(P,D,Q)s,根据ACF和PACF的特征拟合短期相关模型ARIMA(2,2)提取短期相关信息;季节信息的提取根据相关资料可知,一般季节模型阶数在2阶以内,拟对P、Q分别取值0、1、2以确定最佳模型。经过反复调整,根据AIC最小的原则,初步拟合模型ARIMA(2,1,2)(0,1,1)12,详见表2,图3。

表2 ARIMA(p,d,q)(P,D,Q)12模型的选取
(2)参数估计与模型检验
ARIMA(2,1,2)(0,1,1)12模型的各参数估计值检验均有统计学意义,见表3。且模型顺利通过了白噪声检验,见表4。由图4可知,拟合的模型的残差ACF与PACF均落在的2倍标准差范围之内,白噪声检验均在0.05之上,可认为模型拟合有效,模型的平稳R2为0.336。据此确定拟合的模型为:
根据建立的模型预测2019年1~6月的猩红热发病率(1/10万)的结果分别为0.637、0.274、0.377、0.579、0.910和0.937。
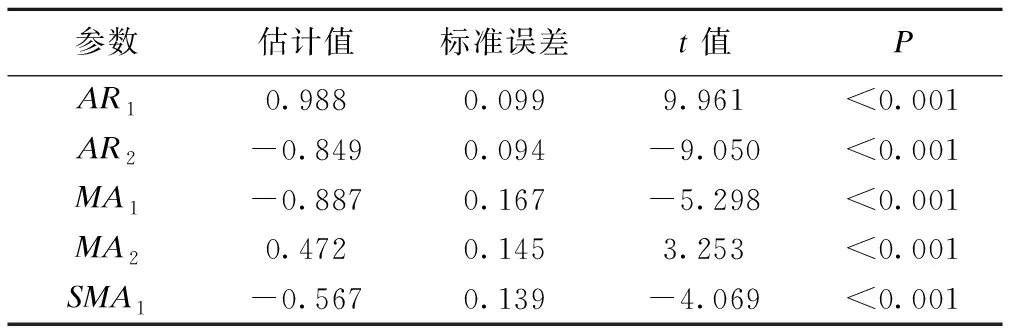
表3 ARIMA(2,1,2)(0,1,1)12模型参数估计
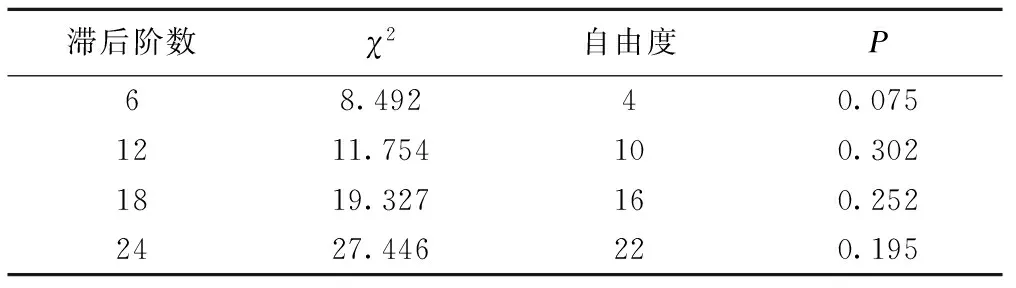
表4 ARIMA(2,1,2)(0,1,1)12模型残差白噪声检验
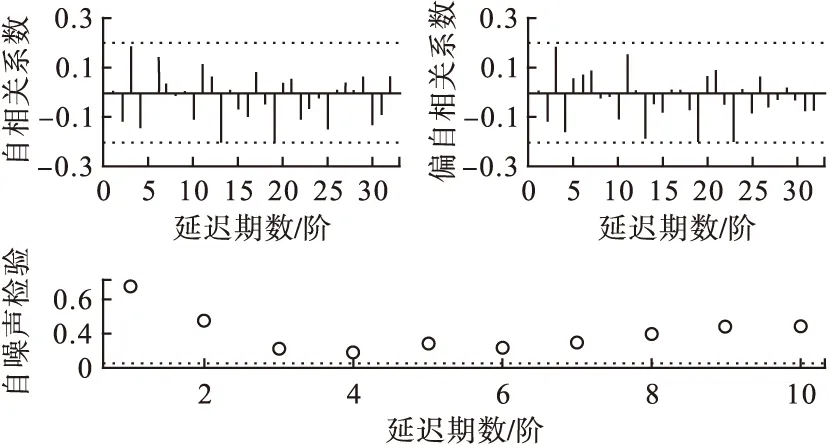
图4 ARIMA(2,1,2)(0,1,1)12模型的残差诊断
3.GRNN模型建立
本研究选择的训练集为2011年至2018年6月猩红热月发病率,测试集为2018年7~12月猩红热月发病率,模型的唯一参数spread由测试集最小均方误差MSE对应的最优值确定。可见图5,通过交叉验证寻找最优光滑因子,即当spread=0.05时,MSE最小,对应的MSE为0.011,逼近能力强;此时模型的R2为0.823,拟合效果较好。根据建立的GRNN模型预测2019年1~6月发病率(1/10万)分别为0.626、0.178、0.321、0.445、0.789和0.774。
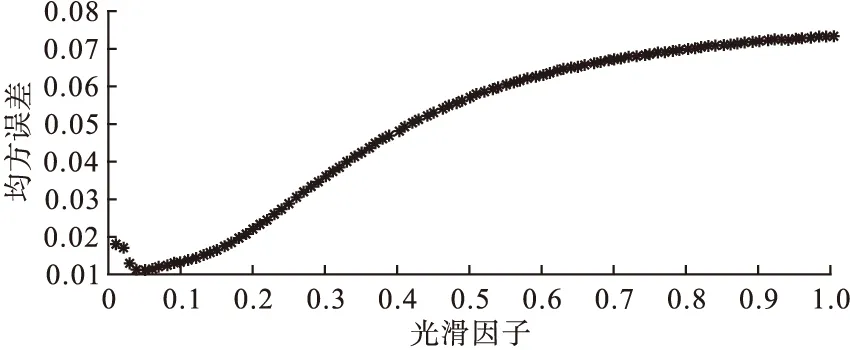
图5 光滑因子对应的均方误差曲线图
4.猩红热预测能力比较
分别通过对2011-2017年6月数据进行训练,预测2017年7~12月发病率;对2011-2017年数据进行训练,预测2018年1~6月发病率;2011-2018年6月数据进行训练,预测2018年7~12月发病率。两模型的预测能力通过比较平均相对误差大小,其中建立的三组GRNN模型的平均相对误差分别为23.0%、21.3%、16.8%以及总的平均相对误差为20.3%,三组ARIMA模型的平均相对误差分别为47.5%、25.0%、20.8%以及总的平均相对误差为31.1%,GRNN模型的平均相对误差均小于ARIMA模型,认为预测能力较后者更优。详见表5~7。

表5 ARIMA模型与GRNN模型第一次预测比较

表6 ARIMA模型与GRNN模型第二次预测比较
讨 论
众多研究表明ARIMA模型具有不受数据类型限制和较强适应性的优点,在短期预测中具有较好的表现能力[12-13]。ARIMA乘积季节模型可以提取出数据中蕴含的季节信息,当时间序列同时有短期相关性和季节趋势时,需要拟合ARIMA季节乘积模型以分析数据中的短期相关性、季节效应与随机误差的复杂关系。ARIMA模型作为一种较为经典的方法在传染病的预测上早已得到广泛的应用,并且表现出短期预测精度较高的优点。
人工神经网络能够逼近任意的非线性关系,具有良好的泛化能力,此外,人工神经网络没有任何对变量的假设要求,许多国内学者已将该模型应用在对疾病的发病率研究当中。GRNN模型其局部逼近能力强,且学习速度较快,既解决了局部最优问题,又同时提高了训练速度,且能保证预测的效果。
本研究结果显示,两种模型的预测结果与实际情况基本符合,均能较好地对全国猩红热发病率进行拟合。通过比较ARIMA乘积季节模型和GRNN模型的R2和预测结果的平均相对误差,GRNN模型均优于ARIMA乘积季节模型,由于猩红热受到气象因素、环境及个人防护等因素的影响,收集的资料数据是非线性的,而GRNN模型不对数据的分布做要求,故GRNN模型的预测能力更强,可以为今后研究猩红热等传染性疾病的流行趋势及提出防控措施提供科学依据。
本研究尚存在不足之处,GRNN训练样本的选取为猩红热的月发病率,神经网络的学习程度和预测能力可能会受到一定影响,且猩红热与气象因素密切相关,本研究未考虑气象因素也可能影响预测精度,且传染病流行规律复杂多变,在今后的研究中应及时更新数据对模型进行多次拟合,以提高预测水平。

