交叉滞后路径分析在变量因果时序关系研究中的应用*
周广帅 范冰冰 王春霞 游顶云 刘言训 薛付忠 陈 伟 张 涛△
【提 要】 目的 介绍交叉滞后路径分析原理及其在变量间因果时序关系研究中的应用。方法 交叉滞后路径分析模型基于交叉滞后面板设计,估计的路径系数具有明确的时间顺序关系,满足因果推断中“因在前果在后”的时序性要求。利用健康随访数据构建体重指数(BMI)与血尿酸(UA)的交叉滞后路径分析模型,探索BMI和UA的因果时序关系。结果 调整混杂因素后,基线BMI到随访时UA的路径系数(ρ2=0.060,P<0.001)明显大于基线UA到随访时BMI的路径系数(ρ1=-0.009,P=0.056),且两系数间的差异具有统计学意义(ρ2>ρ1,P<0.001)。在时间顺序上BMI增加先于UA升高发生。结论 BMI增加可能是高尿酸血症的原因,交叉滞后路径分析模型可以有效的识别变量间的因果时序关系。
实际研究中,通常利用因果图(casual diagram)的方式直观地标识危险因素之间的相关或因果关系,从而清晰地表达混杂效应、中介效应等多种因果推断的关键概念[1]。如图1所示的因果图模型,X为解释变量,Y为反应变量,Z为另一个解释变量。虚线双箭头表示存在关联,实线箭头表示有因果关系[2]。若X→Z则为中介效应模型,反之为混杂效应。因此,确定X和Z之间的因果方向是区分混杂和中介的关键。

图1 混杂和中介的因果图模型示意图
交叉滞后路径分析(cross-lagged path analysis)是利用纵向队列中两个及以上的面板数据,探索两个变量间因果时序关系(temporal sequence)的一种统计分析方法[3]。贝叶斯网络可采用有向无环图表示因果网络,被广泛应用于因果机制的发现和因果推断中,但其通常是基于横断面数据。交叉滞后路径分析的优势是结合了交叉滞后面板设计(cross-lagged panel design),估计的路径系数具有明确的时间顺序关系,符合“因在前果在后”的因果推断原则,常用于变量间因果时序关系的研究[4-7]。
本文将介绍交叉滞后路径分析的基本原理和分析步骤,并通过体重指数(BMI)与血尿酸(UA)因果时序关系的研究实例介绍该方法的实际应用。
交叉滞后路径分析
交叉滞后路径分析在交叉滞后面板设计基础上,研究两变量间的因果时序关系,在数据上要求两个及以上的面板数据,其模型示意图如图2所示。假设任意两变量分别为X和Y,其基线水平分别为X1和Y1,随访水平分别为Xt和Yt。其中β1和β2为自相关系数(autoregressive coefficient),表示随访测量(Xt或Yt)与基线测量(X1或Y1)的自相关关系;r1为同步相关系数(synchronous coefficient),是基线X1与Y1的相关系数;ρ1和ρ2为cross-lagged路径系数(cross-lagged path coefficient)。需注意的是,交叉滞后路径分析模型中并不包含Xt→Yt和Yt→Xt的因果路径,即Xt和Yt之间不存在同步效应。否则,模型中需要估计的参数个数将超过已有的方差和协方差数量,模型将无法识别[8-9]。
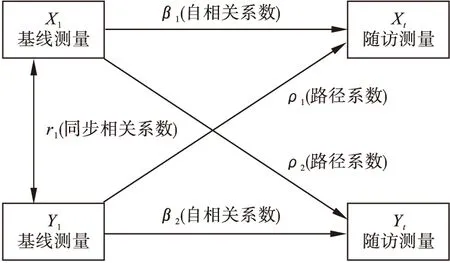
图2 交叉滞后路径分析模型示意图
在路径分析框架下,交叉滞后路径分析模型的形式如下:
Xt=α1+β1X1+ρ1Y1+e1
Yt=α2+β2Y1+ρ2X1+e2
其中α1和α2为模型截距,e1和e2为模型残差。
路径系数ρ是交叉滞后路径分析进行因果时序关系推断的依据,其含义为:在控制了因变量基线状态(如Y1)后,自变量(如X1)基线测量结果对因变量(如Yt)的影响,即Yt=α2+β2Y1+ρ2X1+e2。该模型经转换可表示为Y的动态变化同基线X1和Y1的回归形式,即ΔY=(Yt-Y1)=α2+(β2-1)Y1+ρ2X1+e2。计算的路径系数ρ在时间上具有明确的先后顺序(X1→Yt,Y1→Xt)。
通过路径系数ρ1和ρ2的比较可以确定变量间的因果时序关系,包含以下四种情况:若ρ1=0,ρ2=0,则X,Y间无因果时序关系;若ρ1≠0,ρ2=0,且两系数差异显著,则两变量为Y→X的单向因果时序关系;若ρ1=0,ρ2≠0,且两系数差异显著,则两变量为X→Y的单向因果时序关系;若ρ1≠0,ρ2≠0,则X,Y为相互调控的双向因果时序关系,此时若ρ1>ρ2且两者差异显著,可进一步确定主要因果时序效应为Y→X,反之则为X→Y。
研究实例
肥胖和高尿酸血症是心脑血管疾病的危险因素,大量流行病学和临床研究发现肥胖和高尿酸血症存在显著的相关性,然而其因果时序关系仍然存在争议。通常认为体重指数(BMI)增加会导致高尿酸血症,但也有研究发现血尿酸(UA)水平高的人群更易患有肥胖[10-12]。此外,基础研究表明尿酸可引起细胞内脂肪累积,导致体重增加[13]。本文将通过交叉滞后路径分析探讨BMI和UA之间的因果时序关系。
本研究基于山东某三甲医院2004到2015年的健康随访数据,选取基线年龄≥20岁,体检记录中包含两次及以上BMI和UA测量的体检参与者。由于数据中不包含高尿酸血症的相关治疗信息,为防止服药对尿酸水平的影响,排除了患有高尿酸血症的人群。本研究最终共纳入15348名对象,选取其基线和最后一次随访数据进行交叉滞后路径分析。研究对象的基线与随访特征如表1所示,其中男性9578人,女性5770人,基线平均年龄为39.68岁,平均随访时间为3.36年。
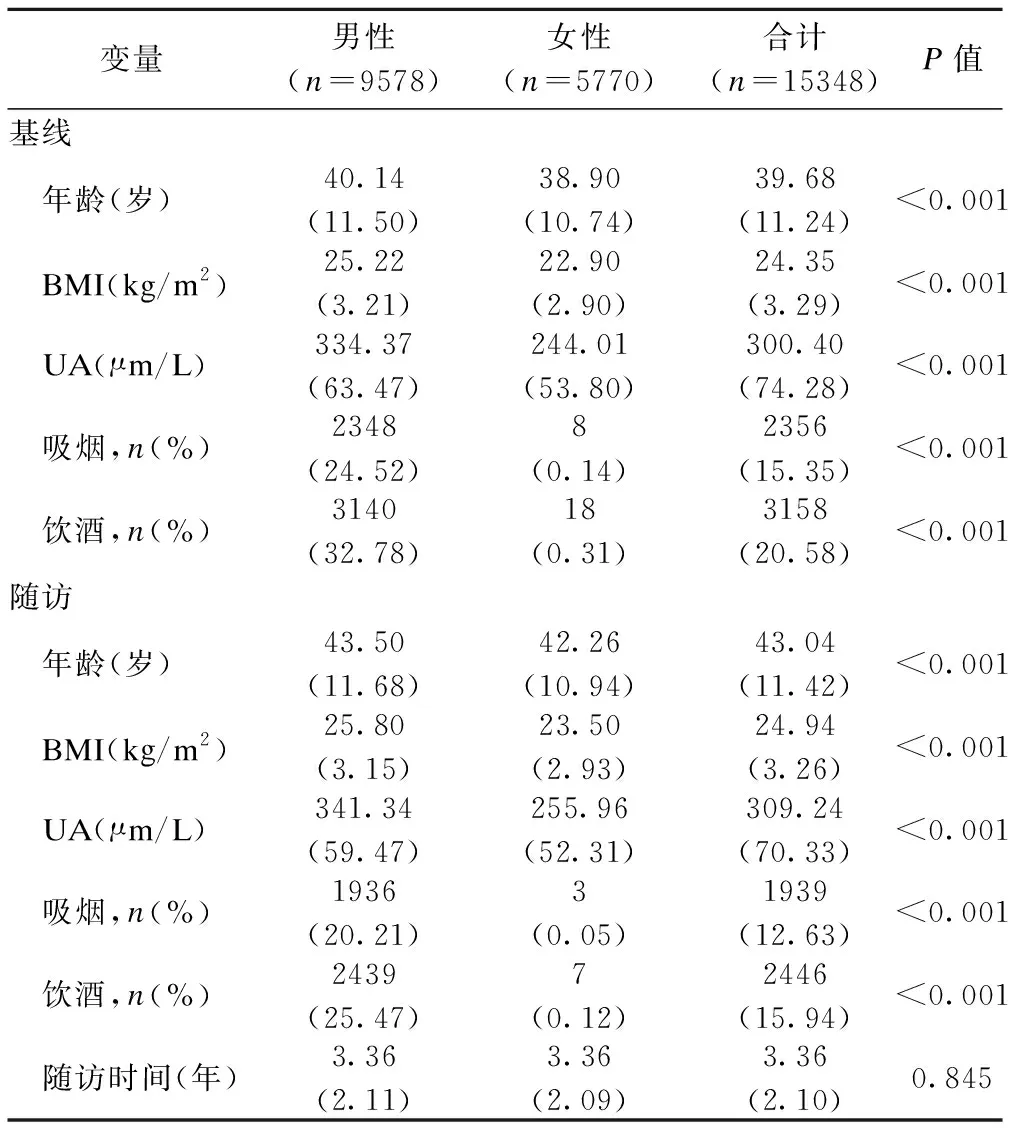
表1 研究队列特征
交叉滞后路径分析的建模步骤
交叉滞后路径分析作为路径分析的一种,可使用结构方程模型的分析软件建立模型,如:LISREL、AMOS、SAS中CALIS过程步、R中sem包、lavaan包等。
1.数据预处理
交叉滞后路径分析前,为控制潜在的混杂效应和消除量纲影响,需对研究变量进行回归残差分析,具体步骤为:(1)构建研究变量与混杂因素(如:年龄、性别、吸烟、饮酒、随访时间等)的多元回归方程;(2)对上述方程取残差,并进行Z转化的标准化处理。
2.计算协方差矩阵
结构方程模型又称协方差结构模型,其分析软件多以协方差矩阵为基础开始模型拟合,如LISREL,sem包等。此外一些结构方程模型分析软件也可以直接使用原始数据进行模型分析,如:AMOS、CALIS过程步、lavaan包等。交叉滞后路径分析模型在预处理时已将研究变量标准化,其协方差矩阵与相关系数矩阵相同。
3.模型构建
(1)根据现有研究确定各时点BMI与UA间的路径方向,建立如图3所示的交叉滞后路径分析模型,其结构方程组如下:
BMIt=β1BMI1+ρ1UA1+e1
UAt=β2UA1+ρ2BMI1+e2
上述方程组中基线BMI1、基线UA1、随访BMIt、随访UAt的协方差矩阵为[14]:
∑=
其中r1为基线BMI、基线UA的同步相关系数;re为e1、e2的相关系数。
(2)通过结构方程模型分析软件对上述模型进行参数估计。本研究采用lavaan包直接对原始数据进行模型分析。具体代码如下,#号后文字是对代码的注释:
install.packages(“lavaan”)#安装lavaan包
library(lavaan)#载入lavaan包
model1<-"BMIt~a1*BMI1+b1*UA1,
UAt~a2*UA1+b2*BMI1,
BMI1~~r1*UA1,
BMIt~~0*UAt"#输入模型公式
result<-sem(model=model1,data=usedata)#模型求解
summary(result)#查看模型结果
fitMeasures(result,c(“rmr”,“cfi”))#查看模型拟合情况
其中r1对应同步相关系数r1,a1、a2分别对应自相关系数β1和β2,b1、b2分别对应路径系数ρ1和ρ2;使用sem函数进行求解,model为需要输入的模型结构,data为分析所用的数据,此处usedata已经过预处理控制了混杂因素的影响;使用summary查看上述分析结果,使用fitMeasures查看模型拟合情况。
Lavaan包中默认使用极大似然法(maximum likelihood,ML)进行参数估计。其原理为通过迭代计算使模型隐含的协方差矩阵即“再生矩阵”与样本协方差矩阵间“距离”最小,得到模型最优解。ML属于完全信息方法,具有无偏、一致、尺度不变和渐进有效性的优点,是当前结构方程模型最常用的参数估计方法,其假设为变量服从多元正态分布[14]。
(3)判断模型参数估计是否合理,并通过拟合指数评价模型拟合情况。
常用的模型拟合指数有CFI(comparative fit index)和RMR(root mean-square residual)。其中CFI反映当前假定模型与变量间相互独立的虚模型(最不理想模型)的差异程度,具有不易受样本量影响,小样本时表现良好的优点,其值越大拟合越好;RMR则是基于假定模型整体残差的模型拟合指数,具有对误设模型较为敏感的优点,其值越小拟合越好。当CFI>0.90且RMR<0.05时表示模型拟合良好[4,15]。
(4)通过Fisher Z′ test对路径系数进行比较,确定主要因果时序效应。
实例分析结果
调整年龄、性别、吸烟、饮酒、随访时间后,BMI和UA在基线与随访时的相关系数和散点图如图4所示,其中基线UA与随访UA的相关系数为0.615,基线BMI与基线UA、随访BMI的相关系数分别为0.246、0.831,图中所有的相关系数均具有统计学意义。

图3 BMI与UA的交叉滞后路径分析模型
BMI与UA的交叉滞后路径分析模型结果如图3所示,调整年龄、性别、吸烟、饮酒、随访时间后,由基线BMI到随访UA的路径系数ρ2(ρ2=0.060,P<0.001)明显大于由基线UA到随访BMI的路径系数ρ1(ρ1=-0.009,P=0.056),且两系数间差异具有统计学意义(ρ2>ρ1,P<0.001)。BMI和UA两次测量间的自相关系数分别为0.834和0.600。模型拟合指数CFI和RMR分别为0.979和0.027,提示当前模型拟合良好。
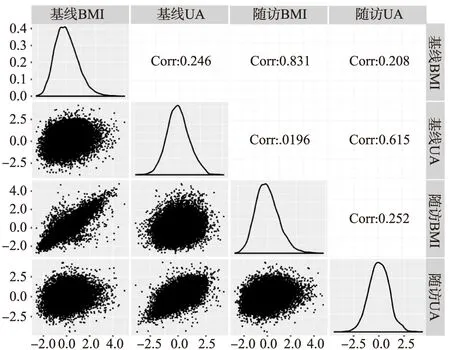
图4 基线与随访的BMI、UA相关系数和散点图
如图5所示,调整年龄、性别、吸烟、饮酒后,随着基线BMI四分位数的增加UA的年变化率逐渐升高,且增长趋势具有统计学意义;而随着基线UA四分位数的增加BMI的年变化率基本保持不变,增长趋势没有统计学意义。图5结果与图3中交叉滞后路径分析结果一致。

图5 不同基线四分位数下UA、BMI的年变化率
此外,本文选取随访队列中体检三次及以上的4797名参与者的随访信息,构建了三断面交叉滞后路径分析模型,进行了敏感性分析。模型结果如图6所示,调整混杂因素后,在不同断面间均存在的单向因果时序关系(ρ2=0.046,P<0.001;ρ4=0.061,P<0.001),与图3两断面模型结果一致。CFI=0.931,RMR=0.052提示当前模型拟合良好。综上,可以认为BMI与UA间因果时序方向为BMI→UA,即在时间顺序上BMI增加先于UA水平升高发生,BMI增加可能是导致高尿酸血症的原因。
讨 论
变量间的时序关系是流行病学中进行因果推断的重要原则之一,也是因果图模型中确定节点间箭头方向的基础。交叉滞后路径分析是利用纵向队列中两个及以上面板数据,探索两变量间因果时序关系的方法,其估计的路径系数具有明确的时间顺序关系,符合“因在前果在后”的因果推断原则,为进一步的因果关系探索提供了依据。
交叉滞后路径分析需满足以下假设:(1)变量服从多元正态分布,当违背正态性假定时,使用ML法的模型参数标准误将被低估,增大I型错误风险,此时可通过变量转换,或者通过S-B调整的ML法、渐进自由分布法、自助抽样法等进行模型拟合[14];(2)人群内部一致性,交叉滞后路径分析关注总体层面的平均因果效应,未充分考虑个体间差异,当研究变量个体变异较大时可能影响模型结果[16];(3)随访间隔接近真实因果效应时间,变量间的相互作用常需一定发生时间,如果随访间隔太短或太长,因果效应可能尚未发生或已经消失,影响时序关系判断,模型选取的随访间隔应尽量接近真实的因果效应时间,但实际应用中受限于现有数据,该假设往往容易被违背[17]。此外需注意的是交叉滞后路径分析仍借助常规回归方法控制混杂效应,模型结果可能受到未知混杂影响。另一方面,交叉滞后路径分析属于验证性分析,模型假定的因果方向均应来自现有人群或理论研究。
两变量两断面交叉滞后路径分析是该模型最基本的形式,当包含三个或者更多面板时,可构建包含多个随访间隔的交叉滞后路径分析模型,通过比较各随访期内的路径系数,探索不同时点下变量间因果时序方向和强度的变化规律[18]。多断面模型中,每个面板的随访人群均应处于相同年龄段或生命历程阶段(如:儿童发育阶段、女性绝经状态等)。其中三断面模型要求三个随访断面均处于相同生命历程阶段(如:均为成年期),常用于两断面模型的敏感性分析,以检验随访间隔改变对模型结果的影响。本文实例分析部分BMI与UA的三断面交叉滞后路径分析模型与两断面模型结果一致,均提示BMI增加是导致高尿酸血症的原因。多断面模型的模型构建和求解过程与两断面模型类似,鉴于文章篇幅不再展开。此外,随着模型发展交叉滞后路径分析已衍生多种模型形式,关注较多的有RI-CLPM(random-intercept cross-lagged panel analysis model)、ALT-SD(autoregressive latent trajectory model with structured residuals)等,前者通过在模型中引入截距因子(潜变量),为控制个体间差异对变量间真实时序关系的影响提供了可能[16];后者则将交叉滞后路径分析与潜变量增长曲线模型结合,使模型在估计变量间因果时序关系的同时也可获得变量的总体变化轨迹,扩展了交叉滞后路径分析模型的应用范围[19]。

