几何直观在解决问题教学中的运用

周纯

借助几何直观可以把复杂的数学问题变得简单、明了，有利于探索解决问题的思路。通过一线教学得知：不管是在低年级的实物图，还是中高年级的线段图和示意图，对于描述数学问题、剖析数量关系、探索解决问题策略对学生来说都可以起到积极的作用，均可以更有效地提高学生分析问题、解决问题的能力。

一、借助几何直观，描述数学问题

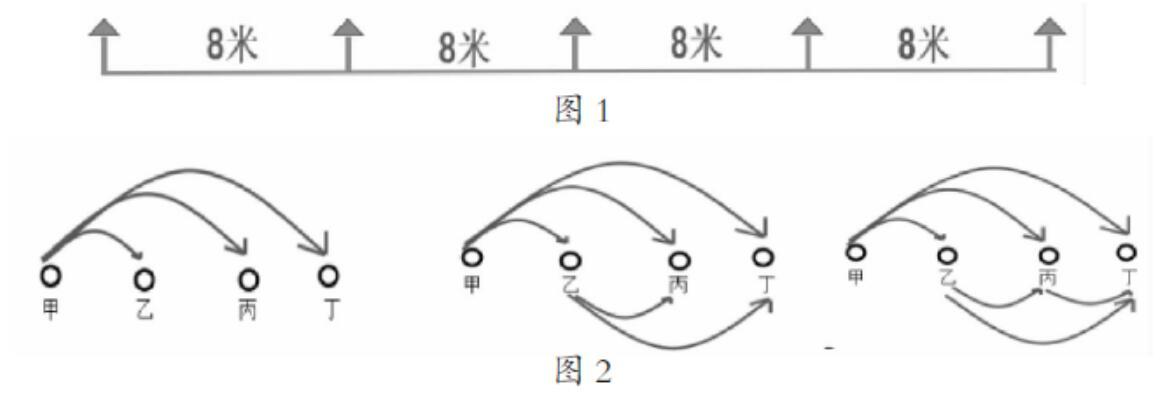
借助几何直观来描述数学问题，首先要了解题目讲了一件什么事情，充分理解题目意思，进而剖析题目中蕴含的数量关系，以达到从抽象到形象化的思维转换。例如：教学三年级的植树问题时有一道这样的题目：“某社区为了提高绿化率，在一条路的每边每隔8米种一棵木棉花树，各边种了5棵。从第一棵木棉花树至最后一棵木棉花树的距离是多少米？”这样关于生活中的数学问题，对于中年级的小学生来说，绝大部分学生可以直接列出算式“8×5=40（米）”，即便指出错误，告诉学生要先用“5-1=4，再用8×4=32（米）”才是正确的，有个别孩子还不能完全理解题目中所表达的含义。这时，老师让学生画出简单的直观符号，这样学生会较快地弄懂题目意思。接着教师利用希沃白板通过演示，再引导学生看图1说出题目意思：各边种了5棵树，其实就是求每边的4个间隔，每隔8米种一棵木棉花树，要计算从第一棵木棉花树到最后一棵木棉花树的距离就是要算4个间隔的长度。学生们根据直观图形来口头描述，把抽象的数学问题变得更加直观化、形象化，从而达到提高学生解决问题能力之效。

二、应用几何直观，理解数量关系

在实际教学中，教师可以适时提醒并鼓励孩子们动手画一画，实质上将较为抽象复杂的生活数学问题转换成直观形象的简单图形问题，用更形象、直观、有效的方式去分析题目中的數量关系，找到已知信息和未知信息的关联，从而实现语言文字信息与直观图形信息之间的转换，也就是抽象信息与直观信息之间的转化，达到顺利解决问题之效。数学教学活动是让学生有计划、有目的地去认知练习题中确定的对象，明确的目的性，促进感官的集中指向，感知目标越鲜明，建立的表象就越清晰。直观性极强的线段图，可以为学生提供有利的感觉和认知，使学生通过直观观察寻找数学信息，分析并把握数量关系，从而揭示反映问题的本质。

三、凭借几何直观，探索解题策略

在数学教学活动中，凭借几何直观的特点，通过对直观图形的观察和动手操作的学习活动，可以同时取得和储存不同的表象，更能帮助学生逐步提升能力。如三年级下册“数学广角——搭配”中有一道这样的题目，学校选拔学生参加区的乒乓球比赛，共有4个孩子报名参加预赛，其中每2个孩子进行一场比赛，一共要进行比赛多少场？”对于这样的比赛问题，孩子们用枚举的方法一一罗列出来4个孩子互打比赛的情况，这时教师可以引导学生用4个圆圈表示4个孩子，每两个圆圈间的线段来表示打乒乓球比赛，就可以画出图形。

从图2中可以看出，每一个孩子都可以和其他3个孩子打球比赛，那么4个孩子一共有12场比赛，但是由于“每2个孩子进行一场比赛”，因此每进行2场比赛（如小王和小博进行小组比赛，小博和小王进行小组比赛）中有1场是重复，正确地结果是6场。同样还是这个图，教师还可以跟学生讲授第二种方法，第一个同学小王可以和小博、小江、小旭三个同学打比赛，即：小王-小博，小王-小江，小王-小旭，第二个同学小博已和小王打过比赛了，只要和小江、小旭两个同学打比赛，即：小博-小江，小博-小旭，同理，小江只要和小旭一个同学打比赛，即：小江-小旭。这样，一共需要打6场比赛。

在教学中借助几何直观和运用转化的数学方法，把生活问题转化成数学问题，用“四个圆圈（每三个圆圈不共线）一共可以连多少条线段”的问题来帮助学生寻找解题方法。

责任编辑    徐国坚