中学数学考试评卷中的概率问题探讨*

华南师范大学数学科学学院(510631) 葛文秀

广东食品药品职业学院软件学院(510665) 阮丽华

一、导言

有些关键考试的结果对于受试者而言,其重要性是不言而喻的,比如高考成绩甚至会影响到考生的一生.考试结束之后,接踵而至的是阅卷评分工作.随着现代科学技术的快速发展,阅卷方式也发生了较大的变化.在现代信息技术出现之前,阅卷的主要方式是手工阅卷.光学标记阅读机的出现, 完成了通过扫描信息卡上的涂写内容实现对选择题目的自动判读.随着网络通信技术的发展,网上阅卷开始被大量采用,大大节省了成绩的录入时间,提高了阅卷的工作效率[1].

然而,值得注意的是,网络阅卷只是阅卷方式的改变,由原来的纸质答卷变为电子扫描之后的电子内容,其非选择题部分仍然需要人工阅卷.同时,随着考试频率的增加,教师要在有限的时间内对大量的试卷给出科学、公平的评判仍然是一项重要而且艰巨的工作.已有少量文献开始探讨将人工智能技术引入到评卷工作中[1-4].不同于已有文献,本文将以地市级模拟考试为例探讨大型数学考试中将填空题目分割与否对考试评卷工作中的错判数量和工作效率的影响.此外,本文采用概率建模和随机模拟两种方法分析问题,也是对中学数学教育中有关概率统计内容的一个较好的应用范例.

二、两种评卷方式的比较

本文讨论中学数学大型模拟考试中关于4 道填空题目的两种评卷方式:

方案1将4 道填空题目切割,即阅卷系统每次向一位评卷员发送的任务是评阅一道题,以下简称为切割填空题;

方案24 道填空题目未切割,即阅卷系统每次向一位评卷员发送的任务是评阅4 道题,评卷员需将4 道题的成绩一起提交,以下简称为未切割填空题.

在具体讨论之前,首先介绍一下大型数学模拟考试填空题目的评卷制度.大型中学数学模拟考试填空题的改卷实行“二评制度”,即一份答卷首先由两名评卷员评分,称为第一评和第二评.若两名评卷员的给分完全一致,则此份试卷的给分确定.否则,此份试卷将提交到题组长处进行第三评.

本文主要研究两个问题:问题1.在两种方案下,由两名评卷员同时改错导致的错判试卷数量; 问题2.在两种方案下,组长卷的数量.

为表述方便,引入如下符号:N:考生试卷总份数;Ai:第i题两名评卷员同时改错,i=1,2,3,4;Bij:第i题第j名改卷员改错,i=1,2,3,4,j=1,2;Di:第i题两名评卷员的给分不同,i=1,2,3,4.同时做如下假设:每名评卷员每道题的改错概率相同,而且任意两名评卷员改错与否是相互独立的.

问题1.两种方案下,由两个评卷员同时改错导致的错判试卷数量

方案1.切割填空题.

记每名评卷员每道题目的改错概率为参数p1, 即P(Bi1)=P(Bi2)=p1.进而, 因为两名评卷员同时改错同一道题目而导致错判的概率P(Ai)=P(Bi1∩Bi2)=.因为填空题切割,则改卷数量由N份变成4N份.记Y1:4N份试卷中, 两名评卷员同时改错的数量.则Y1服从参数为4N和的二项分布Y1～B(4).

方案2.未切割填空题.

记每名评卷员每道题目的改错概率为参数p2, 即P(Bi1)=P(Bi2)=p2,i= 1,2,3,4.进而, 第i道题目两名评卷员同时改错的概率P(Ai)=P(Bi1∩Bi2)=.记X:同一份试卷两名评卷员同时改错的题目数量.则有X ～B(4).从而,对于一份试卷,此份试卷被两名评卷员同时改错导致错判的概率为

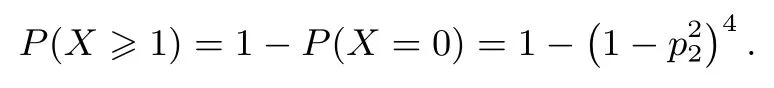
记Y2:N份试卷中,两名评卷员同时改错导致错判的数量.则有Y2～B(N,1-(1)4).

因为Y1,Y2的分布不同, 从期望角度进行比较, 可知:E(Y1)=4Np21,E(Y2)=N[1-(1-p22)4].当p22很小时,由Taylor 展开式可得,

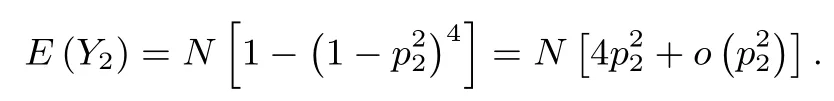
由上面的概率建模,不难发现:若p1=p2,从期望角度看,两种不同方案下,因为评卷员同时改错导致的错判试卷数量无显著差异.

表1 给出了在考生人数N= 400000,p1=p2=p分别为0.0001,0.0005,0.001,0.005 以及0.01 的情况下,两种方案平均错判的数量E(Y1),E(Y2)以及两者差值的模拟结果.

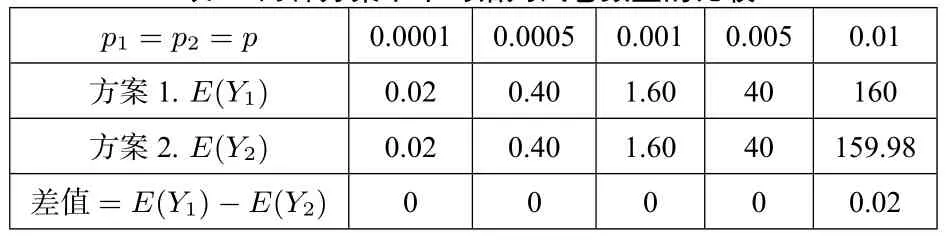
表1.两种方案下平均错判试卷数量的比较

注:结果保留2 位小数.

由上面的模拟结果发现,与理论结果相同,在每名评卷员每道题目的改错概率相同的情况下,由期望角度看,两种方案的平均错判数量没有显著差异.

问题2.在两种方案下,组长改卷量

因为填空题每道题目的给分只有正确和错误两种情况,按照改卷质量控制的要求,若两名评卷员对同一道题目的给分不一致,则此份试卷将由题组长批改.

方案1.切割填空题.

与问题1 相同,仍然记每名评卷员每道题目的改错概率为参数p1.则对于第i题,两名评卷员给分不一致的概率为

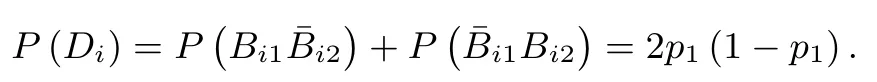
记Y3:4N份试卷中, 题组长的改卷数量.则有Y3～B(4N,2p1(1-p1)).

方案2.未切割填空题.

仍然记每名评卷员每道题目的改错概率为参数p2.则对于第i题,两名评卷员给分不一致的概率

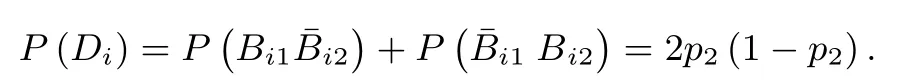
记Z:同一份试卷两名评卷员给分不一致的题目数量.则Z ～B(4,2p2(1-p2)).进而对于一份试卷,需要题组长批改的概率为

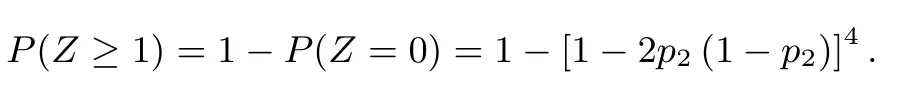
记Y4:N份试卷中,题组长的改卷数量.则Y4～B(N,1-[1-2p2(1-p2)]4).

因为Y3,Y4的分布不同, 从期望角度进行比较:E(Y3)=8Np1(1-p1),E(Y4)=N{1-[1-2p2(1-p2)]4}.

表2 给出了在考生人数N= 400000,p1=p2=p分别为0.0001,0.0005,0.001,0.005 以及0.01 的情况下,两种方案下组长卷的数量E(Y3),E(Y4)以及两者差值的模拟结果.

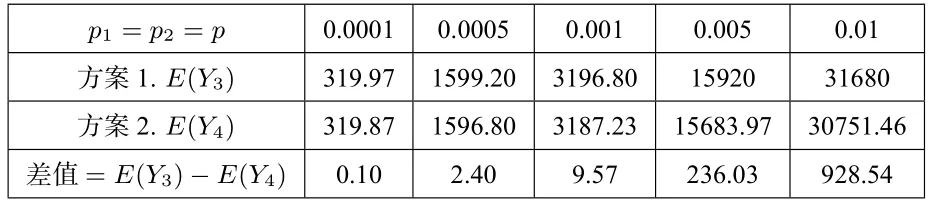
表2.两种改卷方案下组长卷数量的比较

注:结果保留2 位小数.

由上面的模拟结果不难发现:在两种方案下,若每道题目每个评卷员改错的概率相同,则从期望角度比较,因为两个评卷员给分不一致导致的题组长改卷数量方案1 比方案2 略多,而且随评卷员改错概率增加,两种方案的题组长改卷量差异增大.

三、结论

本文以中学数学大型模拟考试的填空题为例,探讨切割填空题的评卷方式与未切割填空题的评卷方式两种方案在试卷错判数量以及相应的组长卷数量方面的优劣比较.通过概率统计建模以及模拟研究发现:在两种方案下,从期望的角度出发,因为两名评卷员同时改错导致的错判试卷数量无显著性差异;同时,因为两名评卷员给分不一致导致的题组长改卷量切割填空题的方案1 比未切割方式的方案2 略多,而且随评卷员改错概率增加,两种方案的组长卷差异增大.

此外,相比于未切割填空题的方案2,切割填空的方案1每个题目的评分都需要点击“提交”按钮,导致评卷员点击鼠标次数高于方案2.同时,因为阅卷数量大,调用试卷过程中涉及到的网络延时也是一个影响方案1 工作效率的因素.然而,方案1 并不是完全没有优点.切割填空的方案1 将能够获得每一道填空题目的分值数据,有助于进一步分析处理.

综上所述,本文认为在保证公平性、科学性基础上,从提高大型模拟考试评卷的工作效率角度出发,基于错判试卷数量和组长卷数量两个指标,未切割填空题的方案2 优于切割填空题的方案1.