激波风洞7°尖锥边界层转捩实验研究

栗继伟，卢盼，2，汪球，2，*，赵伟，2

（1.中国科学院力学研究所 高温气体动力学国家重点实验室，北京100190；2.中国科学院大学 工程科学学院，北京100049）

边界层转捩是指边界层流动从层流发展到湍流的过程，是一个由多种因素耦合的非线性复杂流动物理现象。转捩问题是流体力学重要的基础研究课题之一，与湍流问题一起被称为“百年（或世纪）难题”。转捩问题在低速流方面已经有了一定的进展，但对于高超声速边界层转捩问题，低速流动的稳定性理论将不再适用，国内外学者在理论研究、数值模拟（DNS）、地面实验及飞行实验方面开展了大量研究工作，近年来虽然也有一些进展，但是仍存在严重的不足，相关研究具有重要的工程及学术价值［1-4］。

Mack［5］利用线性稳定性理论首先发现，在高超声速边界层中，除了T-S不稳定波外，还存在一族在壁面和边界层内来回反射的高频谐波，其中最不稳定的一个被称为Mack第二模态波。Mack第二模态与第一模态T-S波在高超声速边界转捩中都起到作用，但何种模式在转捩过程中起主导作用还没有统一认识［6］。目前，对高超声速转捩研究的手段主要有飞行试验、数值模拟及高超声速风洞地面实验。飞行试验来流为真实来流，其提供的转捩实验数据可作为转捩预测的基准数据。但飞行试验中实验条件存在诸多限制，如对试验高度大气来流扰动认识不足，试验传感器种类及测点位置选择有限，试验过程中飞行器烧蚀对表面流动状态如壁温、表面粗糙度等的影响［7］，这些限制条件使得对影响高超声速转捩因素的细致研究十分困难；同时飞行试验高昂的花费及试验模型的不可重复利用也使得现有的飞行试验数据十分有限。数值模拟近年来在高超声速边界层转捩的研究中取得了很大的进展［8-9］。但由于其计算量巨大，能模拟的实例有限，计算中初始扰动的引入有较大的人为影响因素，故其模拟通常为特定流场在特定扰动条件下的因素，在认识转捩过程中参数影响方面的能力仍显不足。

地面高超声速风洞能保证来流具有较好的重复性，易于实现各种来流及壁面条件下重复性的实验研究，是研究高超声速边界层转捩的主要地面实验手段，但高超声速转捩受来流扰动影响较大，Fedorov［10］指出随着初始扰动幅值的增加，转捩将经过截然不同的几种路径。由于目前对高超声速风洞流场的背景扰动认识十分有限，不同风洞的转捩结果也可能由于其背景扰动的不同呈现出较大的差异。背景噪声水平与飞行条件相当的静音风洞对转捩机理的深入认识具有重要作用，国内北京大学和国防科技大学的静音风洞已经建成并投入使用，并在静音风洞中开发出了多种转捩现象的测试技术［11-15］。但目前静音风洞喷管口径较小，来流雷诺数相对较低，在静音风洞中尖锥边界层转捩还难以发生，需要采用特殊措施如添加粗糙带或具有逆压梯度的裙锥模型进行实验。现有的风洞设备仍以常规激波风洞为主，在不同背景噪声的激波风洞中进行转捩实验能在依托现有的大量风洞实验数据基础上加深对高超声速边界层转捩的认识。

早期关于边界层不稳定性的实验主要用热线风速仪作为测量手段，但其只能针对低速、连续式风洞进行实验［16-17］。高超声速边界层内不稳定性发展会在物体表面加载较强的压力脉动，通过研究这种压力脉动的特性和发展规律有助于加深对转捩过程中物理机制的认识，同时对转捩位置的预测提供一定的理论依据。国内外已经开展了在高超声速风洞中测量高频脉动压力的工作［18-24］，这些实验观察到了高超声速边界层中第二模态波的产生与发展，表明用高频脉动压力传感器研究边界层转捩过程是可行的。另外，转捩过程中热流具有显著的提升，热流的测量一直是风洞实验中判断转捩位置的重要依据之一。天津大学韩健等利用薄膜电阻温度计在马赫数6的炮风洞上进行了5°尖锥的热流测量，对热流信号的小波分析揭示了转捩过程中热流扰动的分布特征，但受模型尺寸的限制并未观察到转捩结束位置［25-26］。ALTP（Atomic Layer Thermopile）高频热流传感器的脉动热流的测量结果也揭示了转捩过程中热流脉动度的增长，小波分析的结果也出现了与压力脉动类似的第二模态不稳定现象，揭示了第二模态不稳定波的波包特性［27-28］。虽然国内外在边界层转捩的实验研究方面已经取得了一定进展，对于高超声速边界层转捩的准确预测目前仍然没有统一的理论和计算方法，亟待更多的实验数据来分析其机理并建立转捩预测模型。

本文针对高超声速边界层转捩问题，在中国科学院力学研究所JF8A高超声速激波风洞中开展了7°半锥角的尖锥边界层转捩实验研究，利用响应频率达到1 MHz量级的高频压力传感器对风洞自由流及尖锥壁面脉动压力进行了测量，给出了风洞试验状态下的自由流噪声及尖锥模型表面扰动波的发展过程。本文研究结果能够为高超声速边界层转捩的数值及理论分析提供数据支撑。

1 实验设置

1.1 实验设备及实验状态

本文实验在中国科学院力学研究所JF8A高超声速激波风洞中进行，如图1所示，该激波风洞是一座中等规模的激波风洞，同时兼有激波风洞和炮风洞2种运行模式。风洞采用压缩空气作为驱动气源，通过更换喷管能够获得马赫数5～15的实验气流，风洞的喷管出口直径800 mm，试验段长度超过2 m，试验段后串接的真空舱容积超过100 m3，风洞单位雷诺数最高可达5×107/m，有效试验时间根据不同的实验状态约为5～30 ms。风洞能够开展气动模型的气动热/力测量、激波与激波、激波与边界层干扰等实验研究，由于风洞来流雷诺数范围较宽，对高超声速边界层转捩的实验具有一定的优势。

本文实验在JF8A激波风洞马赫数为6.5的喷管下开展，风洞具体状态参数如表1所示，P0为风洞驻室总压，H0为驻室总焓，T0为驻室总温，ρ∞为风洞自由来流密度，u∞为来流速度，T∞为来流静温，Ma为来流马赫数，Re为来流单位雷诺数。实验状态下的典型压力曲线如图2所示，包括驻室压力、皮托压力及球头驻点位置的PicoCoulomB（PCB）传感器信号，虽然压力平稳区域较长，本次试验中相关数据的处理只取图2中15.5～19.5 ms时刻，4 ms的有效数据能满足本文所有数据分析需求。

图1 JF8A高超声速激波风洞Fig.1 JF8A hypersonic shock tunnel

表1 风洞试验状态Table 1 Test conditions of wind tunnel

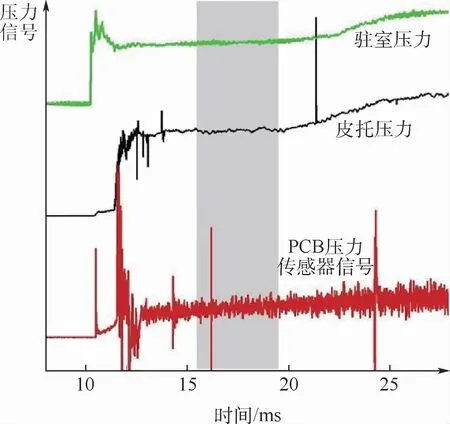
图2 试验典型压力曲线Fig.2 Typical pressure histories in test

1.2 实验模型

本文实验中选用的模型是半锥角为7°的尖锥，尖锥总长为1 100 mm，模型示意图如图3所示。

模型加工时保证表面光滑，无缝隙、无台阶。尖锥沿母线布置有传感器安装孔，分别安装薄膜电阻温度计测量热流及PCB压力传感器测量脉动压力。沿母线上共布置74个薄膜电阻温度计，以尖锥母线为x坐标，第一个传感器距离尖锥前缘245 mm，高密度布置的热流传感器能够捕捉尖锥壁面边界层从层流-转捩-湍流变化过程中的热流分布。实验中根据每车次的实验结果，对热流信号异常或者损坏的传感器进行更换，保证实验的重复性和准确性。另外，沿母线布置的PCB压力传感器数量为6个，其具体坐标依次为245、405、525、605、745和985 mm。

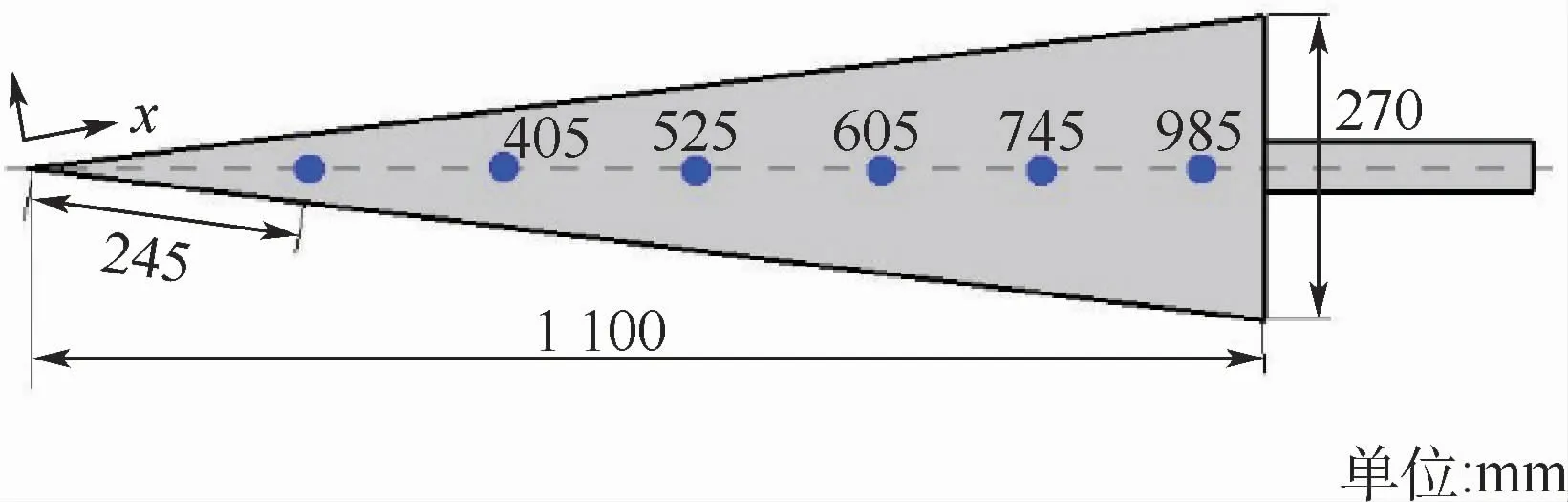
图3 尖锥模型及传感器安装示意图Fig.3 Schematic diagram of sensor installation on sharp cone model

1.3 测试传感器

1.3.1 测热传感器

实验中选用中国科学院力学研究所自行研制的铂薄膜电阻温度计，其响应较快，是专为短试验时间的脉冲型风洞热流测量而研制的。传感器制作时将铂通过真空溅射的方法溅射到玻璃表面，铂薄膜的厚度约为10-8～10-7m，两端选用银浆作为引线，玻璃棒直径2 mm，长度约为30 mm。铂薄膜电阻温度计输出的信号经低噪声放大器放大后由高速采集器采集并送入计算机储存、处理，采集频率为1 MHz，整个采集系统的精度为±0.5%。在传感器获取测点温度后，由Schultz和Jones的理论公式即可推算热流［29］：

1.3.2 脉动压力传感器

脉动压力的测量采用PCB132A31型的高频压力传感器，该类型压力传感器由于其自身交流耦合的特性，不适合用于平均压力绝对值大小的测量，但是对动态变化压力具有很高的响应频率。传感器的固有频率达到1 MHz以上，最小压力分辨率为7 Pa，传感器的灵敏度约为23 mV/kPa，实验中采样频率为3.5 MHz。

压力传感器有效试验时间内的典型信号曲线如图4所示，由于传感器的有效响应频率在11 kHz以上，因此本文在对压力信号进行处理时利用巴特沃斯滤波器对信号进行了11 k Hz的高通滤波，尖锥模型上第一个测点的原始信号、滤波信号及最后有效数据如图4所示，P′为脉动压力。滤波后的压力脉动约为±100 Pa，后续关于PCB数据的处理均是针对高通滤波后的数据进行处理和分析。

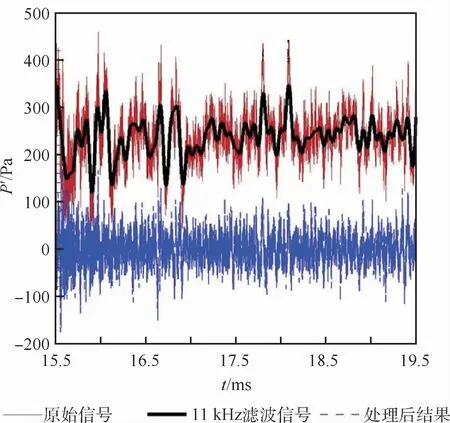
图4 原始及滤波后的PCB压力传感器信号Fig.4 Raw and filtered PCB pressure sensor signals

1.4 风洞噪声测量

风洞自由流噪声对转捩有重要的影响，其可能影响模型转捩的位置。为了尖锥模型数据的有效分析和应用，本文同时测量JF8A激波风洞的自由流的噪声，常用的风洞自由流噪声测量方法有热线风速仪、皮托压力测量、壁面压力测量，以此来推算自由流噪声，它们各有优缺点。目前通常采用PCB压力传感器测量皮托压力来推算自由流噪声，但是传感器直接受到高速气流的冲刷，敏感元件存在损坏的风险，本文在喷管中心区域及边界层内各安装一个PCB压力传感器，边界层内的传感器距离管壁为40 mm，同时采用常规压阻传感器测量皮托压力，皮托压力传感器型号为上海天沐公司的NS-3，其频响大于50 k Hz。自由流噪声定义为

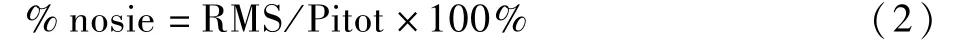
式中：RMS为有效实验时间内压力脉动的均方根值；Pitot为该段时间内皮托压力值，试验测量皮托压力值为28 kPa。根据式（2）计算获得本状态下风洞中心区域噪声为2.8%，边界层内的噪声为7.8%，核心区域内的噪声值和国内外其他激波风洞所给出的幅值相当［24］。

2 结果与讨论

2.1 尖锥壁面热流分布

为了补充分析PCB脉动压力信号，本文同时开展了尖锥模型气动热测量，通过热流变化来评估模型表面PCB压力传感器位置所处的流态。本文实验状态的尖锥热流曲线如图5所示，热流出现从层流到转捩的过程，转捩位置约为530 mm处；除实验结果外，同时还给出了求解边界层方程所获得的层流状态下的热流值，以及利用文献［30］中的计算公式所获得的尖锥在湍流状态下的热流值，试验值和理论解基本吻合。

2.2 高频脉动度

图6给出了6个PCB压力传感器的原始脉动压力信号，当来流作用在传感器表面时，压力有一个阶跃式的起跳，在起跳后一段时间驻室压力稳定之后脉动压力随之下降并在一个稳定平台内波动。比较来流前背景信号和脉动信号可以发现，有效试验时间内的脉动信号远大于背景噪声。结合图5的热流结果可知，6个PCB压力传感器在层流区域、转捩区域及全湍流区域均有布点，其有效时间段的脉动压力也呈现一定的变化规律。

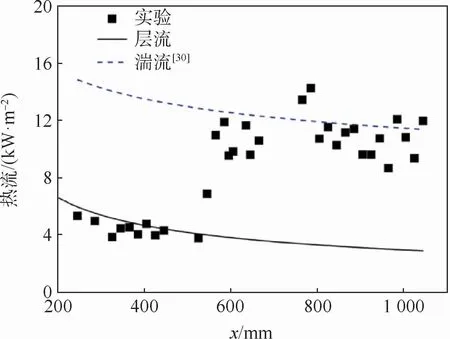
图5 尖锥母线热流分布Fig.5 Heat-flux distribution on sharp cone generatrix

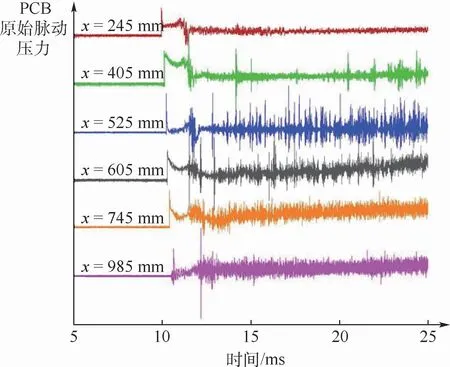
图6 不同位置PCB脉动压力信号Fig.6 Pressure fluctuation signals of PCB at different positions

功率谱（PSD）为单位频带内信号的功率，其能表示信号功率在频域内的分布状况，相关计算技术自提出以来获得了飞速发展，是研究信号频域特性最常用的方法之一。本文压力脉动的功率谱密度计算采用Welch法，由于PCB压力传感器有效的响应频率在11 k Hz以上，本文在对压力信号进行处理时利用巴特沃斯滤波器对信号进行了11 kHz的高通滤波，信号处理思路如图4所示。通过Welch方法计算脉动压力的功率谱，数据截取窗函数为50%交迭的汉宁窗，FFT分析长度为4 096，频率分辨率为427 Hz。另外，为了得到特定频率段的脉动信号，采用4阶巴特沃斯滤波器对原始信号进行高通和带通滤波处理。

本文实验状态下2次重复性实验同一位置传感器信号的功率谱如图7所示，其结果为405 mm位置处的PCB压力传感器。2次实验信号重复性较好，能量峰值及其所对应的频率吻合较好。虚线表示风洞未运行时的背景噪声，2次实验背景噪声同样较为吻合。在800 kHz以下频段有效脉动信号要远大于背景噪声信号，信号有足够高的信噪比，800 kHz以上后，有效信号基本上淹没在背景噪声里，本文为了分析方便，之后信号的功率谱分析只截取800 kHz以前的部分。

在边界层内，第二模态波传播速度与边界层外缘气流速度接近，波长近似为边界层厚度的2倍，第二模态波控制频率范围大致为100 k Hz～1 MHz［24］。图8给出了沿着模型子午线的PCB压力传感器脉动压力的功率谱分布。在第一个传感器（x=245 mm）处，脉动压力的功率谱随频率的增加呈指数式下降，200 kHz以上脉动压力已经下降到接近背景噪声的水平。位于405 mm处传感器测得的脉动压力在低频阶段下降之后随即迅速上升，在206 kHz处脉动压力达到峰值，并在354 kHz处出现其高次谐波。位于525 mm处的传感器测得的压力脉动峰值出现在177 kHz处，此时其高次谐波更加明显，中心频率为363 kHz。位于605 mm处的压力脉动峰值频率进一步下降到165 kHz。边界层厚度沿着模型流线方向不断增加，导致第二模态的频率不断下降。位于745 mm和985 mm处的压力脉动在各个频段已经没有了明显的峰值，边界层已经完成了转捩成湍流状态，脉动能量比较均匀地分布到各种频率波，且此时脉动能量要远高于第一个传感器处的情况。

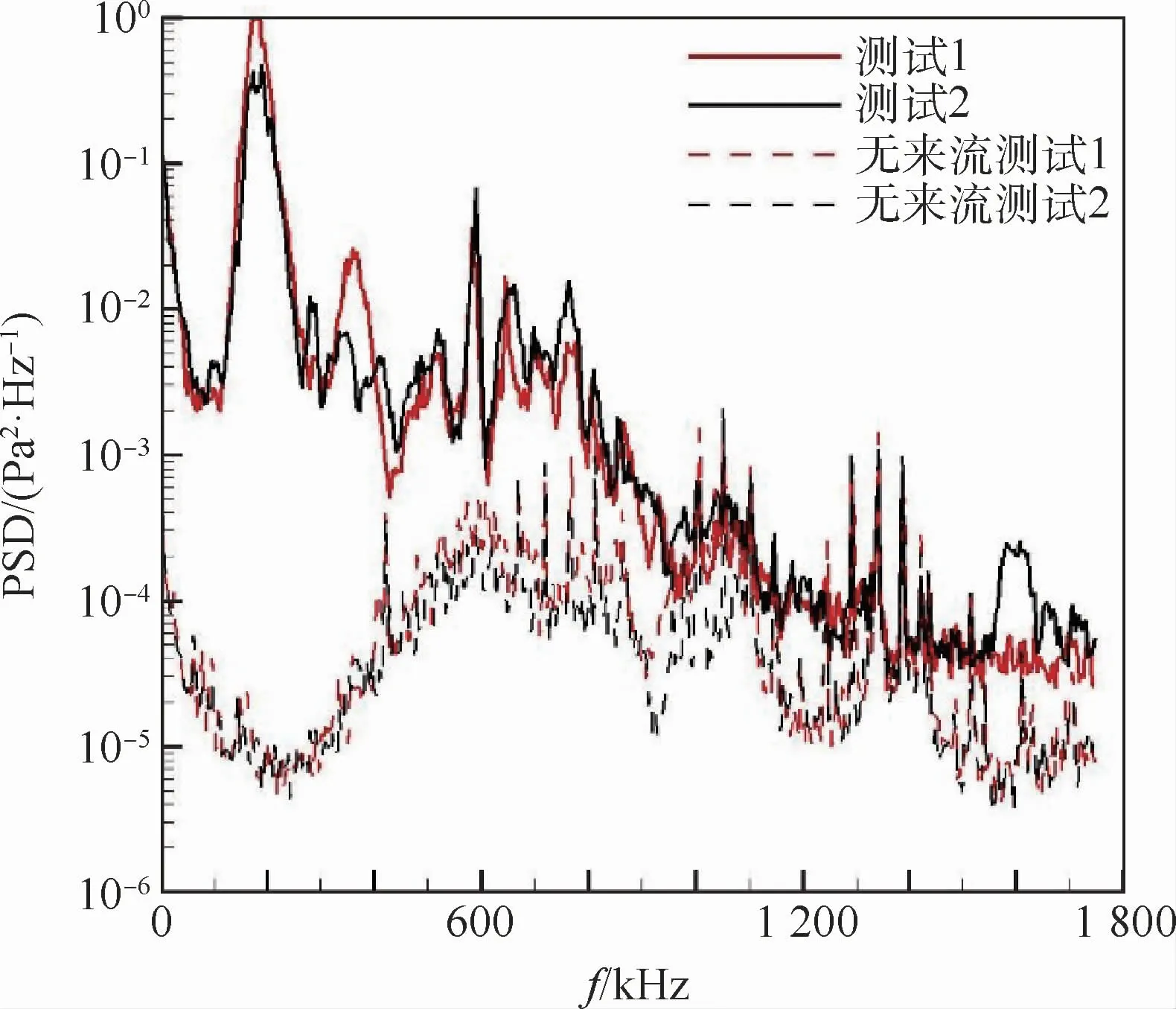
图7 典型脉动压力功率谱及背景噪声Fig.7 Typical fluctuation pressure PSD and background noise

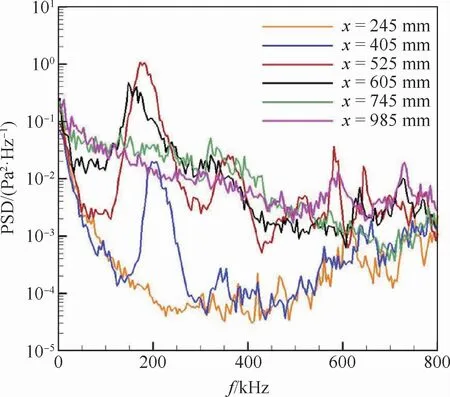
图8 模型子午线的功率谱结果Fig.8 PSD along model meridian

根据脉动压力的功率谱结果，单独对不同频段的脉动压力数据进行分析。图9（a）、（b）分别为利用带通滤波器单独滤出的11～50 kHz、150～250 kHz频段脉动压力信号，下游信号相对于上游处沿y轴移动了相同的距离。其中11～50 kHz对应第一模态波或第二模态的亚谐波可能出现的频率，150～250 kHz对应第二模态波出现的频率。在11～50 kHz频段，脉动压力在整个时间段内平稳分布，没有特定的波包出现。605 mm 以前的4个传感器压力幅度相当，但最后2个传感器在11～50 kHz的脉动压力幅值有明显提升。150～250 kHz频段第一个传感器脉动压力信号十分微弱，在405 mm处该频段内脉动压力开始增长，且间隙性地出现峰值。继续向下游发展时脉动压力出现明显的波包特性，脉动压力包络线中出现多个极值，此时第二模态扰动开始出现，到605 mm后脉动压力峰值达到最大，第二模态波迅速衰减的同时低频段脉动压力开始增加。

3 结 论

本文利用半锥角为7°的尖锥模型在JF8A激波风洞中开展了高超声速尖锥边界层的转捩实验研究，通过尖锥表面热流测量及PCB脉动压力测量分析了高超声速尖锥边界层中扰动波发展过程，主要结论如下：

1）JF8A激波风洞在雷诺数为6.4×106/m状态下核心流的自由流噪声为2.8%，喷管边界层内的噪声约为7.8%。

2）尖锥边界层在其转捩区有明显的第二模态稳定波出现，第二模态波频率随着边界层厚度的增加而减小；压力脉动度在层流区最小，在转捩结束位置压力脉动度会出现极大值。