采用固定点算法的局部放电特高频信号盲源分离方法
马鹏墀, 沈 盼, 王致杰
(1.上海电机学院 电气学院, 上海 201306; 2.江苏宏源电气有限责任公司 运维检修部, 江苏 南京 211100)
电力设备的绝缘性能劣化程度可以通过局部放电(Partial Discharge, PD)表现出来,同时PD会加剧绝缘劣化[1-2]。为了使电力设备安全可靠地运行,需要定期对电力设备进行局放检测[3-4]。但是由于现场电磁环境复杂,检测到的特高频(Ultra-high Frequency, UHF)PD信号会出现畸变,甚至湮没在干扰中,因此,需要对采集到的PD信号进行干扰抑制。
目前常用的去噪方法有小波分解法[5-6]、经验模态分解法[7-8]等。小波分解法受小波基的影响明显,若小波基选择不当会使PD波形出现畸变;而经验模态分解法会出现模态混叠的情况,影响去噪效果。现场的干扰主要是周期性窄带干扰和白噪声干扰,与局放信号无明显相关性,文献[9]利用这一特点,针对PD超声信号,基于相似矩阵的盲源分离(Blind Source Separation, BSS)法对PD超声信号中的干扰进行抑制。BSS能够在源信号特征未知的情况下将各种信号分离出来[10-11]。在含噪的UHF PD信号中,可以将白噪声干扰、周期性窄带干扰等噪声信号和PD信号都看作源信号,将未经处理的UHF PD信号看作观测信号,并利用BSS将各种源信号分离。
本文提出一种采用双树复小波变换(Dual-tree Complex Wavelet Transform, DTCWT)和固定点算法(FastICA)进行UHF PD信号BSS的方法,先利用S变换进行源信号数量估计,再通过DTCWT对源信号进行分解,得到虚拟的多通道信号并重组,最后采用FastICA算法进行BSS,得到不含噪声的UHF PD信号。
1 BSS去噪原理
1.1 BSS的数学模型
现场采集的UHF PD信号通常含有白噪声干扰信号和周期性窄带干扰信号。其中,PD信号为暂态非平稳信号,白噪声为随机干扰信号,窄带干扰为平稳的周期信号,各种信号互不相关,满足独立性要求[12],且属于线性混合模型[13]:
x(t)=As(t)
(1)
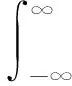
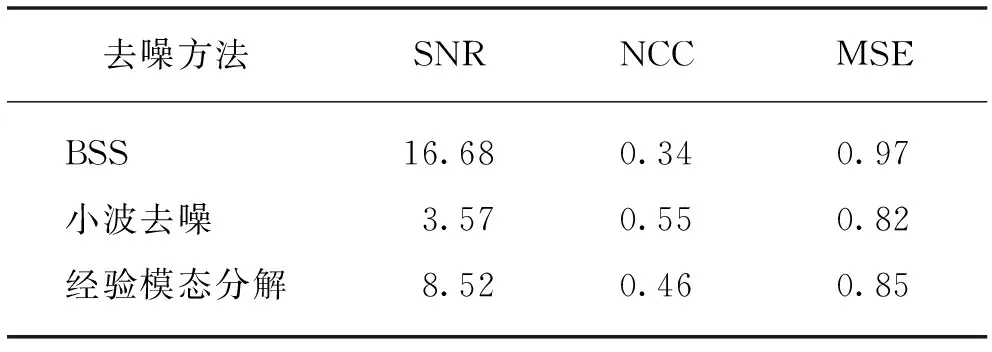
式中:x(t)=[x1(t),x2(t),…,xM(t)]T是由M个传感器获取的观测矢量构成的观测信号矩阵;s(t)=[s1(t),s2(t),…,sN(t)]T是由N个未知独立信号组成的源信号矩阵;A为混合矩阵。当M 图1所示为BSS原理,BSS的本质是找到分离矩阵W,从x(t)中分离出s(t),并获取最优输出信号矢量为 图1 BSS原理 y(t)=Wx(t) (2) 对UHF信号进行时频分析可以确定源信号的数量,现场获取的UHF信号是时域信号,利用S变换可以将其转换至时频域内。S变换结合了傅里叶变换和小波变换的优点,其定义如下: (3) 式中:f为频率;ω(t-τ,f)为高斯窗函数,表达式为 (4) 根据S变换得到的时频矩阵可以绘制出x(t)的三维时频图谱,可反映各类信号的时频特征。PD信号频率高,持续时间短;白噪声无明显规律,离散分布;周期性窄带干扰具有周期性,持续时间长且频带窄。根据以上特征可以确定信号源的数量。 DTCWT利用两组滤波器对输入信号进行滤波,得到实部和虚部两个小数波。实部滤波器h0(m)、h1(m)和虚部滤波器g0(n)、g1(n)对应的尺度函数φ(t)和小波函数ψ(t)如下: (5) 最终得到的双树复小波函数为 ψ(t)=ψh(t)+jψg(t) (6) 式中:ψg(t)=H[ψh(t)],H[·]为希尔伯特算子。 FastICA算法按照迭代原理向最大负熵方向寻求目标信号,是独立分量分析ICA演变而来的一种快速信号分离算法。利用FastICA算法寻找分离矩阵W,W=[w1,w2,…,wm]T,使Y=Wx方向有最大非高斯量。若利用负熵衡量非高斯变量,设负熵为Ng(Y),则 Ng(Y)=H(YGauss)-H(Y) (7) 式中:YGauss为高斯变量且等于Y的方差,H(·)为Y的微分熵,即 (8) 式中:py(x)为概率密度。 负熵Ng(Y)与非高斯量成正比,因此,可以用负熵表示随机变量的非高斯量。通常用负熵近似衡量非高斯量,近似公式为 J(y)∝(E[G(y)]-E[G(v)])2 (9) 式中:E[·]为数学期望;G为非线性函数。 对式(9)进行拉格朗日变换后得到的等价函数为 (10) 用牛顿-拉夫逊法求式(10)的最大值,迭代公式为 (11) 图2所示为利用FastICA算法对信号进行分离的具体流程。 图2 FastICA算法信号分离流程 为了验证基于DTCWT和FastICA的BSS方法对UHF PD信号的去噪效果,在实验室模拟4种典型PD缺陷[15],试验电压如表1所示,通过图3的试验平台获取UHF波形。其中,T1为调压器,T2为无晕试验变压器,R为保护电阻,C1和C2为工频分压器。示波器的型号为LeCroy8254,带宽为2.5 GHz,最大采样率为20 GSa/s。通过试验获取的4种放电缺陷的UHF波形如图4(a)所示,加入白噪声干扰和周期性窄带干扰后的结果如图4(b)所示。由于常见的窄带干扰有手机信号,频率为900 MHz或1.8 GHz等,因此,窄带干扰可以通过如下数学模型表示: 图3 试验平台 图4 试验用UHF PD波形 表1 4种放电类型对应的试验电压 (12) 式中:Z1(t)、Z2(t)分别为表示频率为900 MHz或1.8 GHz时的函数模型;A、B一般取0.005。 将本文的BSS方法与小波去噪和经验模态分解去噪方法进行对比,3种方法的去噪结果如图5所示。 图5 3种方法去噪后的PD波形 引入信噪比、波形相似参数和均方误差3个指标对去噪效果进行评估[16]。 (13) (14) (15) 信噪比越大,说明去噪效果越好;波形相似参数越小,说明波形畸变程度越低;均方误差越接近1,说明去噪前后波形相似度越高。对3种去噪方法评估后的结果如表2所示。 表2 3种方法的评估参数 对图5和表2的结果进行分析,得出以下结论:① 小波分解的去噪效果受小波基选择的影响明显,而现场PD信号复杂多变,选择合适的小波基十分困难,导致去噪后的波形出现畸变,第2个PD信号也被去除;② 由于一些窄带干扰信号的频率与PD信号的频率重合,导致经验模态分解法不能完全去除周期性窄带干扰,去噪后的PD信号仍含有干扰信号;③ 利用基于DTCWT和FsatICA的BSS法对UHF PD信号进行去噪,弥补了上述方法的不足,获取了较为完整的PD波形。 本次带电检测采用的示波器型号为DSO-X3104T,带宽为1 GHz,最大采样率可达1 GSa/s,现场PD信号的去噪结果如图6所示。由于现场存在大量干扰,因此采集到的信号信噪比低。对于现场检测的PD信号,由于无法直接获取未染噪的原始PD波形,因此,无法评估波形相似度,但可利用噪声抑制比来评估去噪能力,反映去噪前后信号的凸显程度,定义如下: 图6 现场PD信号的去噪结果 (16) 为了提升PD信号的去噪效果,根据小波变换和经验模态分解的优缺点,提出一种利用DTCWT和FastICA进行PD盲源分离的去噪方法。通过对仿真实验和现场实测的UHF PD信号进行去噪,验证了该方法的有效性,并得出以下结论: (1)现场采集的PD信号属于极端欠定情况,利用分离矩阵W可以将单通道采集的PD信号分解为多信号,能够很好地解决PD信号盲源分离过程中的欠定问题。 (2)本文提出的PD信号去噪方法可以有效地抑制现场常见的白噪声干扰和周期性窄带干扰,且不会使PD波形发生畸变,具有良好的去噪效果。
1.2 源信号的数量估计
1.3 DTCWT多通道源信号重组
1.4 FastICA算法BSS去噪


2 实验分析
2.1 模拟UHF PD信号的获取



2.2 去噪效果及分析

3 现场PD信号验证

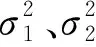
4 结 论

