基于WOA-LSSVM算法的风机齿轮箱故障诊断
郑坤鹏, 丁云飞
(上海电机学院 电气学院, 上海 201306)
随着风电产业的发展,风力发电机组的稳定安全运行日益重要[1]。齿轮箱是风力发电机组的一个重要组成部件,对其进行精确的故障诊断对风力发电机组的稳定运行至关重要[2]。传统对齿轮箱振动信号处理的方法多为小波分析法[3],经验模态分解法等。集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)法通过对原信号加入白噪声的方式,对模态混叠有一定的抑制效果[4-5]。但是由于EEMD算法迭代次数较多,增加了计算量,而且分量未必都能具有物理意义,出现较多无意义的本征模态函数(Intrinsic Mode Function, IMF)分量,不利于后续风机齿轮箱故障的提取。郑近德等[6]提出了改进的集合经验模态分解法(Modified EEMD, MEEMD),在一定程度上解决了上述问题。
随着人工智能技术的发展,利用智能算法实现机械故障诊断是一个趋势,经典的分类算法有神经网络、支持向量机、决策树等。其中,支持向量机由于其算法简单,所需样本少等特点应用最为广泛。支持向量机虽然可以取得较好的分类效果,但是当其处理数据量较大的样本数据时,其计算效率低,正则化参数和核函数参数选择也较为困难,很可能会导致分类的效果不佳。本文采用计算效率更高的最小二乘支持向量机(Least Squares Support Vector Machines, LSSVM)和新近提出的鲸鱼优化算法(Whale Optimization Algorithm, WOA)相结合,建立WOA-LSSVM齿轮箱故障诊断模型,对上述基于MEEMD和样本熵的故障特征进行训练测试,实现故障诊断。通过实验对比,验证了该风机齿轮箱故障诊断模型的有效性。
1 诊断算法原理
1.1 MEEMD算法理论
MEEMD引入了信号分析中排列熵这个概念,排列熵具有检测时间序列随机性的功能,其大小可以反映信号序列的随机性[7]。MEEMD的基本原理是,通过计算排列熵对分解信号进行复杂度评价,排列熵的取值范围为0~1,数值越大,信号复杂度越大,把复杂度过大的信号视为异常信号,把异常信号从原始信号中去除,最后对剩余的信号再进行EMD分解,即得到MEEMD的分解结果。
1.2 样本熵
样本熵是由Richman等[8]提出的一种时间序列复杂性的度量方法。样本熵数值越低,时间序列的复杂度就越低;数值越大,时间序列复杂度就越高。样本熵是对近似熵的改进,与近似熵算法相比具有抗噪声干扰强、精度高、一致性好等优点,不依赖于数据的长度,可以作为风机齿轮箱的故障特征[9]。
1.3 LSSVM原理
LSSVM分类算法与传统的支持向量机相比,目标函数由不等式约束变为了等式约束,大大简化了计算的复杂度[10-11]。实验证明,LSSVM算法在模型的复杂度和训练结果精确度之间取得了很好的平衡,更适合数据样本复杂的情形。LSSVM算法的实现流程如下:
设l个样本数据(xi,yi)对应的类别yi∈{-1,1},LSSVM回归函数形式为
y=w·φ(x)+b
(1)
式中:w为超平面的法向量;b为偏置量,是一个常数;xi为输入量;yi为模型输出量;φ(x)为映射函数,可以把输入量从低维映射到高维空间。
LSSVM的优化数学模型为
(2)
式中:ei为误差;γ为正则化参数。
对式(2)引入拉格朗日乘子ai,建立拉格朗日方程。上述优化问题转化为最小值问题,有
minL(w,b,e,a)=
(3)
由拉格朗日乘子法取得最值的条件得:
(4)
此时,LSSVM的回归表达式为
(5)
(6)
式中:K(xi,xj)为选择的径向基核函数;σ为径向基核函数的参数,其数值影响LSSVM模型的核函数的映射能力。
1.4 WOA
WOA属于群体智能优化算法,通过模拟鲸鱼的捕食过程建立数学模型[12]。鲸鱼是一种群居的哺乳动物,在捕猎时它们也会相互合作对猎物进行驱赶和围捕。当鲸鱼在海底发现猎物时,会以螺旋环状向上的路径制造出泡泡网,并且通过不断地收缩泡泡网,渐渐地将鱼虾包围聚集,最终完成捕食。该鲸鱼的捕食过程总结为:包围猎物、气泡攻击、搜寻猎物[13]。
WOA基本步骤如下:
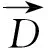
(7)


(8)
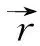
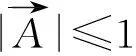
(2)气泡攻击。鲸鱼优化算法中,设置了两种鲸鱼捕食方式,分别为收缩围捕方式和螺旋泡泡网攻击方式。
螺旋气泡网攻击方式:鲸鱼个体以螺旋路径的方式,对猎物进行捕食。采用的更新位置方程为
(9)

为了模拟鲸鱼群体对猎物攻击时,同时使用收缩包围和螺旋路径的方式,WOA设置了一个概率p,p为[0,1]之间的随机数,假设鲸鱼分别采用两种捕食方式的概率皆为0.5,则鲸鱼位置迭代数学模型为
(10)
(11)

WOA的伪代码如下:
初始化下列参数:
鲸鱼种群Xi(i=1,2,…,N)
空间维度——dim
最大迭代次数——Tmax
适应度函数
计算适应度函数最优时对应的鲸鱼个体X*
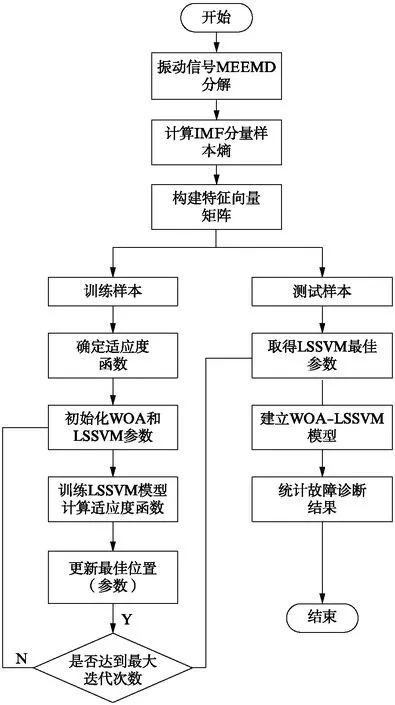
while(t fori=1:N 更新参数a,A,p,C,l if 1(p<0.5) if 2(|A|≥1) 采用式(11)更新鲸鱼位置 else if 2(|A|<1) 采用式(7)更新位置 end if 2 else if 1(p≥0.5) 采用式(9)更新鲸鱼位置 end if 1 end 检查鲸鱼位置是否越界并修正位置 计算鲸鱼适应度值,确定是否更新最优鲸鱼位置X* t=t+1 end while 1.2.2观察组采用方法 本组研究对象采取CTA检测,检测方法:选择64层螺旋CT扫描系统进行检测,于患者肘正中静脉将非离子型对比剂注入,剂量为2mg/kg,注入速度为每秒3~4ml,延迟时间为15秒~23秒。扫描参数:300mA、120kV、螺距为3.5、层厚为1mm、重建间隔为0.5mm。 returnX* 由LSSVM算法的基本原理可知,获取合适的参数对LSSVM模型至关重要。 LSSVM具有两个参数:正则化参数γ和核函数参数σ,这两个参数对LSSVM分类模型影响巨大[14]。一些经典的智能优化算法经常用来优化LSSVM模型,如粒子群优化(PSO)算法、遗传算法(GA)等[15]。虽然上述算法对于LSSVM的分类效果具有一定的提升,但是却不容易跳出局部极值的陷阱,导致分类精度不高,WOA与这些算法相比具有运算简单快速、全局搜索能力强等优点,有很大的概率摆脱局部极值。因此,本文采用WOA优化LSSVM的两个参数,建立了WOA-LSSVM风机齿轮箱故障诊断模型,实现流程如图1所示。 图1 WOA-LSSVM故障诊断模型 依据上海电气集团的故障诊断平台,设定采样频率为2 000×2.56 Hz,通过加速度传感器采集在转速880 r/min、加载电流0.05 A情况下的正常、断齿、磨损、点蚀4种振动信号。对信号进行预处理,得到风机齿轮箱4种状态下的振动信号各25组,一共100组信号。 以断齿故障振动信号为例,完成其故障特征向量的构建,如图2所示,其中纵坐标a为振动信号加速度。 图2 齿轮箱原始信号 振动信号MEEMD分解结果如图3所示。 图3 断齿信号MEEMD的分解分量 选择前6个IMF分量计算样本熵组成特征向量: (12) 按照上述方法提取100组样本数据的故障特征向量,可组成样本个数为100的样本集。 为了验证WOA-LSSVM风机齿轮箱故障诊断模型的优越性,设置仿真对比实验流程如下: (1)随机选取4种状态下的齿轮箱故障样本:正常、断齿、磨损、点蚀各5组,一共20组作为训练样本集。剩余的80组样本作为测试样本,其中4种故障类型各20组。 (2)基于上述理论与方法,分别建立LSSVM、遗传算法优化的最小二乘支持向量机(GA-LSSVM)、粒子群优化的最小二乘支持向量机(PSO-LSSVM)、鲸鱼算法优化的最小二乘支持向量机(WOA-LSSVM)4种未经训练的故障诊断模型。 (3)对20组训练样本分别输入4种故障诊断模型,对模型进行训练,得到训练后的模型。 (4)对80组测试样本分别输入训练完成的LSSVM、GA-LSSVM、PSO-LSSVM、WOA-LSSVM 4种风机齿轮箱故障诊断模型,得到具体分类结果后,统计各自的故障识别率。 统计基于LSSVM、PSO-LSSVM、GA-LSSVM、WOA-LSSVM 4种算法的风机齿轮箱的故障诊断结果如图4所示。 图4 4种故障诊断模型混叠矩阵 由图4可知,LSSVM的故障诊断模型表现最差,误分类个数为6个;PSO-LSSVM和GA-LSSVM两种故障诊断模型由于陷入了局部极值,误分类个数分别为5和4,均不能取得较好的分类效果;WOA-LSSVM算法的分类表现最好,4种故障全部分类正确。 由此可知,WOA与GA和PSO算法相比,更易跳出局部极值,3种优化模型的适应度曲线如图5所示。 图5 3种优化模型适应度曲线 由图5可知,随着迭代次数的增加,WOA的全局搜索能力逐渐显现,不断跳出局部极值直到适应度取得最大值;与WOA相比,PSO算法与GA的适应度(故障准确率)曲线为一条直线,均不能跳出局部极值。实验表明,基于WOA-LSSVM算法的风机齿轮箱故障诊断模型,在故障识别方面表现更加优异。 本文将MEEMD分解算法与样本熵结合提取风机齿轮箱的故障特征,并且采用WOA对LSSVM参数进行选择,与经典的GA和PSO算法对比,验证了WOA具有更好的全局搜索能力,建立了WOA-LSSVM风机齿轮箱故障诊断模型。通过实验对比分析验证了WOA-LSSVM算法的有效性以及优势,对风机齿轮箱的故障诊断具有一定的指导意义。2 WOA-LSSVM风机齿轮箱故障诊断模型
3 实验分析
3.1 实验数据来源与故障特征提取
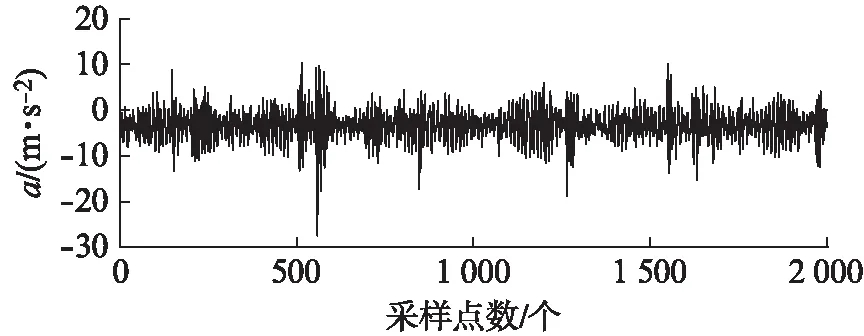
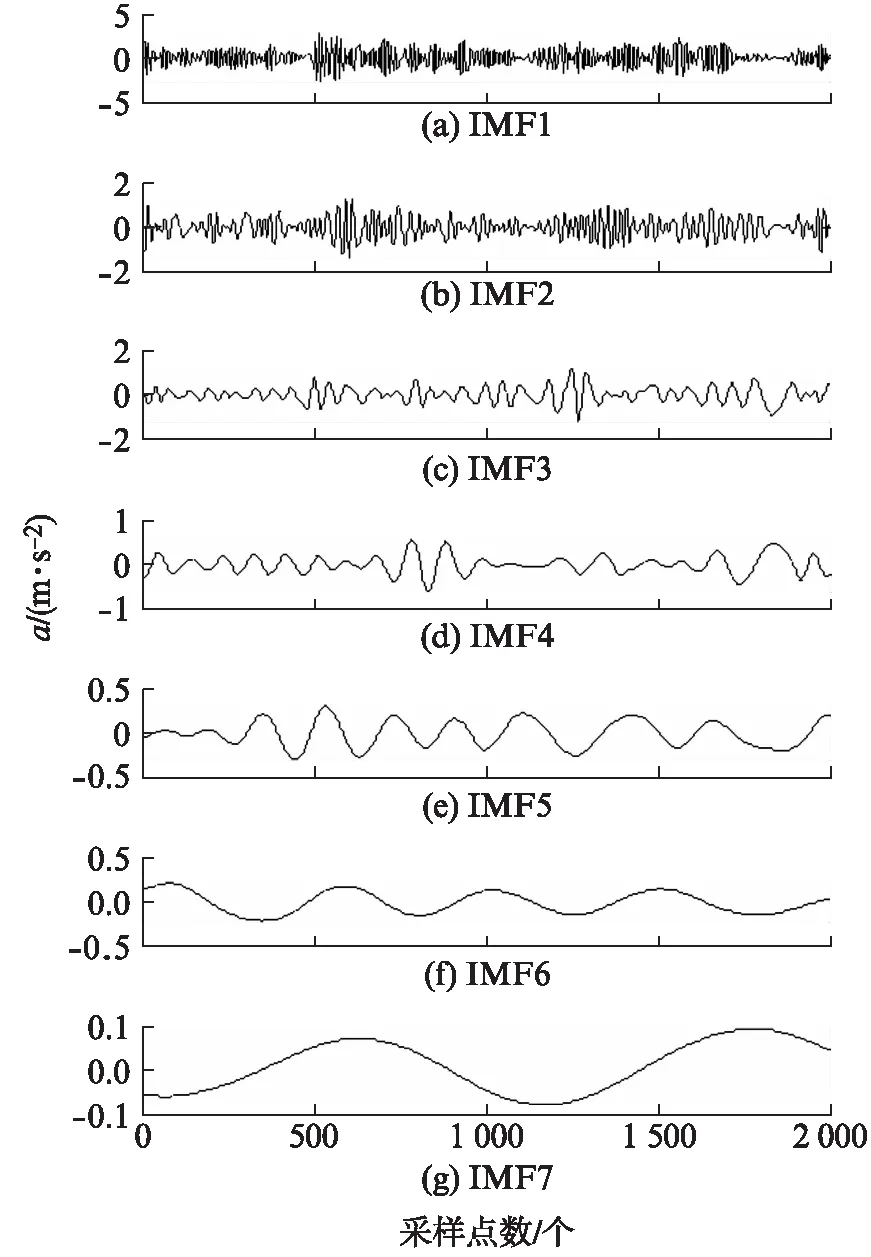
3.2 实验过程及结果分析


4 结 论

