基于回归分析的人脸年龄预测研究
张 德, 哈 曼
(北京建筑大学 电气与信息工程学院&建筑大数据智能处理方法研究北京市重点实验室, 北京 100044)
人脸图像包含了许多重要信息,如性别、种族、年龄、身份、表情以及头部姿态等各种可感知信息。与人脸图像紧密相关的分析处理和识别估计等技术已经发展为计算机视觉和模式识别等技术领域的重要研究课题。人脸年龄预测是其中的一个主要研究方向,指从包含有人脸的图像中判断和估计该人脸相应的年龄。基于人脸图像的自动年龄预测在人机交互、未成年人身份信息识别以及安全监控等信息技术领域中都具有广阔的应用和研究前景[1-2]。
基于人脸图像的年龄预测或者估计问题一般通过对人脸图像特征随着年龄变化的规律进行建模来解决,可以使用统计学习或者机器学习的方法进行建模。然后基于建立的模型,计算机或者计算机类的机器能够计算和推测出人的大概年龄或所属的年龄范围。年龄预测属于比较特殊的模式识别问题,有2个方面的原因。其一,每个年龄值可以是一个类别,所以年龄预测可以被看作分类问题去研究;其二,由于年龄的增长是一个数列的有序变化过程,所以也可以被看作回归问题。
与人脸识别、表情识别等人脸图像相关研究比较,人脸年龄预测研究起步较晚,但近年来,逐年呈现上升趋势。在分类模式方面,朱明等[3]提出一种基于改进混合蛙跳算法的支持向量机(Support Vector Machine,SVM)训练算法,用于人脸年龄的分类;赵军等[4]把字典学习应用于年龄分类,从人脸区域提取主要特征和次要特征,并分别进行训练,提出了一种加权字典对学习的年龄估计方法;梁晓曦等[5]同时考虑了人脸的全局特征和关键局部特征,使用神经网络方法进行年龄分类。在回归模式方面,曾雪强等[6]使用标准差自适应生成不同标准差的年龄离散高斯分布,然后使用偏最小二乘回归建立人脸年龄预测的回归模型;房国志等[7]通过结合多尺度特征回归和卷积神经网络,并训练和构造决策树进行人脸年龄预测,也可以基于分类和回归混合模型进行人脸年龄估计;赵一丁等[8]提出年龄段重叠区域的思路,并针对不同的年龄段分别使用分类或者回归模型,然后在重叠区域进行均值融合,取得了较低的年龄预测误差。
考虑到支持向量机在分类方面有很好的优势和应用,后来被推广到用于解决回归问题,在小样本的情况下支持向量机不仅算法简单,而且具有较好的鲁棒性[9]。另外,对于年龄估计研究而言,由于难以获得同一个人从出生到少年、青年,再到中年、老年时期的人脸图像,人脸年龄数据库规模相对来说比较小。因此,本文使用支持向量机进行回归分析,设计和完成了人脸年龄预测的实验,并跟经典的回归模型进行比较。实验结果表明基于支持向量机回归的年龄预测更为准确。
1 人脸年龄预测系统
使用回归分析的方式实现基于人脸图像的年龄预测,一般分为4个步骤:人脸图像预处理、特征提取、训练回归模型和输出预测年龄。依据选用的特征提取方法和回归方法,给出本文进行基于人脸图像的年龄预测流程,如图1所示。
接下来分别介绍图1中提到的各个步骤。首先是人脸图像预处理,数据库中的人脸图像需经过标准的预处理操作,包括人脸几何归一化和灰度归一化操作。几何归一化包括裁剪人脸区域、校正人脸的方向和统一人脸图像区域的大小,让人脸处于水平的状态。灰度归一化通过增强图像的对比度,进行光照补偿,让人脸图像处于同样的环境状态。然后,使用主成分分析(Principal Component Analysis,PCA)方法进行特征提取,降低人脸图像数据的维数。PCA方法经常用于减少数据特征的维数,同时还可以最大限度地保留原数据的信息,对训练数据和测试数据需要使用同样的特征提取方法。接下来,基于提取的训练图像的PCA特征数据,使用支持向量机回归方法进行模型训练,生成可用于年龄预测的回归模型。最后,把模型应用到来自不同测试图像的PCA特征数据上,输出人脸对应的年龄。
1.1 人脸图像预处理
人脸图像预处理主要包括几何归一化和灰度归一化2种操作,如果数据库中包含一些彩色图像,需要先把它们转换为灰度图像。几何归一化具体包括4个步骤:
1)标定特征点,通过鼠标点击获取左右两眼的中心坐标值。
2)根据左右两眼特征点的标定,旋转人脸图像,保证双眼连接线处于水平方向。
3)基于两眼之间的水平距离,根据面部几何模型比例确定人脸矩形区域并裁剪。
4)把截取的人脸区域图像尺寸变换到统一大小,长和宽可以都设一个固定值,然后以双线性插值的方法实现。
灰度归一化主要是通过增加图像的亮度和对比度,使图像的细节更加清楚,减弱光照强度的影响。灰度归一化操作可以通过图像直方图均衡化方法实现。本文使用的人脸年龄图像数据库是FG- NET,来自该数据库的示例图片和相应的预处理结果如图2所示。
由图2可以看出,经过预处理操作,数据库中的图像原有的客观性差异变小,能够以一致的姿态和均衡的亮度条件进行后续的特征提取处理,从而提高系统的稳定性。
1.2 特征提取
经过预处理之后的人脸图像数据维数仍比较大,这里选择使用PCA方法进行特征提取和降维,PCA同时还可以起到相关性去除的作用。PCA是以Karhunen-Loeve(K-L)变换为基础,通过解除原有数据向量的各个分量之间的相关性,可以消除带有很少数据特征信息的坐标分量,以达到降低特征空间维数的目的。
为说明PCA方法的计算过程,假设归一化后的图像大小是mn,m和n分别表示图像的行数和列数,按列相连可构成N维列向量:
N=mn
(1)
然后以xi表示第i个图像样本向量,每个xi都是N维列向量。设训练样本数为M,则组成大小为NM的样本矩阵X:
X=[x1,x2,…,xi,…,xM]
(2)
每个图像样本xi可看作N维空间中的1个点,接下来通过K-L变换生成1个低维子空间来描述每个样本,新的特征空间投影矩阵计算步骤如下所述。
步骤1:计算训练样本的平均向量mX:
mX=(x1+x2+…+xi+…+xM)/M
(3)
然后,每个训练样本向量减去该均值,结果以φi表示:
φi=xi-mX
(4)
得到新的矩阵A:
A=[φ1,φ2,…,φi,…,φM]
(5)
步骤2:计算协方差矩阵CA:
CA=(AAT)/M
(6)
新的坐标系由矩阵CA的非零特征值对应的特征向量组成。由于样本特征维数较高,直接求AAT的特征值和特征向量很困难,所以转而求解矩阵ATA的特征值和特征向量。

(7)
正交归一特征向量ui为:
(8)
步骤4:把CA的非零特征值按照从大到小排序为[γ1,γ2,…,γi,…,γr],其中1≤r Y=UTxi(Y∈Rr) (9) 利用以上得到的特征空间矩阵U,首先把所有训练样本图像进行投影,然后对测试样本也进行同样的投影,得到的投影系数就是降维之后的PCA特征。 支持向量机回归(Support Vector Regression, SVR)是支持向量机中的一个重要应用分支。SVM是一种常用的分类算法,也可以用于回归。SVR与SVM的区别在于,SVM使到超平面最近的样本点的距离最大,SVR是使到超平面最远的样本点的距离最小,超平面的划分可由法向量w和位移b确定。 对于SVR回归问题,给定训练数据D为: D={(x1,y1),(x2,y2),…,(xi,yi),…,(xM,yM)} (10) 式中,xi表示数据样本,yi表示样本的输出标记。 目标是建立一个回归模型f(x)=wTx+b,确定最合适的超平面,使得f(x)和输出标记y尽可能接近。传统的回归模型基于当且仅当f(x)和y完全一样时,模型输出f(x)的损失才为0。而SVR则定义一个误差常量ε,只要f(x)和y的偏离程度不超过ε,即可认为模型预测准确。因此,SVR只是计算|f(x)-y|>ε的数据点的损失,损失函数lε为: (11) 然后,SVR的目标函数为: (12) 式中,C为正则化常数。 SVR回归模型和SVM分类模型相似,也对每个样本(xi,yi)加入松弛变量,定义为ξi和i,将式(12)优化为: (13) 其中,松弛变量ξi和i需满足条件:f(xi)-yi≤ε+ξi,yi-f(xi)≤ε+i,ξi≥0,i≥0,i=1,2,…,M。 使用拉格朗日函数把目标优化函数式(13)变成无约束的形式: L(w,b,α,,ξ,,μ,)= (14) 式中:αi≥0、i≥0、μi≥0、i≥0是拉格朗日乘子。 式(14)对w求偏导,并令偏导为0,得到: (15) 然后,转化为等价的对偶问题来求解,SVR的解f(x)为: (16) 另外,支持向量机中有大量的核函数可以使用,用于解决各种非线性数据的分类回归问题。核函数的扩展也比较简单,只需要把x用核函数φ(x)代替,得到的回归模型为: (17) 本文的实验选用了人脸年龄估计研究中常用的数据库FG-NET,该数据库包含来自82个人的人脸图像,共计1 002张,所对应的年龄分布在0~69岁。为了充分利用数据库中的样本图像,选用留一校验法,每次使用1个人的图像样本作为测试集,剩下的所有图像样本为训练集。这样,一共需要循环82次,取所有结果的平均值作为最终的年龄估计误差。为了评估本文所使用年龄预测方法的性能,选用2个常用的评价指标对实验结果进行评估。一个是平均绝对误差(Mean Absolute Error, MAE),另一个是累计分数(Cumulative Score, CS)。MAE表示误差,值越小说明算法性能越好。CS表示年龄估计误差在某范围内(可以取3~10岁的数)的所有样本占总样本的比例,显然,CS值越大说明算法性能越好。 FG-NET数据库中40岁以上的人脸图像样本较少,所以划分了5个年龄段进行结果评估,分别是0~9岁、10~19岁、20~29岁、30~39岁和40~69岁。PCA降维选取累积能量占前90%的特征维数,提取的特征数据为88维。SVR训练回归模型选用径向基核函数(Radial Basis Function, RBF),然后进行年龄预测实验。不同年龄段的年龄估计结果评价比较见表1。 表1 不同年龄段的年龄估计结果评价比较 从表1可以看出,0~9岁和10~19岁年龄段的平均绝对误差(MAE)较小,而且各个累积分数(CS)的结果也相对较高。30~39岁和40~69岁年龄段的平均绝对误差较大,各个累积分数的值也相对较小。结合样本数量所占比例的分析,由于这2个年龄段的样本图像数量偏少,得到的训练模型在该年龄段预测的结果就比较差,所以误差比较大。另一方面,由于人脸年龄生理变化的影响,不同年龄阶段的人脸老化程度和速度不一样,也会影响年龄预测的结果。 为验证支持向量机回归模型的有效性,进行了一元函数回归、二元函数回归以及多重多元回归方法的比较实验,表2列出了这几种不同的回归方法得出的年龄估计误差,以MAE进行评估。 表2 不同回归方法的MAE结果比较 由表2可知,本文使用的SVR得出的平均绝对误差最小,所以实验取得了预期的效果。同时,从表2也可以看出,在不同的回归算法下,较大年龄段情况下的MAE比较高,和表1给出的变化趋势一致。图3给出了部分样本图像的真实年龄和预测年龄对比,表明使用PCA特征提取方法和SVR回归模型可以进行较好的年龄预测。从图3中可以看出,所选取的样本示例年龄阶段包含了幼年、少年、青年和中年时期,真实年龄和预测年龄之间的差异都不大。为进一步验证本文方法的可靠性,对来自网络的一些明星人物的人脸图片进行了年龄预测,如图4所示。虽然在训练集中不包含这些人物的不同年龄段的样本图像,但是从图4中可以看出,对于中青年的实际样本示例,真实年龄和预测年龄之间的差异在可以接受的范围内。不过,对于真实年龄为51岁的样本预测差异比较大,后期还需要进一步提高中老年阶段的年龄预测准确度。 本文进行了基于人脸图像的年龄预测研究,采用主成分分析法提取人脸特征,然后使用支持向量机回归的方法进行训练和测试,在公开的FG-NET人脸图像数据库上进行了实验。通过MAE和CS 2种评价指标的分析,结果表明取得了良好的年龄估计结果,并给出了部分样本的真实年龄和预测年龄的对比示例,也对一些实际的人脸图片进行了年龄预测的验证。通过和其他回归方法的比较,展现了支持向量机回归方法的优势,可以获得更低的年龄预测误差。本文得到的实验结果说明基于人脸图像的年龄预测是可行的和可靠的,可以应用在智能安防中的人脸属性判别、商业中的受众人群数据分析和智慧医疗等方面。由于当前使用的人脸数据库中图像背景比较单一,后续的研究工作会更多关注非限制场景或者多种头部姿态条件下的人脸年龄预测问题。1.3 支持向量机回归
2 实验和比较
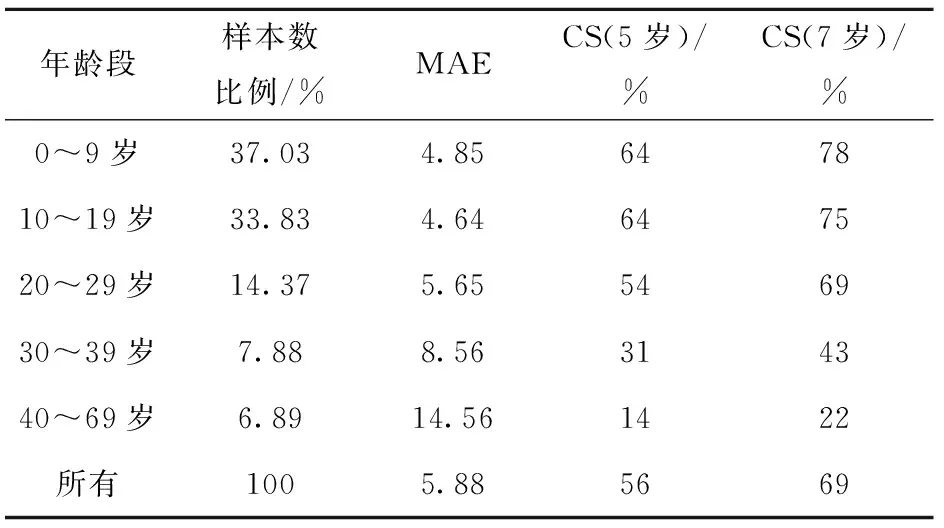
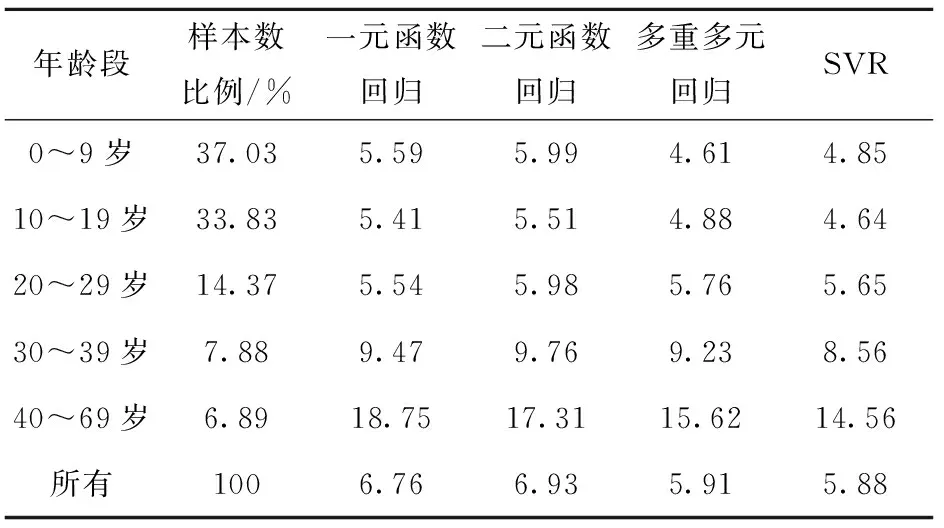
3 结论

